Datová hranice

Ve druhé části čtyřdílné volně navazující studie časových systémů je ústředním tématem datová hranice. Ta je přímým důsledkem mapování (značkování) času probraném v první části a přináší celou řadu nečekaně zajímavých situací i časových paradoxů. Je na jedné straně kostlivcem, ale na druhé opravářem zvoleného matematického řešení při konstrukci časového systému na základě pohybu Slunce po obloze. Článek začíná záhadou, která vznikla na dávných námořních výpravách a jejím řešením. Pokračuje dál rozborem formalizmu vzniku dní v jednotlivých časových pásmech, včetně pohybu těchto „časových ploch“ v prostoru a čase. V závěru článku je na konkrétním příkladu letu letadla kolem Země ilustrována jak funkčnost zvoleného matematického řešení, tak i jisté potíže s tím spojené.

Pomalé cestování kolem Země a vznik datové hranice

Kde se vzala nějaká mezinárodní datová hranice? Potřebujeme vůbec něco takového? A nemůžeme ji zrušit? Čí to byl nápad? Nejlepší bude se nejdříve vrátit zpět do historie k prvním námořním výpravám.

Historicky se uvedený problém s datovou hranicí týkal především námořníků. Přesto, že si v průběhu první výpravy kolem Země směrem na západ posádka Magellanovy výpravy vedla na lodi svůj deník velmi pečlivě, stejně jim nakonec při srovnání s kalendářem na pevné zemi jeden den v deníku chyběl. A k podobným nesrovnalostem s kalendářem docházeli na svých plavbách později i jiní námořníci. Vznikla otázka, kde vlastně mizí den, když si každý nový den pečlivě zaznamenávali do svého lodního deníku. Odpověď spočívá ve způsobu měření času, který se sice v průběhu staletí zdokonalil a zpřesnil, ale jeho podstata se dodnes nezměnila. Systém přiřazování časových souřadnic jednotlivým bodům povrchu Země zůstal.

V dávných dobách lodě pluly po moři velmi pomalu, například Magellanovi trvala cesta kolem světa víc než tři roky (1519 – 1522). V takovém případě dochází k nepozorovatelné změně počtu oběhů Slunce kolem lodi („lodních dnů“), měřených námořníky přímo na svých plavidlech, ve srovnání s počtem oběhů Slunce vůči pevnému povrchu Země, tj. „skutečných dnů“. Námořníci si na lodích dny měřili sami podle východů a západů Slunce, ne podle atomových nebo jiných centrálních hodin.

Pokud námořník pluje směrem na západ, otáčení, změna úhlu mezi lodí a Sluncem (rotace) se bude nepatrně zpomalovat a dny cestovatele budou nepatrně delší než dny na pevné zemi (zde „nepohybujícím“ se moři). Po obeplutí celé zeměkoule uplyne na Zemi v pevném bodě i u cestovatele na lodi stejný fyzikální čas, ale cestovatel udělá vůči Slunci o 1 otočku méně. Proto musíme tento 1 den, který ve skutečnosti uplynul přičíst, protože dny se počítají podle otáčení Země a ne podle „otáčení“ pohybující se lodi.

Pokud námořník pluje ze západu na východ a obepluje celou zeměkouli, tak jeho dny budou nepatrně kratší, protože pohyb Slunce na obloze urychluje a oproti pevné zemí vykoná za stejný fyzikální čas o 1 otočku vůči Slunci navíc. Tuto otočku, den, který ve skutečnosti neuplynul, musíme ze stejného důvodu jako v předchozím případě odečíst.

To ale platí jen pokud cestování trvá dlouho, déle než 24 hodin a cestovatel si měří dny sám, podle polohy Slunce na obloze. Cestování v minulosti většinou trvalo týdny, měsíce nebo i roky. Několikasekundové rozdíly v denním měření východů a západů Slunce se v průběhu výpravy nasčítaly na celý den. Tyto nepatrné téměř spojité denní odchylky času dnes reprezentují hodinové skoky (a přetáčení hodinek) při cestování po časových pásmech. V nějakém bodě se ty velké nebo malé skoky nakonec nahromadí a sečtou. Kde konkrétně ten bod bude je volitelné, ale někde to být musí.

Proto byla zavedena mezinárodní datová hranice na 180⁰ s jednoduchým pravidlem, že se po jejím přechodu bude 1 den (v závislosti na směru přechodu) přičítat nebo odečítat. Jenomže jedna věc je jednoduché pravidlo a druhá jeho pochopení.

Datová hranice jako důsledek a produkt
mapování času

Rotace pevného tělesa

Málokde jsou vidět důsledky mapování časových souřadnic na povrchu Země tak, jako u datové hranice. V reálném fyzikálním čase, který reprezentuje i naše chápání souvislostí a světa kolem nás platí, že pokud se nějaké těleso otáčí kolem své osy, tak právě proto, že všechny části tělesa jsou navzájem pevně svázané, otáčí se současně i každá část onoho tělesa. Na pevném tělese se nemůže něco točit a něco netočit. Buď se otáčí všechno, nebo se neotáčí nic. Otočení (rotace) Země kolem své osy o 360⁰ za 24 hodin proto nastane pro celé těleso vždy najednou a všude najednou také nastane po 24 hodinách „nový den tj. čas (24 hodin + t)“.

Cokoliv jiného je zcela „nelogické a nepřirozené“. Proto je z tohoto úhlu pohledu těžké pochopit, že někde vedle je „včera“, když je jasné, že vždy a všude kolem nás je „dnes.“ Včera je to, co už bylo. Bez mapování času by žádná datová hranice neexistovala. Nebo přesněji: datová hranice jako hranice dvou časů, do 24 hodin a nad 24 hodin (velkou jednotkou času je tu den), by za normálních okolností existovala jen v čase, ne jako oddělení dvou prostorů.

Mapování času a formalizmus vzniku nových dní na povrchu Země

Pokud namapujeme povrch Země podle toho, kdy kam zasvítí nějaké světýlko (např. světlo Slunce), a to bude v každém pásmu v jinou dobu (dle pásmových konstant), nastane i půlnoc v každém pásmu v jiném čase, a nový den pak začne v každém pásmu jindy. Pak se alespoň teoreticky může stát, že v kuchyni je dnes a vedle v ložnici je včera. Fakt, že se datová hranice vede většinou po moři na principu paradoxu nic nemění.

Příčinou časového paradoxu je jen formalizmus přiřazování časových souřadnic (synchronizovaných s cyklem Slunce) jednotlivým bodům na povrchu Země. Absurdnost některých situací nespočívá v nějaké nepochopitelné přírodní záhadě času, ale ve způsobu tvorby pásmový časů, tj. jednoho z časových systémů.

Nové dny na Zemi začínají postupně po pásmech. Jako první nastane půlnoc ve 12:00 GMT v pásmu +12. Potom následují každou hodinu pásma +11, +10, …, +1. Ve 24:00 GMT nastane půlnoc na Greenwichském nultém poledníku. Pak následují každou hodinu pásma -1, -2, …, -12. Tím je postupně ve všech pásmech zakončen 24hodinový cyklus. Poslední půlnoc bude v pásmu -12 ve 12:00 GMT. Ve stejnou dobu začne nový den v pásmu +12. Je to vidět na předchozím i následujícím obrázku (první obrázek „25 přímek“ se nachází v závěru 1. části studie). V pásmu +12 a -12 je na hodinkách „stejný čas“, ale v různých dnech, takže vzhledem k tomu, že den je také časovou jednotkou, ve skutečnosti čas v těchto pásmech není stejný, je posunutý o 24 hodin.

Mezi pásmem +12 a -12 vznikne skok o 24 hodinách. Vzhledem k tomu, že 24 hodin je 1 den, a dny v kalendáři označujeme číslem a měsícem, vlastně se na hranici změní datum a poledník mezi těmito pásmy tvoří datovou hranici. Podobně jako u časových pásem se i tady upřednostňují reálné geografické plochy s příslušným osídlením (ostrovy) před čistou matematikou souřadnic. Datová hranice proto není přesnou přímkou ze severního pólu na jižní, i když vede po moři.

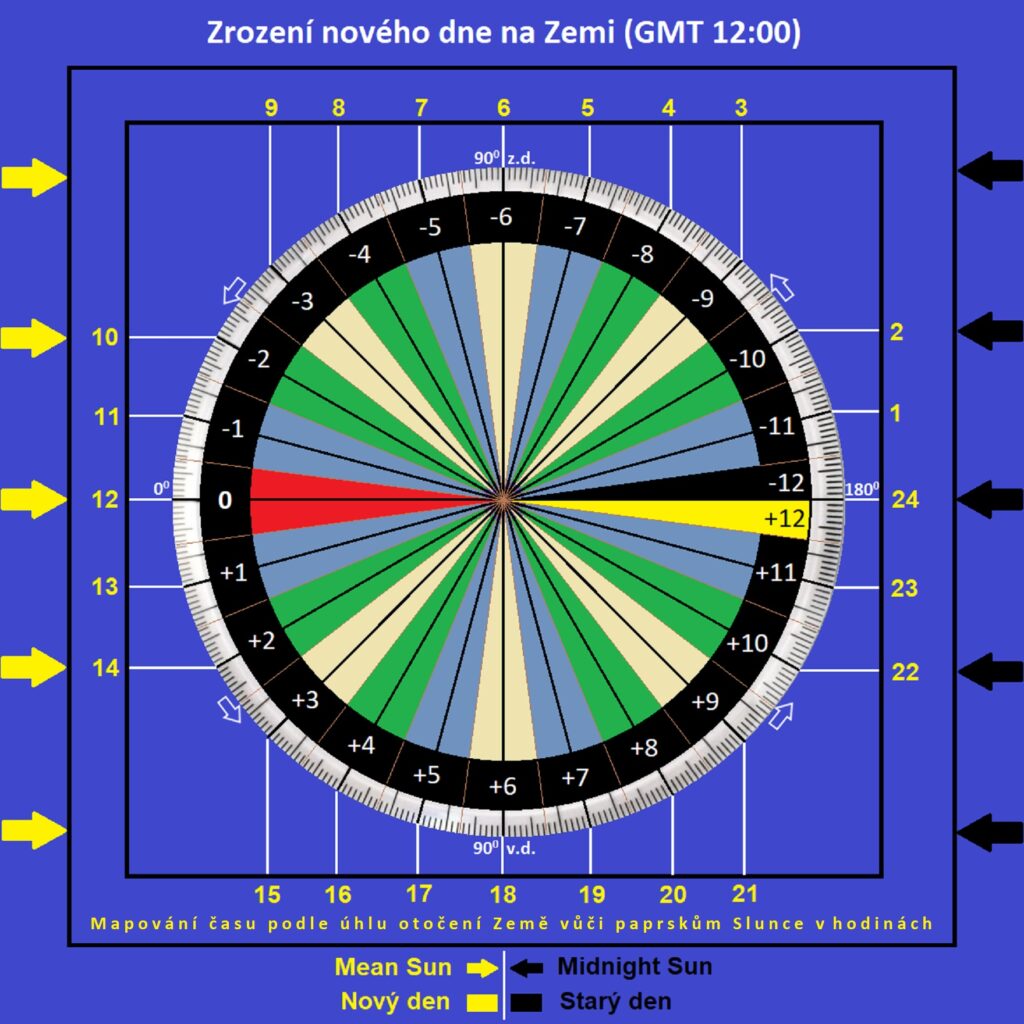
Obrázek – časová pásma a datová hranice

Pohled ze severního pólu

Na obrázku je vidět vznik nového dne na Zemi v pásmu +12. Nastává v čase 12:00 GMT. Nový den je zobrazen žlutou barvou stejně jako střední Slunce svítící zleva. Černou barvou jsou označena pásma, kde je ještě včera (o den méně). Černé „půlnoční“ Slunce (jako proti-poloha středního Slunce) je odpovědné za vznik času 24:00 v době jeho kulminace na příslušném centrálním poledníku. Datová hranice je čára mezi pásmem +12 a -12.

Vnější čísla reprezentují už probrané mapování času podle úhlu otočení Země vůči paprskům Slunce v hodinách. Jsou to stabilní, fixní polohy, místa na pevné myšlené kružnici. Zobrazují úhly, pod jakými svítí Slunce na tuto virtuální kružnici (0⁰, 45⁰, 90⁰,…). K těmto úhlům je možné přiřadit pevný čas v hodinách, minutách a sekundách. Je zobrazen žlutým písmem ve vnitřním čtverci obrázku.

Úhel (čas), kdy Slunce svítí na myšlenou úhlovou kružnici (povrch válce) kolmo je označen jako 12:00 a označujeme ho jako poledne. Pro opak 270⁰, „půlnoční Slunce“ je to 24:00 (půlnoc). Pro tečnu, tj. 0⁰ je to 6:00 a pro 270⁰ 18:00 (pro pravé Slunce to platí jen v době rovnodennosti). Další polohy následují vždy po 15⁰ a jsou označeny v hodinách, protože každou hodinu se Země otočí o 15⁰. Je to celá řada úhlů a příslušných časů. Na rozdíl od prvního obrázku spojitého mapování času zde už nejsou zakreslené „mezičasy“ jako 3:30 nebo 18:48, ale virtuální kružnice je i zde spojitá.

Odlišnost spočívá v tom, že na rozdíl od obrázku se spojitým mapováním (v 1. části studie), kde všechny body rovníku (a libovolné rovnoběžky) na točící se zeměkouli definovaly rotací svůj čas (2x spojitě), zde je aplikováno „kvantové mapování“. To reprezentují nespojité skoky z jednoho centrálního poledníku, definujícího svým otáčením čas, na druhý. „Právo na vlastní čas“ mají pouze centrální poledníky, ostatní body rovnoběžek (ohraničené pásmem) už ne a musí přebírat čas jim přiřazeného centrálního poledníku. Vlastní plynutí času v daném časovém pásmu určuje už spojitý pohyb centrálního poledníku pásma (rotace Země) podél virtuální kružnice.

Vnitřní čísla. Černá „kružnice“ (mezikruží) je pevně spojena se Zemí a zobrazuje úhly v intervalu 0 až ±180⁰. Jedná se o zeměpisné úhly na naší planetě (východní a západní zeměpisnou délku). Čísla označují zeměpisnou polohu, tj. pásma 0⁰, 15⁰, 30⁰, …, 180⁰. Opět ale nejsou vyznačena ve stupních, ale v hodinách a příslušný čas nám říká, o kolik je daná plocha povrchu Země při rotaci posunuta ve srovnání s polohou na Greenwich, kde definujeme nulu jako počátek. To je vždy co 15⁰, to další hodina (15⁰=1, 30⁰=2, 45⁰=3, …, 180⁰=12).

Poznámka k atomovému času

Současné taktování času atomovou sekundou na věci nic nemění. Systém pásmových časů zůstal a atomová sekunda se musela „naroubovat“ na původní sekundu tak, aby bylo vše ve shodě a časový systém nebyl narušen. Smyslem atomové sekundy je jen přesnější taktování. Odlišnosti v průběhu času jsou minimální a čas od času se vyrovnávají tzv. vloženou sekundou. Časový systém se ve své podstatě, tj. matematické konstrukci, nijak nezměnil. Atomová sekunda je srdcem „časového organizmu“ tvořeného pásmovým časem.

Důležité charakteristiky a vlastnosti
datové hranice

Kolik datových hranic vlastně existuje? Matematická nutnost existence druhé datové hranice

V běžně dostupných pramenech se popisuje vždy jen jedna hranice: Mezinárodní datová hranice – International Date Line (IDL) a uvádí se, že pokud by datová hranice neexistovala, tak by cestovatelům po objetí celé zeměkoule směrem na východ 1 den přebýval nebo směrem na západ naopak chyběl. Poprvé se tak stalo pravděpodobně u Magellanovy výpravy (1519 – 1522), protože předtím kolem Země nikdo necestoval, a tak bylo vytvořeno pravidlo, že po překročení mezinárodní datové hranice na 180⁰ ze západu na východ se 1 den odečítá a při cestě z východu na západ se naopak 1 den přičítá.

Historicky tedy potřeba datové hranice vznikla s cestováním a velkými výpravami kolem světa. V rámci jednoho pásma nevzniká problém, dny se střídají jeden po druhém a žádná záhada v tom není. Jak ale plyne z logiky věci i z topologie křivek, pokud na uzavřené kružnici označíme jeden bod a řekneme, že za ním bude platit nějaká vlastnost (nový den), přenese se ta vlastnost až na druhou stranu onoho bodu, a bude tam taky nový den. Už z obecné podstaty věci plyne, že na kružnici musí být ještě jedna hranice, kde se ta nová vlastnost ukončí, přestane platit.

Vznik druhé datové hranice a pohyb časových ploch s novým dnem

V momentě, kdy nastane v pásmu +12 půlnoc na 180⁰, začne nový den v celém pásmu najednou. Myšlenka pásmových časů znamená, že po průchodu centrálního poledníku daného pásma kulminačním bodem „půlnočního Slunce“ (proti-polohou středního Slunce), nastane půlnoc v celém pásmu, ne pouze na daném poledníku. Postupně, každou hodinu začne s půlnocí na následujícím centrálním poledníku nový den v dalším a dalším pásmu. A bude to pokaždé v celém pásmu najednou. Plocha, ohraničená dvěma poledníky, má dvě strany, proto k tradiční (v minulosti definované a popsané) mezinárodní datové hranici na 180⁰ (pevně svázané s povrchem Země) patří ještě jedna datová hranice (poledník), ohraničující plochu pásma (kde nastalo 24:00 a začal nový den) z druhé strany.

První datová hranice ohraničující časové pásmo (totožná s mezinárodní datovou hranicí), se vůči Zemi nepohybuje, ale vůči Slunci se rovnoměrně otáčí. Druhá datová hranice se pohybuje složitěji. Vůči Zemi je „periodicky“ hodinu pevná, nejdříve začíná v pásmu +12, na druhé straně plochy časového pásma, a každou hodinu, když nastane půlnoc v dalším pásmu skočí na kraj nového pásma s novým dnem, ale mezi skoky se (vůči Zemi) nepohybuje. Je to stejné jako kdyby se na nějaké ostře ohraničené ploše všude najednou rozsvítilo světlo, a pak v hodinových intervalech, opakovaně znovu a znovu na dalších plochách. V našem případě „půlnoční Slunce“ rozsvítí půlnoční tmu. Druhá datová hranice vůči Slunci zůstává trvale v pásmu „úhlu“ kolem 24 hod, tj. v oblasti „půlnočního Slunce“, pomalu se otáčí se Zemí a po hodině poskočí na kraj dalšího pásma.

Zajímavostí je, že k 24 hodinám je definováno 25, ne 24 různých časů. Z toho také plyne, že na Zemi nebude nikdy všude stejný den. Minimálně v jednom pásmu bude vždy buď „ještě včera“, nebo naopak „už zítra“ (z pohledu člověka na větším povrchu). Pravděpodobně to tak bylo zvoleno z důvodu symetrie, aby hranice procházela poledníkem 180⁰, jinak by datová hranice byla kvůli šířce pásma vůči nule na Greenwich asymetrická a číslování pásem taky (0, 1, 2, …, +12, -1, -2, …, -11).

Tento problém vzniká jen při skokovém mapování, při spojitém (v současnosti !nepoužívaném!) je šířka pásma nulová a v okamžiku kulminace „půlnočního Slunce“ nad první datovou hranicí je na celé planetě všude stejný den. Zároveň okamžik poté začíná na povrchu Země vznikat v prostoru mezi rotující první datovou hranicí (spojenou pevně se Zemí) a druhou datovou hranicí (spojenou pevně s „půlnočním Sluncem“) další den.

Poznámky ke grafu

Jedná se opět o pohled ze severního pólu. Na obrázku je vidět vznik nového dne na Zemi v prvních sedmi pásmech pro čas GMT 18:00. Nový den je zobrazen žlutou barvou stejně jako střední Slunce svítící zleva. Černou barvou jsou označena pásma, kde je ještě včera (o den méně). Pojem „půlnoční Slunce“ zde znamená jen proti-polohu středního Slunce (± 180⁰). Toto černé půlnoční Slunce je odpovědné za vznik času 24:00 v době jeho kulminace na příslušném centrálním poledníku. Podrobnější popis významu čísel je u předchozího obrázku. Druhou datovou hranicí je poledník na druhé straně žlutě vyznačené plochy.

První a druhá datová hranice, aktivní a pasivní překračování hranic

Mezinárodní datová hranice se dá překročit jen aktivně, protože je to čára pevně spojená s povrchem Země.

Druhou (vzhledem k povrchu Země pohyblivou) datovou hranici překročí každý člověk většinou pasivně, přirozeně a vědomě, bez překvapení. S příchodem nového dne nás hranice vlastně přeskočí (většinou jsme o půlnoci v posteli). Hranice s novým dnem přechází po povrchu Země s rotací Země a pohybem Slunce po obloze.

Překročení datové hranice je v tomto případě spojeno s přirozeně vnímaným plynutím času, s evidentním a zřejmým začátkem nového dne každé ráno a je proto pociťováno jako naprosto normální a běžné, nikdo půlnoc a nový den jako nějaké překračování datové hranice nevnímá, i když to tak je. Hlavním důvodem přirozeného vnímání této hranice je, že pokud jsme na jednom místě (například v posteli), tak nový den začíná v čase, a to je naprosto přirozené.

Spojení druhé datové a časové hranice s prostorem a její pohyb po povrchu Země člověk běžně nevnímá. Aktivní překračování této hranice z tohoto důvodu už tak samozřejmé a přirozené není. Právě naopak, takové aktivní změny mohou být pociťované jako velmi nepřirozené: například východ Slunce měnící se na západ Slunce při pozorování z velmi rychlého letadla letícího směrem na západ s cílem doběhnout půlnoc v jiném pásmu a dostat se do včerejška.

Druhá datová hranice se pohybuje velmi rychle. Z pohledu spojitého mapování na padesáté rovnoběžce o 18 km za minutu, z pohledu „skokového“ mapování skočí každou hodinu z pásma na pásmo o cca 1072 km. Aktivní překračování této hranice proto už není tak jednoduché jako u IDL, kde ji může překročit cokoliv, co umí plavat, i želva. Aktivní a pasivní překračování znamená velký rozdíl, dva různé světy. Překračovat druhou hranici aktivně oběma směry (a přes několik pásem) je v podstatě možné až v moderní době cestování velmi vysokými rychlostmi (letadlem, raketou). Na 50. rovnoběžce je potřebná rychlost řádově nad 1000 km/hod a na rovníku ještě mnohem víc.

Mnohonásobné překračování datových hranic, pravidlo na druhé datové hranici, schémata (1-1, 1+1)

Při aktivním překračování druhé pohyblivé datové hranice je vše opačně jako u pevné. Ze západu na východ se 1 den přičítá a z východu na západ odečítá. Přechodem obou hranic se dny vynulují, schéma (1-1). Nejlépe to je vidět na předchozím obrázku.

Při mnohonásobném obletu kolem Země proto k násobení dnů (za každý oblet) nedochází, protože překročením obou datových hranic se přidané a odebrané dny vynulují. Ze západu na východ jdeme na 180⁰ do včerejška, ale pak na druhé pohyblivé datové hranici zpět do dneška (a obráceně).

Pasivní překračování druhé datové hranice (první musíme překročit vždy aktivně) znamená jen jednu možnost, že se nový den přičítá, protože Země se točí jen jedním směrem.

Pokud tedy obletíme zeměkouli rychleji než za 24 hodin (letadlem nebo raketou), nemusí se datum změnit vůbec, změní se jen čas o dobu obletu. Závisí to na výchozím pásmu a rychlosti obletu. Například se datum nezmění, když vyrazíme z pásma, kde v průběhu hodiny nedojde ke změně data (je tam méně než 23:00) a obletíme Zemi za hodinu. Pří přechodu dvou datových hranic se uplatní výše uvedené schéma (1-1).

Ve speciálních případech může dojít k současnému nebo téměř současnému přechodu obou datových hranic najednou:

Schéma (1-1)
Pokud fyzicky projdeme (proplujeme) 1. datovou hranicí ze západu na východ (-1) a zároveň pasivně „překročíme“ 2. datovou hranici, tj. zrovna nastane půlnoc a začne nový den (+1) , pak bude následovat po sobě 2x stejný den.

Schéma (1+1)
Pokud fyzicky projdeme (proplujeme) 1. datovou hranicí z východu na západ (+1) a zároveň pasivně „překročíme“ 2. datovou hranici, tj. zrovna nastane půlnoc a začne nový den (+1) , pak je potřebné přeskočit celý jeden den a posunout se o dva dny.

Při skutečném cestování (nejen po matematických kružnicích) nebudeme přepisovat datum v průběhu dne, ale počkáme do půlnoci a přepíšeme ho podle některého z výše uvedených schémat.

Schémata (1-1) a (1+1) „v akci“ jsou vidět na prvním obrázku v závěrečné části článku o letu letadla kolem Země za 24 hodin. Je to obrázek „poslední hodina starého dne na Zemi“, čas GMT 11:00. Na změně data v pásmech +12 a -12 v průběhu jedné hodiny lze ilustrovat, co se stane, když současně projdeme obě datové hranice, první i druhou (IDL v prvním případě jedním a ve druhém opačným směrem). Na východ půjdeme ze soboty do soboty a na západ z pátku přímo do neděle.

Mezinárodní datová hranice jako
problém

Sňatek s kostlivcem jako sňatek z rozumu. Nebo z nerozumu?

„Kostlivec u datové hranice“ je nepříjemný a dává zabrat logice i vnímání současnosti, ale momentálně se musí tolerovat. Nic jiného nám nezbývá. Nedá se vyhnat, musíme s ním žít. Teoreticky je to rána do hlavy. Je to stejné jako kdyby někdo vytvořil nějakou matematickou strukturu, třeba ekonomický výpočetní systém, který by fungoval ve většině situací normálně a bez rozporů, ale v jedné speciální situaci by vyžadoval, aby čtyři jablka a čtyři jablka nebylo osm, ale osmnáct jablek.

Například pouze na Silvestra by platilo, že kdybychom v jednom obchodě koupili 4 jablka a ve druhém obchodě taky 4 jablka, tak do nějakého účetního systému by se muselo zapsat (a zaplatit) 18 koupených jablek, aby někde jinde v součtu „něco jiného“ souhlasilo, třeba počet vydaných šroubováků. Ale platilo by to jen pro jablka. Čtyři šroubováky a čtyři šroubováky by už nebylo osmnáct šroubováku, ale jen osm. Divné, co? Tak to dopadne, když se čas promítá na plochu jako nějaký film v kině.

Představa bytu, postaveného přes datovou hranici, kde v ložnici je pondělí 8:00 a v kuchyni je sice taky 8:00, ale už úterý, tzn. o 24 hodin více, nám změní „Schmetterlinge im Bauch“ na „Netopýři im Bauch“, tj. dost nepříjemný, ale také lehtavý pocit. V minulosti se to vědcům a technikům podařilo zamést „pod koberec“, i když konkrétně v tomto případě to šlo rovnou do moře, protože datová hranice je vedena právě z těchto důvodů po moři.

Kostlivec je tedy většinou na dně oceánu, ale kdyby tam byla souvislá pevnina a osídlená města, jedno za druhým po celém obvodu Země, bylo by to ještě zajímavé… Taková „losovačka“ by neměla chybu. V úterý v budovách „Sazky“ v pásmu +12 vylosovaná čísla, by se dala o několik desítek nebo stovek metrů dál, v pásmu -12 ještě v pondělí, tj. o den dříve, na poště podat jako náhodný tiket a v „dalších dnech“ i s vyhraným balíkem peněz vyzvednout a utratit. Podobný paradox nastává i na hranicích mezi pásmy, ale už jen hodinový.

Jiným reálnějším a realizovatelným příkladem paradoxu jsou lety do včerejška. Vzhledem k tomu, že tam je moře, nedají se dělat přímo vycházky uvedené v předchozím odstavci, ale stačí sednout na letadlo nebo na loď a za chvilku je člověk v jiném předchozím dni. Evidentně „něco“ není v pořádku…

Slabé místo zvolené matematické konstrukce mapování času by bylo nejlépe vidět v situaci, kdyby se Země otáčela velmi pomalu, 1 otočka vůči Slunci, 1 „sluneční den“ by trval například 5 let, taková situace není z hlediska fyziky ničím vyloučena. Něco by pomalu po celá léta brzdilo otáčení Země kolem osy, až by naše planeta rotovala uvedenou rychlostí. Aby se do toho nemontoval ještě oběh kolem Slunce, tj. roční cyklus, ten ať trvá třeba 500 nebo 1000 let, Země by pak byla na úplně jiné oběžné dráze, ale o to zde nejde. Hlavním cílem je tu princip tvorby časových souřadnic na povrchu planety.

Z tradičních důvodů bychom si zachovali nejen tradiční párky nebo bábovku, ale také tradiční, tj. současné jednotky času. Potom by nastala naprosto neuvěřitelná situace, že „symbolickým přeběhnutím“ datové hranice, by se dalo „dostat“ například z roku 2021 přímo do roku 2016, a to už je jiná káva než nějaký trapný přechod do včerejška. To by byl stroj času… Bohužel to ve skutečnosti funguje jen formálně. Čas se oklamat nedá.

Zóny UTC +13 a UTC +14 jako důsledek aktivity kostlivce od datové hranice

Kostlivec od datové hranice v moderní době řádí stále víc. Nakonec se po víc než 100 letech ukázalo, že i tam v Tichém oceánu, kolem datové hranice, na „území nikoho“, kde měla být jen voda a hejna ryb a ptáků, žijí lidé, kteří potřebují v moderním světě normálně fungovat. To je příležitost pro kostlivce, aby se realizoval. Vznikly tam okamžitě dva samostatné problémy, které následně svým řešením udělaly z exaktního měření času a z celého navrženého časového systému docela slušnou „bramboračku“ a rozbouraly už předtím velmi křehký a nedokonalý „systém a řád“.

První problém – využití letního času kolem datové hranice

I v pásmu UTC +12 potřebují státy a vybraná území někdy letní čas. Hodina navíc jako posunuté pásmo by normálně znamenala UTC -11, ale zde za hranicí je to sice o hodinu víc, ale předchozí den. Proto se definuje UTC +13 jako systémově neexistující časová zóna, ale přesto jednoduché a funkční řešení. UTC +13 používali v minulosti jako letní čas například obyvatelé ve východních částech Ruska ke svému standardnímu pásmovému času UTC +12.

Na jižní polokouli, na Novém Zélandu v pásmu +12 mají letní čas v době naši zimy (od září do dubna), takže do nového roku přechází v letním čase a nový den tam potom nastane ve fiktivním pásmu UTC +13, o hodinu dřív než normálně, tj. v čase GMT 11:00 (SEČ 12:00) místo pro GMT 12:00. Podobné je to i pro některé další ostrovní státy jako Samoa, Tonga, Tokelau s celoročním UTC +13.

Toto řešení lze považovat ještě za formální a není vyloženě antisystémové, na rozdíl od druhého.

Druhý problém – datová hranice a kalendářní časový skok v oblasti ostrovů kolem 180⁰ zeměpisné délky

Kiribati

Kiribati je rovníkový stát v Tichém oceánu, který se rozprostírá přes několik časových pásem. Ostrovy leží západně i východně kolem pôvodní datové hranice na 180⁰. Patří tam několik souostroví: Gilbertovy ostrovy (matematické pásmo +12), Phoenix ostrovy (matematická pásma -12 a -11), Liniové ostrovy (matematická pásma  -11 a -10). Celková délka ostrovů je až 4 000 km (pro srovnání Praha – Košice je vzdušnou čarou jen cca 520 km).

Každý začátek nového dne v průběhu roku v rámci matematické konstrukce časového systému nastává v pásmech -10, -11 a -12 až na závěr 24hodinového cyklu vzniku nového dne v jednotlivých časových pásmech povrchu Země. Silvestr a prvý nový den v novém roce by tam tedy ve skutečnosti dle řádného systémového mapování měl nastat až úplně na závěr dne silvestrovských oslav v čase GMT 10:00 (v pásmu -10), GMT 11:00 (v pásmu -11) a GMT 12:00 (v pásmu -12), ale (a to je důležité) až 1. ledna, ne 31.prosince. Jenomže stát Kiribati v roce 1994 provedl změnu svých východních zón -12, -11 a -10 na UTC +12, UTC +13 a UTC +14, aby země nebyla rozdělena datovou hranicí. Ta se touto operací prakticky posunula ze 180⁰ až do pásma -10, tj. o 30⁰ na východ na 150⁰ z.d.

Zprávy o těchto ostrovech a pásmech se proto objevují velmi často právě kolem Silvestra, protože v těchto zónách teď „oficiálně“ slaví konec roku dříve než v pásmu +12. Půlnoc se tu slaví už 31.12. o 1 a 2 hodiny dřív než pro řádný „systémový nový den“ v čase GMT 12:00. Konkrétně to vychází na GMT 10:00 a GMT 11:00. Vypadá to možná zajímavě, ale je to jen administrativní a nesystémová úprava.

Faktem ale je, že pro obyvatele dané krajiny bylo těžké udržovat kontakty a obchodní spojení s takovou systémovou zlomyslností jako je posun data v rámci jednoho státu. Mohou vznikat různé absurdní situace jako například to, že pokud jsou území posunuta o 1 den, úřední komunikace je možná jen 4 dny v týdnu, protože vždy 1 pracovní den v týdnu bude mít někdo víkend.

Posun datové hranice

Nová pásma narušují původní systém, kdy se nový den rodí vždy v pásmu +12. Do pásma +12  patří například Nový Zéland, kde by Nový rok měl správně začít jako první. Po něm následují postupně pásma +11, +10, …, 0, -1, -2, …, -11, -12. Jako poslední přichází nový den do pásma -12. Tam se celý cyklus o půlnoci následujícího dne uzavírá.

Fakt, že Gilbertovy ostrovy leží v pásmu +12 a ostatní ostrovy v pásmech -12, -11, -10 se dá řešit i jinak a logicky, že se datová hranice malinko posune na západ, aby pásmo -12 ostrovy obešlo a obyvatele nerozdělil datum. Pak mají v celém státu společný den. Na příkladu EU a jiných velkých států se ukazuje, že pásma je možné dokonce i sjednotit na společný čas (například -11 a -10). V každém případě by tam ale půlnoc měla nastat až na konci celého silvestrovského „dne oslav“, tj. druhý den dopoledne. Pro obyvatele ale bylo zřejmě důležitější se časově napojit na západní území jako je Nový Zéland (UTC +12) nebo sousední Marshallovy ostrovy (UTC +12) než na ty východní.

Uvedenou technickou úpravou se datová hranice v dané oblasti neposunula (o 30 min a 800 km) na západ kolem Gilbertových ostrovů, ale opačně (o dvě hodiny a víc než 3000 km na východ) až do pásma -10. V rámci turistického marketingu je pak možné po celý silvestrovský den hlásit v TV a psát v novinách, že jako první oslavili Silvestra obyvatelé ostrovů Kiribati. Ve skutečnosti se jen dohodli, že Silvestra budou slavit o den dříve než by měli. Zóny +13 a +14 vznikly z původního UTC -11 (předefinováním na UTC +13) a z UTC -10 (předefinováním na UTC +14). Další pásmo UTC -12 se tím automaticky proměnilo na UTC +12.

Nesystémové řešení

Antisystémové číslování pokračující za pásmem +12 znamená, že se obsadila část pásma -12 (nově +12), část pásma -11 (nově +13) a část pásma -10 (nově +14), ale zároveň původní pásma zůstala, ta nikdo nezrušil. A protože se ani nedají pořádně zakreslit dvě pásma přes sebe, je do těchto původních pásem (-10 a -11) pouze zaříznutý jakýsi „region – ostrůvek“ s UTC +13 a UTC +14.

Lidsky je to pochopitelné, ale technicky se jedná o docela slušný nesmysl. Při mapování pásem musí být rozsah mapovaného času 1 otočka – 1 rotace Země, tj. 24 hodin, rozhodně ne 26 a více hodin. Něco jiného je v rámci letního času přidat v pásmu +12 hodinu s vědomím, že jde pořád (reálně a zeměpisně) o pásmo +12 a něco jiného je kreslit jedno pásmo přes druhé a dělat z mapy bramboračku. Plochy času mají svá pravidla a ta jsou zde porušena.

Na Kiribati mají tedy půlnoc jako první jen proto, že každou půlnoc slaví o den dříve než jim to přísluší. Tady se kostlivec na datové hranici opravdu vyřádil. Zóny jen duplikují jiné už existující časové zóny. Východní oblast Kiribati se nachází ve stejném pásmu jako Havaj nebo Francouzská Polynésie (pásmo -10) a tam je o 11 hodin méně (ne více) než u nás (v pásmu +1) a nový den s půlnocí tam nastává řádně, tj. v závěru celého 24hodinového cyklu začínajícího nového dne na Zemi.

Reálně tedy v současnosti na ostrovech Kiribati fungují tato časová pásma (UTC +12, +13, +14): Gilbertovy ostrovy (UTC +12), Phoenix Islands (UTC +13), Line Islands (UTC+14). Jako první proto mají silvestrovskou půlnoc na Liniových ostrovech (atol Kiritimati – Vánoční ostrov) pro GMT 10:00, pak na Novém Zélandu (díky letnímu času) a Phoenix Islands pro GMT 11:00, pak Gilbertovy ostrovy pro GMT 12:00 atd.

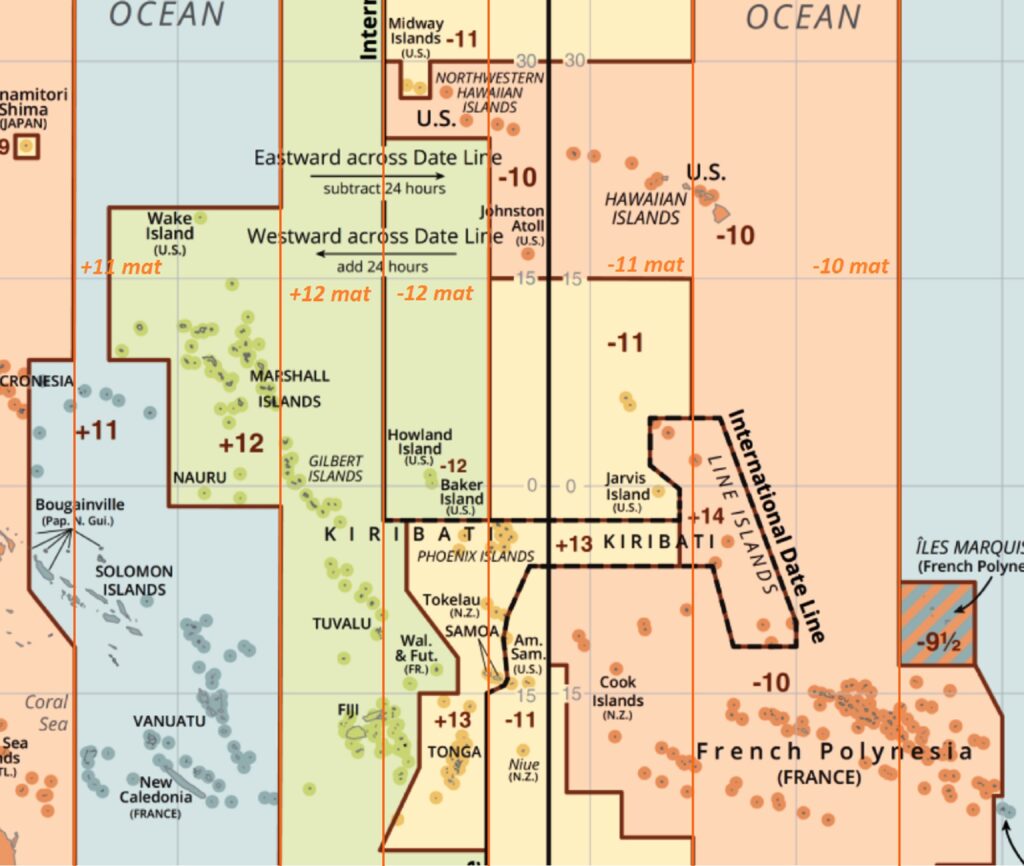
Obrázek je výřezem z mapy. Pro názornost jsou dokreslena ideální matematická pásma. Antisystémové překreslování datové hranice ilustruje chaos a problémy konstrukce časového systému.

Tři současné dny na Zemi aneb kostlivcovo „Schmetterlinge im Bauch“

Jako důsledek zavedení UTC +13 a UTC +14 (stačilo by pouze 1 pásmo UTC +13) mohou být na Zemi až tři různé datumy současně. Dva datumy současně přinesla přímo samotná matematická konstrukce systému mapování času. K 24 hodinám cyklu rotace Země je namapováno 25, ne 24 časových souřadnic. Z tohto důvodu v rámci skokového mapování není možné, aby na celé zeměkouli byl najednou všude jeden stejný den kvůli šířce pásem +12 a -12, kde skok o 24 hodin není jeden totožný bod (kde 24 hod = 0 hod), ale jsou to dva intervaly.

Při spojitém mapování může nastat všude jeden den současně, ale stejně jen na nekonečně krátký okamžik přechodu 1. datové hranice (IDL) druhou. Šířka pásma je nulová a počátek a konec cyklu (-12 a +12) potom splyne. Jinak bude někde vždy buď ještě včera, nebu už zítra. Pokud se k tomu přidají ještě dvě antisystémová pásma navíc (UTC +13 a UTC +14), tak pro:

GMT 10:00 bude v pásmech (-10 až +12) třeba sobota, v pásmech (-12, -11) pátek, v pásmu +13 bude také sobota, ale v pásmu +14 bude začínat neděle. Současně tedy bude pátek (-12, -11), sobota (-10 až +12, +13) i neděle (+14).

Za další hodinu bude pro:
GMT 11:00 v pásmech (-11 až +12) sobota, v pásmu -12 pátek, v pásmu +13 bude začínat neděle a v pásmu +14 neděle už bude, tj. celkem bude současně pátek (-12), sobota (-11 až +12) i neděle (+13, +14).

Za další hodinu bude pro:
GMT 12:00 v pásmu (-12 až +11) sobota , v pásmu +12 bude začínat neděle, a v pásmech (+13 a +14) bude neděle, tj. celkem bude současně sobota (-12 až +11) i neděle (+12, +13, +14). Dál už budou vznikat v dalších a dalších pásmech „normálně a systémově“ vždy jen dva dny současně až po další „periodicky stejný“ čas GMT 10:00 následujícího dne.

Jak je vidět z předchozího, zeměpisně (poledníkově) totožná pásma -10 (= +14) a stejně tak -11 (= +13) se liší konstantně v čase o jeden den.  

Pozn. 1: Pro tři současné dny by stačila i kombinace +12, -12 a +13, aby v čase GMT 11:00 byla jednu hodinu v pořadí sobota, pátek, neděle a po hodině nastala neděle, sobota, neděle.

Pozn. 2 (pro puristy): GMT je možné nahradit UTC.

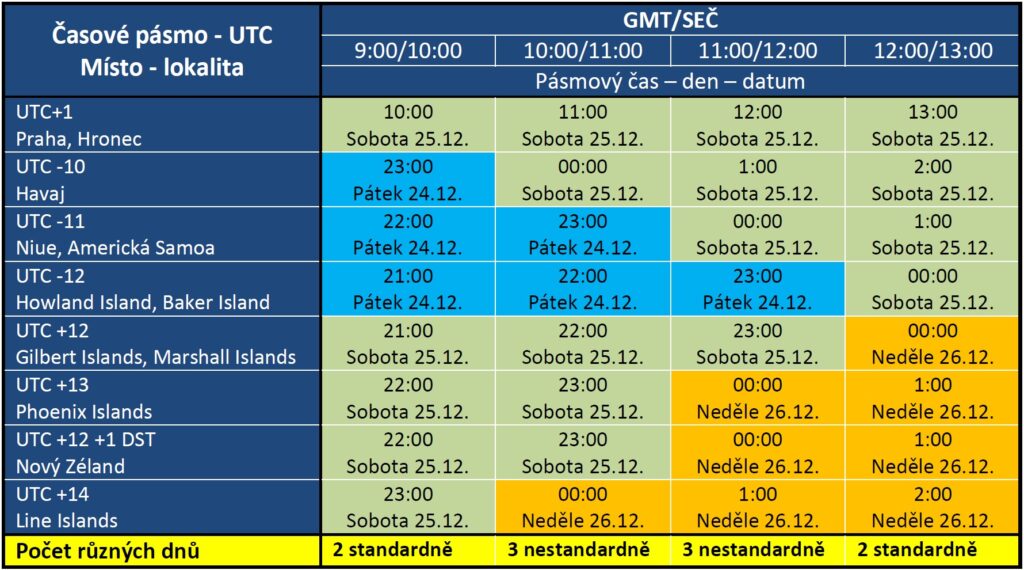
Kalkulátor času: https://time.is/cs/

Mezinárodní datová hranice jako
funkční řešení

Přechod datové hranice jako inverzní operace k mapování času

Na školení do mateřské školky

Je to jako hra ve školce, děti si nakreslí čtverce od 1 do 24, plus jeden s nulou, a v každém čtverci se bude měřit čas podle řádných hodin. Na začátku mají všechny děti stejný čas a stojí v prvním čtverci, kde je napsána nula. První dítě počká nějakou dobu (třeba 5 minut), a pak skočí do druhého čtverce a hodinky si tam posune přesně o 1 hodinu. Vždy se chvilku počká, je úplně jedno jak dlouho, čas běží všem stejně, a skáče se dál a dál, přitom se dodržuje pořadí čtverců. Z jedničky do dvojky, z dvojky do trojky atd. Po každém skoku se posouvají hodinky a vždy právě o 1 hodinu. Nakonec se obsadí všech 25 čtverců (0 – 24). Mezi prvním a posledním čtvercem vznikne rozdíl 24 hodin.

Pokud dítě zůstává v jednom čtverci, nevzniká žádný problém, ať už má hodiny posunuté jakkoliv, dokud neopustí čtverec, vše je O. K. Fyzikální čas může být měřen s libovolnou počáteční konstantou, která reprezentuje jen různé začátky měření času, a proto mohou být všechna měření v daném čtverci správná. Dají se měřit libovolné intervaly času s libovolnou přesností.

Potíže začnou, když budou skákat z jednoho čtverce do druhého, tam a zase zpět. Hodinky už nebudou synchronizované přesto, že na začátku měly všechny děti stejný čas. Při každém skoku je třeba hodinky posunout jedním nebo druhým směrem. Při každém pohybu zpět o stejnou hodnotu, o jakou se posunuly podle domluveného pravidla při pohybu směrem tam. Děti musí dělat inverzní operace, pokud se hodinky „posunuly“ o hodinu dopředu při skoku „tam“, posunou se o hodinu dozadu při skoku zpět. Pokud se posunuly o 5 hodin tam, posunou se o pět hodin zpět.

Čtverce můžeme uspořádat za sebou, jeden za druhým až do nekonečna. Po každém skoku z jednoho čtverce do vedlejšího bude vznikat „chyba“ z hlediska globálního a „ne-chyba“ z hlediska lokálního, viz poznámka o fyzikální konstantě. Lokálně, v rámci jednoho čtverce, tj. jednoho systému měření je vše v pořádku, globálně, v rámci všech čtverců, tj. všech soustav systémů měření, jsou systémy měření jako celek nesynchronizované. Chyba se bude podle počtu čtverců zvětšovat až do nekonečna. Může narůst i na stovky let a nikomu to v jeho čtverci (v jeho soustavě) nebude vadit.

Pokud ale seřadíme čtverce do kolečka a poslední čtverec se dotkne prvního, musíme se vrátit na začátek i se všemi vnesenými chybami a ne-chybami, provedeme synchronizaci a očistíme měření času od všech těch nasčítaných „nesmyslů“. Všechny ty skoky, to byla jenom hra, to nebyl skutečný čas. Skutečný čas mezi tím běžel na hodinkách všem stejně, tam jsou schované opravdové intervaly času, skutečný čas nedělá žádné skoky.

Takže se provede velký úklid a vše, co se v rámci skoků z jednoho čtverce do druhého nahromadilo, se zase jako nepotřebné harampádí vyhodí. Ať už to má kladné nebo záporné znaménko. Hodinky se totiž mohou v dané „hře“ posouvat nejen dopředu, ale i dozadu. A právě tohle je ten zázračný skok se změnou data (datumu) na datové hranici, je to jen velký servis. Přičtení nebo odečtení 24 hodin potom závisí na směru pohybu po nakreslených čtvercích.

Mapování času jako vědomé a organizované vnášení „chyby“ do časové mapy

Rozdíl mezi dětskou hrou a časovými pásmy je velmi malý. Když dítě skáče z jednoho čtverce do druhého, jedna hodina, o kterou si posune svoje hodinky je jenom hra s náhodně dohodnutou konstantou času. Děti se mohly domluvit, že si budou posouvat hodinky i o dvě hodiny (pokud by s tím souhlasila paní učitelka). Při konstrukci pásmového času hodnota posunu hodinek už není náhodná, ale odpovídá posunu Slunce na obloze. Promítání času na povrch Země je ale přesto jen konstrukce času vhodného k využití globálně stabilního rozvrhu hodin, tj. plánu činností v průběhu dne, protože časový systém a rozvrh hodin tvoří vždy tandem.

V minulosti totiž lidé ve své lokalitě i bez hodinek vnímali jako přirozené právě plynutí času podle Slunce od skorého rána, přes poledne a odpoledne až k večeru a následné noci. Na to si v průběhu staletí zvykli. Nikdo teď při společném globálním měření času nechce mít na hodinkách u oběda „půlnoc“, tj. 24:00. Přesto společným prvkem se skákací dětskou hrou je, že vlastní posouvání hodinek je i zde stále jen domluvenou „hrou“, žádný čas se při změně pásma ve skutečnosti neposouvá, čas běží na hodinkách stále stejně, je nezávislý a nějaká poloha Slunce na obloze ho absolutně nezajímá.

Čemu z pohledu mapování říkáme „oprava, korekce“ na pohyb Slunce je z pohledu fyzikálního času ve skutečnosti „chyba“ zanášená do řádného měření času. Při pohybu po uzavřené kružnici z východu na západ (Magellan) vneseme do měření času přechodem každého pásma chybu -1 hodina. Úplný oběh kolem Země potom vnese chybu – 24 hodin (nebo +1 a +24 hod při pohybu opačným směrem).

Rozdíl v chodu někdejších hodin u námořníků a dneškem je jen v tom, že jim se chyba sčítala po sekundách, pomalu a postupně. Tak malou odchylku na svých hodinách ani nezaregistrovali. Proto byli námořníci z Magellanovy výpravy plující kolem Země směrem na západ v šoku, když jim zmizel z lodních deníků celý den. My si při jízdě vlakem, autem nebo letadlem ze západu na východ posuneme hodinky po každém přechodu pásma najednou o celou hodinu přesto, že na hodinkách žádná další „přidružená“ hodina neuplynula. Čas, který při cestování běží na „stopkách v kufru“ žádnou další hodinu navíc nezaznamená.

Přechod mezinárodní datové hranice je proto operace (korekce) inverzní, která v rámci 24 hodinového cyklu vrací vše zpět. Jde o zpětnou synchronizaci časových souřadnic.

Který z pásmových časů je ten správný? Všechny nebo ani jeden?

Musíme se ještě jednou vrátit do mateřské školky. Co když se děti v rámci skákání z jednoho čtverce do druhého začnou hádat, kdo si má posunout hodinky. Vyřešit to může paní učitelka, která řekne, že správně jdou hodiny tomu dítěti, které do čtverce doskákalo jako první, v rámci obsazování čtverců hned na začátku hry. To první „okupační“ dítě v daném čtverci definuje systém měření, takže na tom kus pravdy je. Pravidla se mají dodržovat a některé děti to budou určitě respektovat, ale rebelové se budou hádat, že to jejich hodinky jdou správně a posunout čas si má to první dítě (a vůbec všichni okolo). Ani to nemusí být žádní myslitelé, jenom budou líní. Kdo má pravdu? Ve školce paní učitelka, ale jinak?

Když se podíváme na současný stav měření času na Zemi, tak k jednomu času namapujeme 25 (0, 1, 2, …, +12, -1, -2, …, -12) různých časů. Vzniká dost důležitá otázka přesahující rámec mateřské školky, který z těch časů je správný, a které jsou falešné.

Vzhledem k tomu, že čas můžeme měřit s libovolně zvoleným počátkem, z lokálního hlediska daného časového pásma je každý konkrétní čas vždy správný. Chybné jsou z pohledu globálního, protože není možné jednomu času přiřadit 25 různých časových souřadnic. Pokud si ale řekneme, že to je jen „hra“, že ty ostatní jsou jen mapované, virtuální, promítané na plochu, aby přinášely užitek jako slepice vajíčka, tak s tímto vědomím je můžeme akceptovat a tolerovat i všechny najednou. Ale podle toho se na ně musíme i dívat. a vědět, že přidružené časy nejsou skutečné.

Na grafu „25 přímek“ v 1. části studie byl fyzikální čas například zvolen tak, že byl ztotožněn s GMT, tj. s prostřední přímkou a mapované odchylky se pohybovaly od -12 do +12. To je ale jen volba a základní fyzikální čas může být zvolen libovolně, třeba ten v pásmu +12, nebo -12 (a jinak).

Časový paradox skoku do minulosti nebo do budoucnosti

Časový paradox z hlediska předchozích poznatků o mapování a následné inverzní operace na datové hranici

V jedné z předchozích podkapitol byl uveden příklad zvláštního „časového skoku“ o 5 let, přímo z roku 2021 až do roku 2016, který by bylo možné „udělat“ za jistých okolností pouhým přechodem datové hranice. O skutečném cestování v čase nemůže být bohužel ani řeč, ve skutečnosti matematická konstrukce tvorby časových souřadnic mapováním času podle pohybu Slunce na obloze v první fázi vytvoří chybu měření času 5 let (ve srovnání se skutečným fyzikálním časem), a na datové hranici ji potom skokově odstraní. Důležité je, že odstraňujeme chybu, kterou jsme sami způsobili.

Jak to vypadá konkrétně? Pro jednoduchost zachováme tradiční, tj. současné jednotky i „nakreslená“ časová pásma. Předpokládáme tedy, že den trvá 5 let a cestujeme na východ ze současného pásma -12. Potom si v následujícím pásmu -11 musíme hodinky s kalendářem přetočit ne o hodinu jako dnes, ale o 2,5 měsíce, aby se i v dalším časovém pásmu Slunce v kulminaci synchronizovalo s centrálním poledníkem jako teď (2,5×24 = 60 měsíců = 5 let). Kalendář jsou jen prodloužené hodiny, které reprezentují čas, proto musíme posunout i kalendář.

Se současnými jednotkami a hodinkami by to sice nebylo první další poledne, ale cca sedmdesáté páté (30 dní + 30 dní +15 dní), ale tato poledne by byla jen formální „nepravá“, bez Slunce nad hlavou. Po případné změně jednotek a s patřičně zpomalenými hodinkami by to ale mohlo být i první poledne s očekávaným časem 12:00.

V principu je úplně jedno, jak dlouho budeme kolem zeměkoule cestovat. Skutečná délka cesty se nepromítá do mapovaných virtuálních časů, ale do reálného času. Pokud nám to bude trvat 3 roky jako Magellanovi, cestou na východ uběhne na našich pásmových hodinách 8 let (3 roky + 24*2,5 měsíce), ale na stopkách jen 3 roky. Pokud jsme na výpravu vyrazili v roce 2013 přímo od datové hranice z dnešního pásma -12, tak po dlouhé 3 roky trvající námořní plavbě skončíme na opačné straně datové hranice v dnešním pásmu +12 s hodinkami a kalendářem, kde bude už rok 2021 (2013 + 3 roky_fyz + 5 let_map = 2021). Závěrečný skok do roku 2016 na datové hranici (2021 – 5) nás v rámci časového servisu jen přenese do reality a „skutečného času“, když se opraví do měření vnesené chyby měření.

V případě, že vyrazíme v roce 2013 od datové hranice opačně, na západ, hned na začátku si po přechodu datové hranice musíme přetočit hodinky o 5 let dopředu (nejdříve plujeme z dnešního pásma „-12“ do „+12“, po novém by to byla pásma „-2,5 roku“ a „+2,5 roku“) a dostaneme se skokem přímo do roku 2018. V rámce plavby uplynou na hodinkách 3 roky (tolik trvá plavba), ale zároveň si hodinky v každém pásmu musíme přetočit o 2,5 měsíce zpět.
Celkem to bude: 2013 + 5 let_map – (2,5 měsíce*24)_map + 3 roky_fyz = 2016.

Pokud bychom chtěli uvedený příklad s dnem trvajícím 5 let dotáhnout k dokonalosti, bylo by nutné překreslit pásma a změnit jednotky času. Samotná datová hranice by ale ve starých i v nových jednotkách (kde den trvá 5 let) zůstala na stejném místě. Hranice by oddělovala od sebe dvě časové plochy s rozdílem časů 5 let stejně, jako to dělá dnes s rozdílem časů 24 hodin. Rozdíl by spočíval v tom, že při použití tradičních, tj. současných jednotek času (z důvodu co nejjednodušší ilustrace časového skoku), by se dny měnily „tradičně, formálně“, tj. po 24 hodinách a tradiční roky po 365 tradičních dnech.

Velikost jednotek by na principu tohoto jevu nic nezměnila. Časový skok by zůstal ve stejné velikosti, ať už by byl uveden v libovolných jednotkách a s libovolným počtem časových pásem. Na tomto principu by se dalo „cestovat v čase“ přes libovolné intervaly času, klidně i o tisíce let. Velikost časového skoku jen zvýrazňuje absurdnost situace na datové hranici.

Datová hranice je podivná, ale funkční a nutná, zrušit se nedá

Přechodem datové hranice se čas a datumy vrací tam, kde patří, do normálních kolejí fyzikálního času. Podle směru cestování bude u časového paradoxu na datové hranici 5 let chybět nebo naopak přebývat. Může to vypadat divně (a divné to skutečně je), ale právě takto funguje mapování času podle Slunce, tj. hlavní systém měření času na Zemi.

Naštěstí v současnosti posun času není tak divoký, je to jen jeden jediný den trvající 24 hodin a z tohoto důvodu to nevzbuzuje žádné pozdvižení. Každý si řekne, že se tam „nějak“ posouvá datum, a je po problému. Navíc je tam moře, a tak nikdo nemá opravdu v ložnici pondělí a v kuchyni úterý. Pokud by to byl „den“, který by trval současných 5 let nebo by tam byla města plná lidí, asi by to vadilo víc a čas by se musel měřit jinak.

Skoky po pásmech a přes datovou hranici jsou tedy jasné, ale v případě námořníků v 16. století by si někdo mohl říci, že v době Magellanovy výpravy přece žádná časová pásma ještě nebyla (pásmový čas máme až od konce 19. století), tak proč potom tam vznikl problém?

Protože časová pásma a jim přiřazené časové skoky jsou schované v systému měření času podle Slunce, zda je zanášíme do měření nepozorovaně, spojitým mapováním po sekundách jako námořníci, nebo viditelnými hodinovými „skoky“ po časových pásmech, je ve výsledku jedno. Součtem je vždy chyba 24 hodin na 1 otočku Země. Tuto chybu datová hranice (při použití příslušného pravidla) odstraní.

Podstata časových paradoxů

Podstatou časových paradoxů při přechodu časových pásem, kde vznikají hodinové skoky (v kuchyni je o hodinu víc než v ložnici) je pohyb po časových plochách, podstatou paradoxů na datové hranici je periodicita a nahromadění malých „chybových“ skoků, tj. nutnost provést synchronizaci a vrátit se na začátek.

Časová pásma obsahují velmi podobný vnitřní problém jako matematické body v někdejším místním (bodovém) čase. V daném místě (bodě) na povrchu Země jsme sice mohli měřit čas, ale nesměli jsme se u toho pohybovat, jinak vznikal rozpor v současnosti dějů. To je zde podobné. Ve chvíli, kdy se začneme pohybovat mimo pásmo, nastane rozpor v současnosti dějů, jako u místních časů. Tři krávy na poledníku mají vždy stejný čas, ale tři krávy na rovnoběžce (zde v různých časových pásmech) už každá jiný. Časová pásma jsou jen roztažené (rozmazané) původní (matematické) body.

Pro samotnou časovou škálu „nakreslenou na povrch Země“ (tj. pro časová pásma) ani pro tělesa v rámci pásma nenastává promítnutím času na povrch Země žádný zvláštní problém. Ten nastane, až když se začneme pohybovat. Pokud se nepohybujeme mezi pásmy, je vše v pořádku. Ani byt na datové hranici, kde je v ložnici pondělí a v kuchyni úterý by nám nevadil, kdybychom trvale bydleli jen v jedné místnosti a nikdy se nepřesouvali do druhé. Vadit nám to začne, až když se začneme přesouvat z místnosti do místnosti.

Let kolem Země za 24 hodin

Pohyb těles mezi časovými pásmy a funkčnost datové hranice je možné ilustrovat na letu letadla kolem zeměkoule. Budeme cestovat rychlým letadlem, které obletí Zemi za 24 hodin.

Linka: Praha – datová hranice – Praha, podél rovnoběžky, směr východ

Představme si letadlo, které letí kolem padesáté rovnoběžky takovou rychlostí, že obletí zeměkouli za 24 hodin. Čas obletu je totožný s časem za jaký se Země otočí kolem své osy. Letadlo vyrazí z Prahy v sobotu ve 12:00, tj. přibližně z 15. poledníku (pásmo +1) a letí směrem na východ podél rovnoběžky. V kokpitu letadla sedí dva piloti, oba mají na rukách běžné náramkové hodinky. Každý je ale bude používat jinak.

První pilot bude měřit řádný fyzikální čas, a bude tedy používat hodinky jako stopky, nebude s nimi šibovat ani tam, ani zpět. Takové hodinky musí bezpodmínečně obsahovat kalendář, tj. musí násobky 24 hodin zobrazovat jako uběhlé dny. Hodinky nesmí největší časovou jednotku vynechávat. Vyloučit z měření času dny je stejné jako vážit kamiony a nezapisovat tuny.

Na začátku si oba piloti seřídí svůj čas se středoevropským časem (SEČ) hned na letišti. Druhý pilot bude mít hodinky seřízené stejně jako první, ale dál je bude používat už jako běžné pásmové hodiny, které se musí seřizovat s časem daného pásma, kde se bude letadlo nacházet.

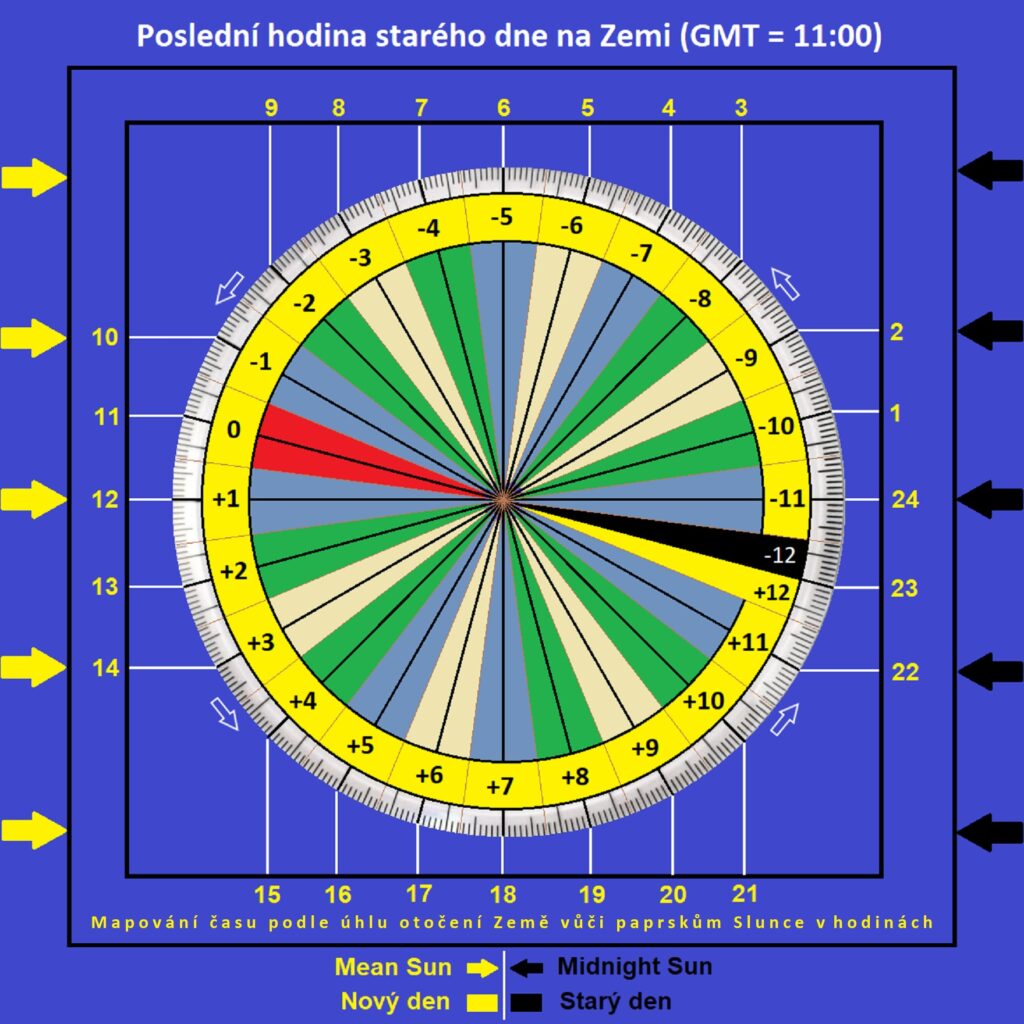
Start letadla a poslední hodina starého dne na Zemi

Graf znázorňuje start letadla v Praze ve 12:00 středoevropského času (GMT = 11:00). Obrázek ale také významně doplňuje první graf stejného typu ze začátku článku, kde je zrod nového dne na Zemi. Ten vzniká v pásmu +12 v čase GMT = 12:00. Situace zde je tedy těsně před. Za předchozích 23 hodin den postupně nastal ve všech pásmech, s výjimkou pásma -12. Za hodinu vznikne v pásmech +12 a -12 zvláštní situace. Pokud je v Praze a ve všech žlutých pásmech dnešní sobota, v pásmu -12 je ještě včerejší pátek. Za hodinu bude po půlnoci v pásmu -12 už také sobota a pásmo se tak připojí ke zbytku planety, kde sobota už je, ale zároveň v pásmu +12 nastane zítřejší neděle (v sobotu dnes a v neděli zítra). Z pohledu lidí v pásmu +12 bude ve stejném čase dnešní neděle a na zbytku planety bude ještě včerejší sobota (v neděli dnes a v sobotu včera). Je to děs jako u Felixe Holzmanna: viz Včera, dnes a zítra.

Praha – datová hranice, směr východ. Let kolem rovnoběžky může začít

Padesátá rovnoběžka má 25 728 km, pásmo je široké 1072 km. Pokud letadlo poletí rychlostí 1072 km/hod směrem na východ, přeletí pásmo za hodinu. Pásma +12 a -12 jsou poloviční, letadlo je přeletí za hodinu obě. 25 pásem (-12 až +12, plus 0) vytvoří 24 délek po 1072 km. Pokud by letadlo letělo kolem rovníku, princip je stejný, jen by muselo letět rychleji, protože rovník má 40 075 km.

Letadlo za 24 hodin obletí celou zeměkouli a skončí tam, kde vyletělo, na letišti v Praze. První pilot bude mít na hodinkách stejný čas jako při odletu, ale v kalendáři (a na dobrých hodinkách) bude mít zaznamenán o 1 den víc (12:00 + 24 hod = 12:00 + 1 den).

Úplně jiná situace nastane u druhého pilota, tam bude veselo. Tomu při přeletu jednoho pásma na hodinách sice taky uběhne jedna stejná hodina jako prvnímu, ale on chce mít hodinky seřízené s časem pásma, nad kterým přelétá (třeba tam chce něco sledovat a být synchronizován s „místním časem“), proto si každou hodinu musí posunout hodinky ještě o jednu další hodinu navíc. Poprvé si hodinky posune na hranici pásma +2 po půlhodině letu (z 12:30 na 13:30). Piloti budou ve stejné kabině, ale jejich časy se budou stále víc rozcházet a po přeletu jedenácti pásem to bude v pásmu +12 rozdíl až 11 hodin.

Pokud vyletěli z Prahy (pásmo +1) ve 12:00, po přeletu 11 pásem bude mít první pilot v pásmu +12 na datové hranici čas 23:00 a stále první den, tj. sobotu, ale druhý bude mít 10:00 a už neděli (12:00 + 11 hod _fyz + 11 hod_map = 10:00 +1 den). Druhý pilot naměří od pásma +1 po pásmo +12 (na svých podivných pásmových hodinách) o 11 hodin víc, tj. celkově 22 uběhlých hodin místo skutečných (fyzikálních) 11 (22 hod = 11 hod_fyz + 11 hod_map).

Piloti v tom mohou mít trochu guláš, kolik je vlastně hodin. První pilot měří „normální“ fyzikální čas a oprávněně se může domnívat, že on má „správný čas“. Jedinou výhodou druhého pilota je, že když on seskočí padákem kolem poledne podle svých hodin dolů, dostane v restauraci oběd (pokud najde nějakou otevřenou restauraci). Na rozdíl od prvního pilota, kterému hodiny sice „jdou dobře“, ale ve světě, kde všem okolo jdou hodinky „špatně“, mu to není na nic.

Přelet nad datovou hranicí

První pilot je na datové hranici v pohodě, ten má pořád svých 23:00 a stejný den, kdy vyletěli z Prahy (sobotu). Přechodem z pásma +12 do pásma -12 si ale druhý pilot musí posunout hodinky o 24 hodin zpět. Je proto ve stresu a má plné ruce práce, musí ručně přetočit hodinky s kalendářem o celý den. Chvilku to trvá, ale nakonec (v pásmu -12) bude mít na hodinkách stejných 10:00 (+ pár sekund nebo minut navíc, snad to nebude přetáčet hodinu), ale předchozí den, přetočením hodin „vejde“ znovu do soboty. Takže oba piloti už mají sobotu, ale první pilot má sobotu 23:00 a druhý sobotu 10:00.

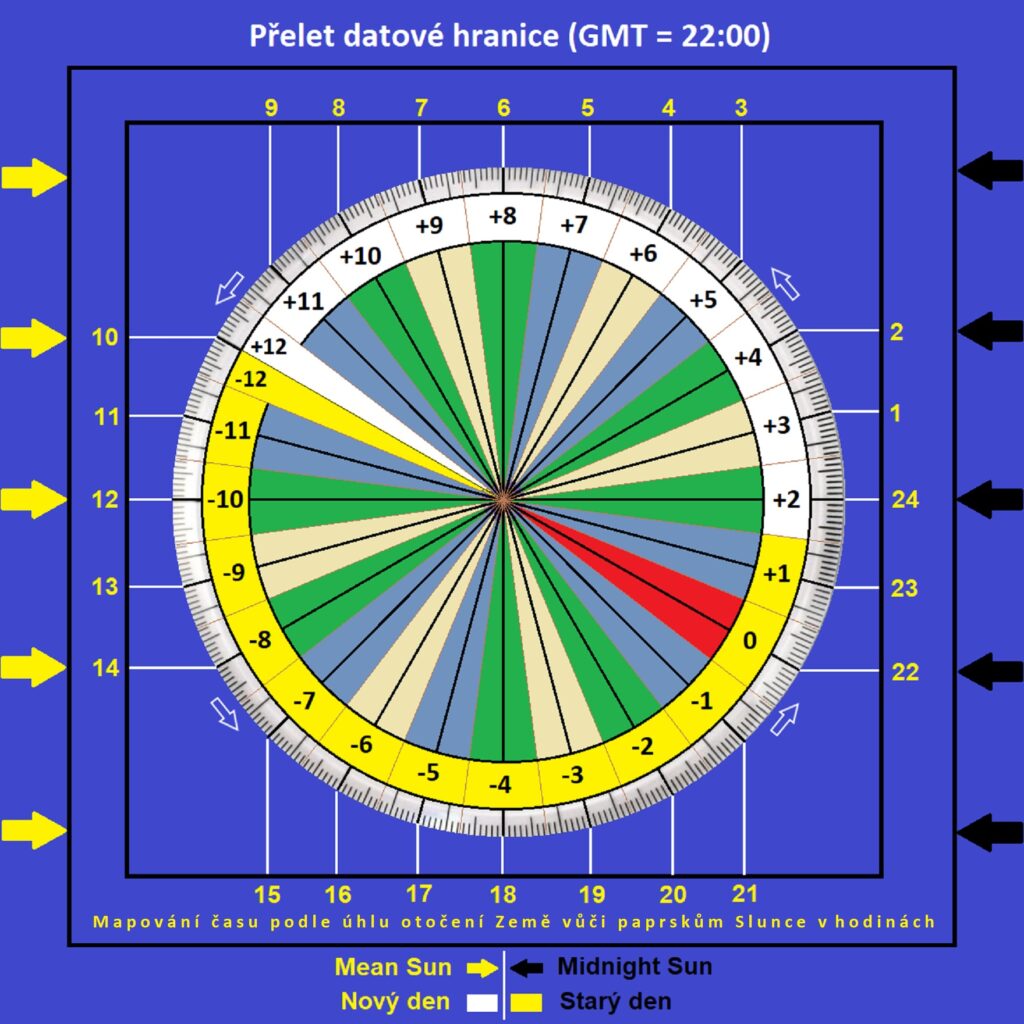
Datová hranice – Praha, podél rovnoběžky, směr východ

Prvnímu pilotovi půjde čas očekávaně, musí přeletět 13 pásem (vždy od jednoho středu pásma do druhého středu pásma), a to mu potrvá 13 hodin (23:00 + 13 hodin = 12:00 + 1 den). V Praze na letišti bude mít na hodinkách neděli 12:00. To nepřekvapí.

Druhý pilot na datové hranici (odečtením 24 hodin) především opravil do té doby vnesenou „chybu“ 11 hodin, kterou udělal tím, že neměřil skutečný čas, ale mapovaný. Zároveň však do řádného měření vnesl další „chybu“ -13 hodin (-24 = -11 – 13). Tím si vytvořil rezervu na sekání dalších a dalších chyb opačného plusového znaménka.

Mezi pásmem -12 a pásmem +1 musí přeletět spolu s prvním pilotem 13 pásem (-11 až -1, 0, +1). Tato předem vnesená chyba mu umožní, že v rámci přeletu uvedených dalších 13 pásem může „dělat další chyby“, tj. přičítat virtuální mapované časy a 13x vložit +1 hodinu přesto, že žádná neuplynula.

I tomuto pilotovi, který má na hodinkách sobotu 10:00, uběhne přeletem 13 pásem skutečný fyzikální čas 13 hodin. Na rozdíl od prvního si ale musí na hodinkách v každém pásmu přidávat ještě 1 pásmovou hodinu navíc. Celkem si tak přidá číselně stejných 13 hodin, jako jsou ty hodiny, které opravdu uběhnou v rámci letu kolem zeměkoule. Zaneřádí si tak řádné měření času chybou dalších 13 hodin, na kterou se ale na datové hranici připravil tím, že tam připočetl -13 neexistujících, tj. mapovaných hodin. Ve výsledku to bude 10:00 + 13 hod_fyz + 13 hod_map = 12:00 + 1 den. I on tedy bude mít na hodinkách neděli 12:00.

Platí sumární rovnice: 12:00 hod + 11 hod_fyz + 11 hod_map – 24 hod_map + 13 hod_fyz + 13 hod_map = 12:00 + 1 den_skutečný. Kruh se uzavřel a piloti vystoupí z letadla se synchronizovanými časy.

Tato rovnice jasně ukazuje funkci datové hranice jako křivky složené z bodů určených pro inverzní operaci k mapování, tj. z míst pro „časový servis“. Je to jako u auta, je třeba dofouknout kola, přeleštit zrcátko, doplnit olej…

Opačný směr: Praha – datová hranice – Praha, podél rovnoběžky, směr západ

U prvního pilota se nic nezmění, při letu nebude se svými hodinkami nic dělat. Při letu na západ bude hlavní rozdíl v tom, že druhý pilot si po jednu hodinu trvajícím přeletu každého pásma musí posunout hodinky pro změnu o jednu hodinu dozadu. Jemu se čas prakticky na 24 hodin zastaví. Ve 12:00 odletí z Prahy, ale už za půl hodiny tj. na hranici pásma Greenwich si musí ve 12:30 posunout hodinky o hodinu zpět a bude mít 11:30. Do dalšího posunu sice hodinky půjdou vždy normálně dál (11:30 – 12:30), ale každou hodinu až do pásma -12 si je bude posouvat stále na 11:30. Při spojitém mapování by hodinky doslova „zamrzly“ na místě s časem 12:00 a z běžných hodinek by druhý pilot musel vyjmout baterku, aby hodinky šly dobře.

Piloti budou mít skutečně trvale poledne, takže bude pohoda a až do Prahy mohou v klidu 24 hodin obědvat.

Přelet datové hranice

Prvnímu pilotovi ukážou hodinky po 13 hodinách letu v pásmu -12 na datové hranici čas 1:00 + 1 den (12:00 + 13 hod = 1:00 + 1 den).

Druhý pilot bude mít na datové hranicí po přeletu půl-pásma -12 přesně 12:00 a první den. Možná z toho bude i trochu nervózní, ale vzhledem k tomu, že může trvale obědvat, nakonec to psychicky určitě zvládne. Po přechodu datové hranice si posune hodinky o 24 hodin dopředu a nastaví si tam neděli 12:00.

Od datové hranice do Prahy

První pilot bude mít v Praze po dalších 11 hodinách letu (a přeletu 11 pásem) neděli 12:00 (1:00 + 1 den + 11 hod = 12:00 + 1 den).

Druhý pilot si po půl hodině letu a přeletu pásma +12 (na hranici pásma +11) přetočí hodinky opět na 11:30. Pak bude po přeletu dalšího a dalšího pásma přetáčet hodinky vždy ve 12:30 na 11:30. V posledním „domovském pásmu +1“ bude mít po přeletu půlky pásma za 30 minut na letišti v Praze nakonec správných 12:00 + 1 den (ten, který přidal na datové hranici).

Rekapitulace

V případě spojitého mapování by hodinky druhého pilota po dobu letu stály trvale, na datové hranici by je pilot posunul o jeden den dopředu a v cíli by to byl nakonec „správný“ čas totožný s časem prvního pilota. Říká se, že i hodinky na věži, které stojí, ukazují 2x denně správný čas. Zde by „zamrzlé“ stojící hodinky ukazovaly správný čas trvale.

Při skokovém mapování, podobně jako u prvního letu, druhý pilot na datové hranici nejen opravil do té doby vnesenou chybu -13 hodin (první pilot měřící de facto fyzikální čas má v pásmu -12 na datové hranici neděli 1:00, tj. o 13 hodin víc), ale vložil si do hodinek předem další „chybu“ +11 hodin (24 = 13 + 11), která mu umožní, aby mezi pásmem +12 a +1 mohl 11x „chybně“ posunout hodinky o hodinu zpět (-11), a přesto měl na konci letu v Praze na letišti správný čas.

Celkem je to po celém letu (12:00 + 13 hod_fyz -13 hod_map + 1 den_map + 11 hod_fyz – 11 hod_map = 12:00 + 1 den_skutečný). Slovo chybně je tu v uvozovkách, protože druhý pilot si z hlediska pásmových časů hodinky posouvá správně, ale chybně z hlediska měření fyzikálního času.

A poučení? V letadle je nejlepší se na pásmový čas vykašlat. Počítat se s ním dá, ale je velmi snadné udělat chybu. Nejlepší je pásmový čas ignorovat a na letišti se někde na vrátnici zeptat, kolik je vlastně hodin. Je totiž úplně jedno, kolik je „doopravdy“ hodin, hodinky nám musí jít hlavně tak, jako jdou lidem kolem nás. Taxikář na letišti si kvůli nám hodinky přetáčet určitě nebude.

Tento pásmový galimatiáš je ve skutečnosti v letectví řešen zavedením jednotného času, kterému se říká „zulu time“ (UTC + 0). Jinak by pilot kromě přetáčení hodinek už nic jiného nestihnul, o komunikaci mezi letadly a následných haváriích ani nemluvě. Více o času „zulu time“ je v článku: „Administrace přirozeného slunečního času“ v části o letectví.

Kolikrát jsme obletěli Zemi, jednou nebo dvakrát?

Při pohledu na kruhové grafy vzniká zajímavá otázka a objevují se i drobné pochybnosti. Kolikrát jsme vlastně obletěli kolem Země? V prvním případě to vypadá, že 2x a ve druhém případě se zdá, že vůbec. Ale zadání znělo: obletět Zemi za 24 hodin buď směrem na západ, nebo směrem na východ. Kdepak se vloudila chybička?

Jedná se o různé vztažné soustavy. Z pohledu letadla na povrch Země jsme v prvním i druhém případě skutečně Zemi obletěli 1x za 24 hodin, při pohledu z vesmíru (na Zemi a Slunce) letadlo v prvním případě obletělo kolem středu Země (jako bodu v prostoru) 2x, protože Země se za 24 hodin sama otočila kolem své osy jednou a letadlo muselo kolem středu Země „rotovat“ 2x tak rychle, aby vůbec nad povrchem letělo, tj. muselo vykonat vůči Slunci otočky dvě. Jednu otočku udělal i ten, kdo vydržel 24 hodin ležet na gauči.

Ve druhém případě letu na západ při pohledu z vesmíru letadlo vlastně stojí mezi Sluncem a Zemí, a Země se pod ním jen otáčí, piloti mají trvale poledne, tak dlouho, než přistanou. Proto hodinky druhého pilota při spojitém mapování stojí úplně a pilot může z hodinek vyjmout baterky. Hodinky (i s pilotem a letadlem) totiž trvale „visí“ v prostoru mezi Sluncem a Zemí. Při skokovém (kvantovém) mapování čas na hodinkách také skáče a kombinuje spojitý fyzikální čas s virtuálním skokovým tak, jak to pravidla o pásmových časech přikazují.

Třikrát poledne (2x snídaně, 2x oběd a 2x večeře) u 1. letu versus permanentní poledne s obědem, ale bez snídaně a bez večeře u 2. letu

Let na východ

Pokud budou piloti chtít zachovat rituál snídaně, oběda a večeře podle Slunce, budou se muset řídit podle hodinek druhého pilota. Jeho pásmové hodinky jsou „navržené“ pro zachování stejného rozvrhu hodin v globálním světě a zohledňují polohu Slunce na obloze.

První poledne s obědem nastává hned při odletu. První večeři si piloti dají už po třech hodinách. Dle druhého pilota bude totiž 18:00 (12:00 + 3 hod_fyz + 3 hod_map = 18:00). První snídaně bude po devíti hodinách. Dle druhého pilota bude 6:00 (12:00 + 9 hod_fyz + 9 hod_map = 6:00 + 1 den).

Druhé poledne s obědem nastane po 12 hodinách. Dle druhého pilota bude 12:00 (12:00 + 12 hod_fyz + 12 hod_map = 12:00 + 1 den). Druhou večeři si dají po patnácti hodinách. Dle druhého pilota bude 18:00 (12:00 + 15 hod_fyz + 15 hod_map – 24 hod_map = 18:00). Druhá snídaně bude po dvacet jedna hodinách. Dle druhého pilota bude 6:00 (12:00 + 21 hod_fyz + 21 hod_map – 24 hod_map = 6:00 + 1 den).

Třetí poledne nastane po 24 hodinách v cíli na letišti v Praze. Dle druhého pilota bude 12:00 (12:00 + 24 hod_fyz + 24 hod_map – 24 hod_map = 12:00 + 1 den_skutečný).

Let na západ

Při letu na západ mají piloti 24 hodin permanentní poledne s obědem. Druhému pilotovi hodinky cyklují mezi 11:30 a 12:30, ale celý 24 hodinový let bude bez snídaně a bez večeře, člověk nemůže mít všechno.

Krátké zamyšlení na závěr

Kde vlastně vzniká nový den a nové datum? Je to na datové hranici?

Slovo „vzniká“ znamená, že se vytváří něco nové, není to jen obyčejná změna. Když rozbijeme krásnou vázu, dojde ke změně stavu, ale neřekneme, že váza vznikla, spíše zanikla. Když potom střepy slepíme, provedeme opět další změnu, ale je to jen oprava vázy, která vznikla někde úplně jinde.

Formální změna data na 1. datové hranici znamená jen odstranění chyby v měření, která vznikla důsledkem mapování. Viditelný a trvalý zlom v čase, spojený s konkrétním místem v prostoru, kde se mění dny v kalendáři vytváří dojem, že právě tam „vzniká“ nový den a nové datum, ale to je omyl. Jen se tam opravuje chyba, jako když se na autobusu mění kolo. Ta chyba tam vždy byla, je a vždy bude. „Kolo na autobusu“ se tam bude měnit navěky, při každé jízdě.

Nové datum vzniká na druhé datové hranici, protože právě ona je spojena se skutečným Sluncem (u civilního času měřeného od půlnoci s „půlnočním“ černým Sluncem) a rotuje po povrchu Země resp. povrch Země rotuje vzhledem ke spojnici středu Země a půlnočního Slunce. Všechny body povrchu Země musí projít touto hranicí, která přináší půlnoc a nový den. To platí i pro body na první datové hranici. I tam vznikne posun v obou datech (v pásmu +12 a -12) jen tehdy, když projdou druhou datovou hranicí. Samotný časový zlom zůstává navěky stejný. Ne první, ale druhá datová hranice reprezentuje plynutí času a vznik nového dne.

První a druhá datová hranice v současnosti

Současné měření času je už jiné jako v minulosti, dosáhla se jednak velmi vysoká přesnost jednotlivých měření času, ale pokročila i globální synchronizace všech měření a změnil se i přístup k informacím o měření času. Nikdo si už neměří čas podle východů a západů Slunce. Reálné přechody pásem se řeší velmi jednoduše na základě centrálně řízených synchronizovaných pásmových časů.

Čas i datum na daném místě zeměkoule zjistíme z rozhlasu, z televize, z mobilu nebo z počítače. Hodinky si seřizujeme podle centrálního času pásma, kde se právě nacházíme a nemusíme nad tím vůbec přemýšlet. První a druhá datová hranice přesto existují i nadále, a někdy mohou být při řešení zajímavých otázek velmi důležité.

Datová hranice jako důsledek mapování času je centrem zajímavých situací i bodem možných problémů. Pro pochopení celého systému tvorby mapovaných časových systémů je právě datová hranice jako důležitá součást skládačky naprosto klíčová a celý systém tvorby času uzavírá. Přesto v reálném životě člověk může prožít celý život a nemusí o ní vědět absolutně nic.

***************

Konec 2. části

***************

1. část Studie časových systémů
Mapování času
2. část Studie časových systémů
Datová hranice
3. část Studie časových systémů
Plochy času
4. část Studie časových systémů
Správný čas

***************

Autor: Miloš Antes