Tento článek bezprostředně navazuje na trilogii „Přirozený sluneční čas (PSČ)“ publikovanou v roce 2018. Nový text a obrázky doplňují a rozvíjí původní text, z tohoto důvodu se tu neopakují ani nevysvětlují věci už popsané v předchozích částech. V úvodu je definován rozdíl mezi PSČ definovaným symetricky a stejným časem definovaným asymetricky. Následuje aritmetika časových jednotek pro posun času o 73 a 90 minut, včetně konkrétních hodnot pro variabilní sekundu, minutu, hodinu a den. Obě varianty posunu času doplňují i vztahy pro přepočet mezi PSČ a SEČ. Článek končí problematikou přestupného roku a vyrovnávání času mezi UTC (Coordinated Universal Time) a UT1 (Universal Time) v souvislosti s využitím PSČ.
Symetrický přirozený sluneční čas (SPSČ)
V článku o přirozeném slunečním čase (PSČ) z roku 2018 (https://zimnialetnicas.cz/prirozeny-slunecni-cas-2-cast/) byl výpočet nastaven tak, aby obrat v délce sekundy byl symetrický z pohledu středoevropského času (SEČ). Obrat nastal 182,5-tý den ve 12:00 SEČ (182,5-tý den ve 13:13 podle PSČ). To mělo za následek, že počet jarních a podzimních sekund nebyl stejný a důsledkem toho ani jejich „prodloužení“ nebo „zkrácení“ vůči „běžné“ sekundě nebylo stejné, bylo asymetrické.
Pro úvahy v článku to nepřinášelo žádný problém, přesto byla „ve vzduchu“ otázka, zda by nebylo lepší nastavit symetrii tak, aby počet jarních a podzimních sekund byl stejný a odchylka jarní nebo podzimní sekundy od „běžné“ sekundy byla pro obě sekundy (jarní a podzimní) stejná. Na následujícím obrázku je zobrazeno původní nastavení asymetrického PSČ z roku 2018.

Kdyby měl každý rok stejný počet dní, žádný zvláštní problém by nevznikal. Vadit by nám mohl jen oprávněný pocit, že počet jarních a podzimních sekund by měl být stejný (co je hezké bývá symetrické). Problém vznikne, když po čtyřech letech nastane tzv. přestupný rok s jedním dnem navíc a my zjišťujeme, že „nebude jednoduché“ rozdělit vložených 24 hodin (dle SEČ) na dvě části tak, aby se přírůstek času vyrovnal s úbytkem. Pokud jarní a podzimní sekundy nejsou symetrické, tak 12 j.h. + 12 p.h. (dle APSČ73) nedá 24 hodin dle SEČ. Vznikne časový rozdíl, který bude malý (pouze cca 0,0067 sek), ale nebude nulový.
Pokud chceme zahrnut do PSČ i přestupný rok, zvolíme přepočet tak, aby počet jarních a podzimních sekund byl stejný, pak bude délka jarních a podzimních sekund vůči běžné sekundě symetrická. Obrat musí nastat 182,5-tý den ve 12:00 PSČ (182,5-tý den v 10:47 dle SEČ). Takto definovaný čas je vhodnější pro praktické použití a umožňuje elegantní řešení problematiky přestupného roku. Graf průběhu východů a západů slunce pro SPSČ bude z důvodu malé odchylky stejný jako u APSČ.

Aritmetika sekund pro symetrický přirozený sluneční čas a posun o 73 minut
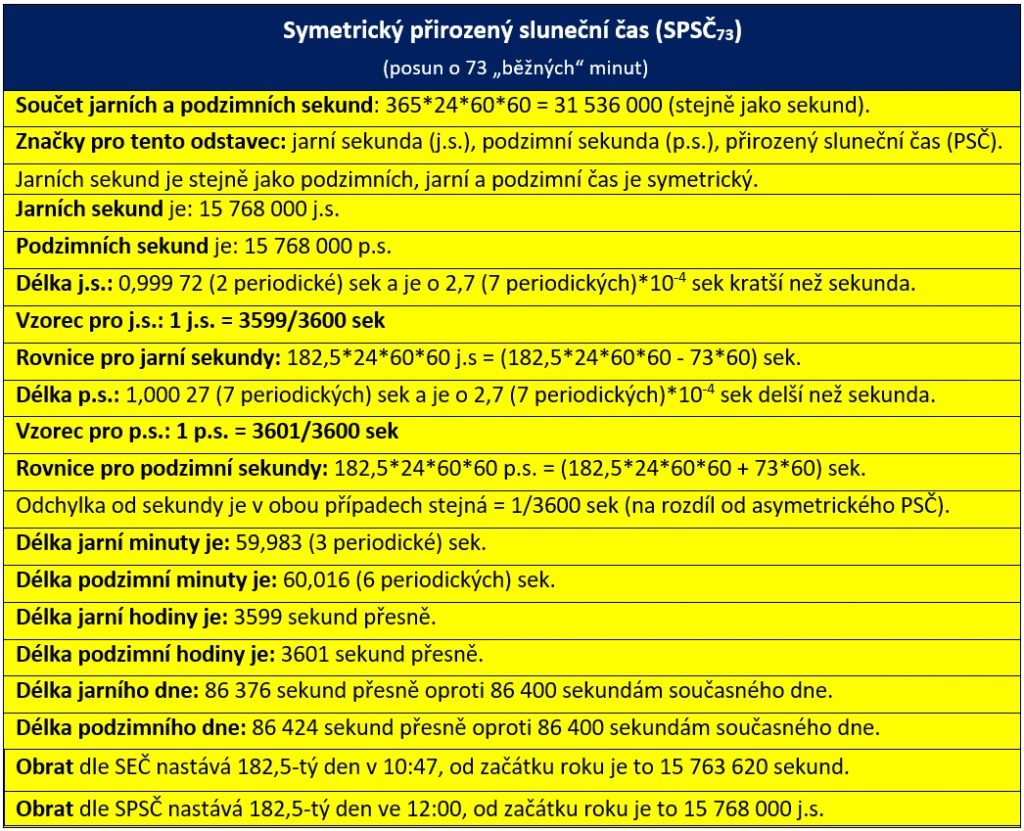
Přepočet mezi středoevropským časem (SEČ) a symetrickým přirozeným slunečním časem (SPSČ73) pro posun o 73 „běžných“ minut
s.s. – sluneční sekunda, společný název pro jarní nebo podzimní sekundu, stejný princip pro označování jednotek platí i pro minuty, hodiny a dny
Platí vztahy:
1 j.s. = 3599/3600 sek (1 sek = 3600/3599 j.s.)
1 p.s. = 3601/3600 sek (1 sek = 3600/3601 p.s.)
Obrat dle SEČ nastává 182,5-tý den v 10:47:00, od začátku roku je to 15 763 620 sekund.
Obrat dle SPSČ73 nastává 182,5-tý den ve 12:00:00, od začátku roku je to 15 768 000 j.s.
Přesný přepočet SEČ → SPSČ73
A – počet sekund od začátku roku do daného okamžiku, ale maximálně do bodu obratu [sek]
B – počet sekund od bodu obratu do daného okamžiku [sek]
C – celkový počet sekund od začátku roku do daného okamžiku [sek]
C = A + B
SPSČ73 [s.s.] = (A * 3600/3599 + B * 3600/3601)
Přesný přepočet SPSČ73 → SEČ
A´ – počet j.s. od začátku roku do daného okamžiku, ale maximálně do bodu obratu [j.s.]
B´ – počet p.s. od bodu obratu do daného okamžiku [p.s.]
C´ – celkový počet slunečních sekund od začátku roku do daného okamžiku [s.s.]
C´ = A´ + B´
SEČ [sek] = (A´ * 3599/3600 + B´ * 3601/3600)
Všechny běžně známé vztahy mezi sekundou, minutou, hodinou a dnem jsou zachovány i pro sluneční časové jednotky. Sluneční minuta má 60 slunečních sekund, sluneční hodina 60 slunečních minut a sluneční den má 24 slunečních hodin tj. 86 400 slunečních sekund.
Aritmetika sekund pro symetrický přirozený sluneční čas a posun o 90 minut
Jako příklad zde uvedeme ještě jednu velmi praktickou a zajímavou variantu s posunem času o 90 běžných minut vůči SEČ. Devadesát minut je možné rozdělit na 30 min a 60 min, pak je možné používat v zimě „pravý“ zimní čas s posunem východů slunce o 30 minut (slunce by v zimě vycházelo až o 30 minut dřív než při požívání SEČ). Zároveň by tento čas v létě spojitě přecházel na „letní čas“ s posunem o tradiční hodinu (slunce by v létě vycházelo až o hodinu později). Graf pro tuto variantu se nachází ve třetí části článku o PSČ z roku 2018 (https://zimnialetnicas.cz/prirozeny-slunecni-cas-3-cast/). Východy a západy slunce pro SPSČ jsou z důvodu velmi malé odchylky mezi symetrickými a asymetrickými veličinami prakticky stejné jako u APSČ.
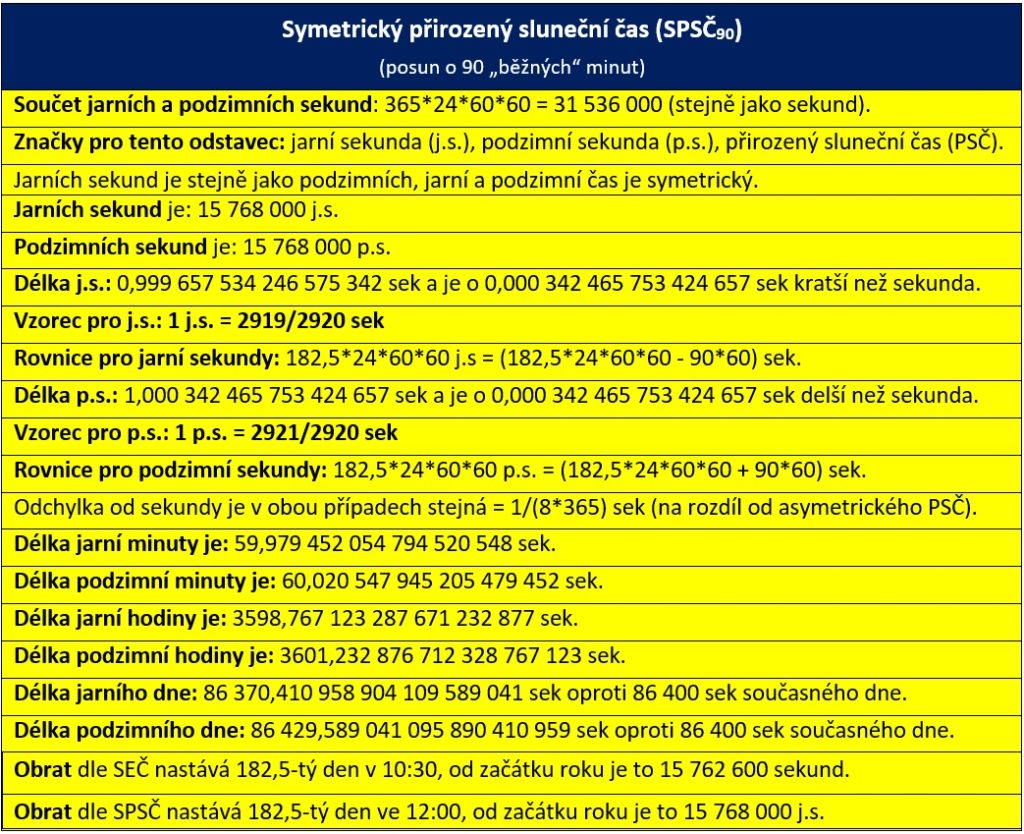
Přepočet mezi středoevropským časem (SEČ) a symetrickým přirozeným slunečním časem (SPSČ90) pro posun o 90 minut
s.s. – sluneční sekunda, společný název pro jarní nebo podzimní sekundu, stejný princip pro označování jednotek platí i pro minuty, hodiny a dny
Platí vztahy:
1 j.s. = 2919/2920 sek (1 sek = 2920/2919 j.s.)
1 p.s. = 2921/2920 sek (1 sek = 2920/2921 p.s.)
Obrat dle SEČ nastává 182,5-tý den v 10:30, od začátku roku je to 15 762 600 sekund.
Obrat dle PSČ nastává 182,5-tý den ve 12:00, od začátku roku je to 15 768 000 j.s.
Přesný přepočet SEČ → SPSČ90
A – počet sekund od začátku roku do daného okamžiku, ale maximálně do bodu obratu [sek]
B – počet sekund od bodu obratu do daného okamžiku [sek]
C – celkový počet sekund od začátku roku do daného okamžiku [sek]
C = A + B
SPSČ90 [s.s.] = (A * 2920/2919 + B * 2920/2921)
Přesný přepočet SPSČ90 → SEČ
A´ – počet j.s. od začátku roku do daného okamžiku, ale maximálně do bodu obratu [j.s.]
B´ – počet p.s. od bodu obratu do daného okamžiku [p.s.]
C´ – celkový počet slunečních sekund od začátku roku do daného okamžiku [s.s.]
C´ = A´ + B´
SEČ [sek] = (A´ * 2919/2920 + B´ * 2921/2920)
Také zde platí, že všechny běžně známé vztahy mezi sekundou, minutou, hodinou a dnem jsou zachovány i pro sluneční časové jednotky. Sluneční minuta má 60 slunečních sekund, sluneční hodina 60 slunečních minut a sluneční den má 24 slunečních hodin tj. 86 400 slunečních sekund.
Přestupný rok
Každý čtvrtý rok má 366 dní místo obvyklých 365 dní, a to v případě, že letopočet je dělitelný čtyřma (s výjimkami každých sto let). Den navíc se vkládá do měsíce únor jako 29. den v pořadí. V přestupném roku tedy únor nemá 28, ale 29 dní. Proč musíme vkládat každé čtyři roky 1 den? Protože oběh Země kolem Slunce netrvá přesně 365 dní, ale přibližně 365,25 dne. Bylo by docela překvapivé, kdyby oběh Země kolem Slunce trval přesně celočíselný násobek dnů tj. otočení Země kolem své osy. Tyto děje spolu totiž nesouvisí.
Při každém oběhu Země kolem Slunce (měřeném podle kalendářního roku o 365-ti dnech) Země na oběžné dráze zaostane o cca ¼ dne a tomu odpovídající vzdálenost. Roční období se v kalendáři posunou také na pozdější datum. Za 40 let se opozdí asi o 10 dní (9,7). Po staletích by to znamenalo, že léto by bylo v prosinci a zima v červnu (posun o půl roku by nastal za 753 let). Vkládání přestupného dne nařídil už Julius Caesar v roce 45 př.n.l., a zavedl tak na mnoho staletí juliánský kalendář.
Protože skutečná délka oběhu Země kolem Slunce je ještě trochu jiná, a to 365,24219 dne, roční období se i nadále posouvala, i když už pomaleji, cca 1 den za 128 let a pro změnu zas opačným směrem tj. na dřívější období. Proto zavedl papež Gregor (Řehoř) XIII. v roce 1582 ještě další korekci vztaženou na přesnější a realitě bližší číslo 365,2425. Nová korekce říká, že po každých 100 letech žádný přestupný rok nebude (0,24*100 = 24 dní, ne 25), ale po 400 letech ano (400*0,0025 = 1 den). Tento kalendář používáme dodnes jako tzv. gregoriánský kalendář. Ty „drobné“ mezi 365,2425 a 365,24219 se časem nasčítají a budou se muset jednoho dne opět řešit (cca za 3200 let takže to „nehoří“).
O této problematice existuje celá řada zajímavých a podrobných webů, například:
https://cs.wikipedia.org/wiki/Přestupný_rok
https://kalendar.beda.cz/prestupny-den
Přestupný rok a SPSČ
Jak řešit přestupný rok tj. vložený den o 24 hodinách složených z běžných sekund a minut v rámci nově navrženého systému s přirozeným slunečním časem?
Odpověď je jednoduchá až banální. Využijeme SPSČ a posuneme obrat o 12 j.h. (obrat nenastane 182,5-tý den ve 12:00, ale 183. den v 00:00 dle SPSČ). Oproti normálnímu roku necháme běžet ještě 12 hodin jarní čas a pak 12 hodin podzimní čas, vložíme tedy 24 hodin dle SEČ zároveň jako 24 slunečních hodin dle SPSČ.
Platí: 12 j.h. + 12 p.h. = 12*3600 j.s. + 12*3600 p.s. = 12*3600*((1 – Δt) + (1 + Δt)) sek = 24 hodin.
Δt – posun j.s. resp. p.s. oproti běžné sekundě (pro SPSČ obecně je interval pro obě sekundy stejný)
24 slunečních hodin je v tomto případě svojí délkou přesně rovno 24 hodinám dle SEČ.
Důležité je, že se v přestupném roce nemusí měnit délka slunečních sekund, vše zůstává platné. Rok o 366-ti dnech se prodlužuje o 24 slunečních (= 24 běžných) hodin. PSČ se během prvních 12-ti j.h. posune vůči SEČ v případě SPSČ73 o dalších 12 běžných vteřin a v průběhu následujících 12-ti p.h. se o stejných 12 běžných sekund vrátí zpět (pro SPSČ90 by to bylo o cca 14,79 sekundy tam a zase zpět). Zbytek roku před a po této „operaci“ je stejný jako v běžném roce s 365-ti dny.
Další posuny času a vyrovnávání rozdílů mezi UTC a UT1
Používané značky resp. zkratky v oblasti času
GMT – Greenwich Mean Time – Greenwichský střední čas, založen na rotaci Země
UT – Universal Time – Světový čas, založen na rotaci Země, obecnější pojem než GMT
UT1 – verze UT, zohledňuje pohyb rotační osy Země
UTC – Coordinated Universal Time – Koordinovaný světový čas, založen na atomových hodinách, nahradil GMT v roce 1972
UTC je koordinováno podle UT1 tak, aby rozdíl mezi UT1 a UTC byl menší než 1 sekunda
UTC+1, UTC+2 „zimní“ a letní čas v ČR
TAI – International Atomic Time (TAI), čas podle atomových hodin, od UTC se liší o vložené sekundy (UTC +37 sek = TAI ke dni 30. 3. 2020)
O významu značek a zkratek je víc zde.
Přestupná sekunda
V současné době je čas, který využívá periodický děj – otáčení Země kolem své osy (UT1), zpřesněn a zdokonalen jiným časem (TAI) založeným na periodickém procesu, který probíhá v atomu, a který je mnohem stabilnější než rotace Země. Tento čas je měřen podle tzv. atomových hodin a přesnost se tam blíží k dokonalosti. Koneckonců Země je jen „velká brambora“, která se otáčí kolem své osy a působí na ni další kosmické síly, které mají na otáčení a tím i přesnost periodického děje definujícího čas vliv. Nejvýznamnější je vliv Měsíce, který zpomaluje otáčení Země kolem své osy.
UTC je čas, jehož jednotky nezávisí na rotaci Země, ale jen na atomových hodinách. UTC je kombinace atomových hodin a korekce podle UT1, protože i UTC chceme svázat s rotací naší planety a nechceme, aby se tento čas od skutečného dne úplně „utrhl“. Aby se UTC a UT1 nerozcházely, vkládá se občas (např. v letech 2005, 2008, 2012, 2015, 2016) do UTC jedna sekunda, aby odchylka UTC od UT1, reprezentujícího skutečnou rotaci Země kolem své osy, byla menší než 1 sekunda.
Rotace se zpomaluje, proto přesných časových jednotek potřebných na synchronizaci s rotací bude třeba dlouhodobě stále víc (teď stačí cca 1 sekunda na několik let). Sekunda se vkládá tak, že v případě potřeby na Silvestra (nebo 30. června) po čase 23:59:59 následuje ještě 23:59:60 a až pak 00:00:00 jako začátek nového dne. UTC není GMT, UTC jsou vlastně tikající atomové hodiny, kde se jednou za pár let vloží přestupná sekunda.
Přestupná sekunda a SPSČ73
Úloha zní: vložit do SPSČ73 přestupnou sekundu z důvodu zpomalování rotace Země. Jak to udělat? Provedeme jednoduché posunutí „obratu“ o půl sluneční hodiny tj. v přestupném roce už na 23:30:00 místo 24:00:00 dle SPSČ a v běžném roce na 11:30 místo 12:00:00 dle SPSČ. Výsledkem bude posunutí o potřebnou sekundu.
Pokud posuneme uvedeným způsobem „obrat“, pro součet času za celý rok v běžných jednotkách bude platit následující:
(182,5 j.d. – 30 j.m.) + (182,5 p.d. + 30 p.m.) = 365 dní + (30 p.m. – 30 j.m.) = 365 dní + 30*60 (1 p.s. – 1 j.s.) = 365 dní + 30*60*((1 + Δt) – ( 1 – Δt)) sek = 365 dní + 60*60*Δt sek = 365 dní + 1 sek
Δt = 1/3600 sek
Touto velmi jednoduchou „operací“ je možné do daného kalendářního roku s přirozeným slunečním časem vložit 1 běžnou sekundu, aniž by se celkový počet slunečních sekund v daném roce změnil. Žádná přestupná sekunda, která by narušovala počet sekund v roce, se do PSČ vkládat nemusí.
Jaký nejmenší čas je možné vkládat do SPSČ73?
Princip přirozeného slunečního času umožňuje velmi elegantní posouvání času a vkládání libovolných časových úseků i mnohem kratších než je 1 sekunda. Nejmenší jednotkou, o kterou je možné posunout obrat je 1 j.s. (viz. poznámka) ve směru nebo proti směru hodinových ručiček (tj. dopředu nebo dozadu). Celkový počet slunečních sekund v průběhu roku musí být zachován a celočíselný (86 400 denně x 365 resp. 366 dní v roce). Kolik jarních sekund se přidá, tolik podzimních sekund se musí ubrat (a opačně). Posun obratu o 1 sekundu znamená buď o 1 jarní sekundu víc a o 1 podzimní sekundu míň nebo opačně.
Pozn.: Z pohledu času probíhajícího od začátku roku můžeme říci, že „obrat“ posuneme o 1 j.s. doprava nebo doleva. Z pohledu druhého „půl roku“ by se dalo říci, že „obrat“ posouváme naopak o 1 p.s. doleva nebo doprava. Vypadá to jako rozpor, ale není. Výsledek je samozřejmě v obou případech stejný, protože se jednotky navzájem vymění a celkový časový posun je jejich vzájemný rozdíl, který se touto úvahou nezmění. Je proto jedno jak to popíšeme.
Čas, který uběhne za rok při posunutí obratu o 1 „sekundu“ (o 1 čárku na hodinách):
- Obrat posuneme o 1 „sekundu“ zpět (proti směru hodinových ručiček) tj. rok bude mít o 1 j.s. méně a místo ní o 1 p.s. více (celkový počet slunečních sekund v roce bude stejný)
(182,5 j.d. – 1 j.s.) + (182,5 p.d. + 1 p.s.) = 365 dní +(1 p.s. – 1 j.s.) = 365 dní + ((1 + Δt) – (1 – Δt)) sek = 365 dní + 2*Δt sek = 365 dní + 2/3600 sek
V tomto případě se rok o (2/3600) sek prodlouží.
- Obrat posuneme o 1 „sekundu“ dopředu (ve směru hodinových ručiček) tj. rok bude mít o 1 j.s. více a 1 p.s. méně (celkový počet slunečních sekund v roce bude opět stejný)
(182,5 j.d. + 1 j.s.) + (182,5 p.d. – 1 p.s.) = 365 dní + (1 j.s. – 1 p.s.) = 365 dní + ((1 – Δt) – (1+Δt)) sek = 365 dní – 2*Δt sek = 365 dní – 2/3600 sek
V tomto případě se rok o (2/3600) sekundy zkrátí.
To samé jinak:
2 sekundy, na které by se změnila 1 j.s. + 1 p.s. nahradíme buď dvakrát j.s. nebo dvakrát p.s.
2 j.s. – 2 sek = (2*(1 – Δt) – 2) sek = -2*Δt sek (rok se o 2/3600 sekundy zkrátí)
2 p.s. – 2 sek = (2*(1 + Δt) – 2) sek = 2*Δt sek (rok se o 2/3600 sekundy prodlouží)
Nejmenší čas, který je možné vkládat do UTC je 1 běžná sekunda. Nejmenší čas, který je možné vkládat do SPSČ73 (nebo odečítat) je 5,5 (5 periodických)*10-4 sekundy.
Vkládání nebo vynechávání časových intervalů v rámci SPSČ obecně
Vzhledem k symetrii slunečních jednotek platí vždy, že součet „stejné“ jarní a podzimní jednotky času (sluneční sekundy, minuty, hodiny a dne) je 2x běžná jednotka času (sekunda, minuta, hodina a den). Naopak rozdíl „stejných“ jednotek bude vždy 2*Δt, kde Δt je odchylka dané konkrétní sluneční jednotky od běžné časové jednotky stejné „velikosti“, stejného „řádu“.
Například: 1 j.h. + 1 p.h. = ((1 – Δt) + (1 + Δt)) hod = 2 hodiny
1 j.h. – 1 p.h. = ((1 – Δt) – (1 + Δt)) hod = -2* Δt
Δt…odchylka sluneční jednotky od její běžné varianty, v tomto případě hodiny

Dva příklady pro SPSČ73: Posun obratu o 10 dní dříve by znamenal vložení 8 běžných minut (z tabulky 10*48/60) do kalendářního roku, aniž by se musel měnit počet sekund v daném roce. Posun obratu o 5 hodin později by znamenal vypuštění 10 běžných vteřin (z tabulky 5*2).
Přirozený sluneční čas umožňuje velmi dobrou koordinaci s robotickými časy UTC i UT1. Sluneční sekunda (jarní i podzimní) může být z hlediska délky jednotky času taktována i seřizována na základě atomových hodin a koordinace přirozeného času s UT1 tj. s rotací Země se může odehrávat v oblasti posunu „obratu“. Pokud bude zpomalování rotace Země pokračovat, vložených sekund bude třeba stále víc a budou se vkládat stále častěji. Právě zde je výhoda PSČ, který to může v rámci vhodně definovaného obratu elegantně zvládnout.
Odchylka mezi symetrickými a asymetrickými sekundami

Jak už bylo řečeno na začátku tohoto článku, trilogie „Přirozený sluneční čas“ pracovala s jednotkami nastavenými asymetricky. Tabulky a grafy uvedené na konci druhé a začátku třetí části původního článku z roku 2018 byly spočteny pro APSČ. Můžeme si položit otázku, jak se budou odlišovat „nové“ tabulky a „nové“ grafy východů a západů slunce pro symetrický PSČ od těch původních.
Pro posun o 73 minut je rozdíl mezi jarními sekundami -1/(3600*3601) sek. To je hodně malé číslo a znamená, že symetrická j.s. je o něco menší než asymetrická. Za 182,5 dne, tj. v době, kdy graf pro PSČ vrcholí (dosahuje maximální odchylky od běžného času), rozdíl mezi symetrickým a asymetrickým PSČ dosáhne hodnoty asi 1,2 sekundy. Vzhledem k tomu, že tabulky a grafy byly spočteny s přesností cca 1 minuty, platí jak pro symetrické, tak pro asymetrické hodnoty přirozeného slunečního času.
Pro posun o 90 minut je rozdíl mezi jarními sekundami -1/(2920*2921) a za 182,5 dne rozdíl dosáhne hodnoty cca 1,8 sekundy. Ani v tomto případě se tabulky ani grafy nezmění. Pro názorné zobrazení funkčnosti SPSČ proto není nutné vytvořit nové tabulky ani překreslovat grafy.
„Obrat“ pro SPSČ v tabulce východů a západů slunce se bude samozřejmě od „obratu“ pro APSČ už dříve popsaným způsobem lišit, a to pro obě verze (73 i 90 min), ale na grafech se posun obratu vzhledem k měřítku (osa x je v měsících) neprojeví.
Autor: Miloš Antes
