Plochy času

Plochy času jsou skutečné reálné plochy (povrchy), které obsahují souřadnice času promítané v daném okamžiku na povrch Země. Vznikají v časových systémech, které využívají polohu Slunce na obloze k vytváření sítě časových souřadnic přiřazených k souřadnicím povrchu. Plochy času je možné zkoumat z různých hledisek, kterým potom odpovídají různé typy grafů. Výsledkem odlišných pohledů je lepší pochopení fungování časových systémů. Grafy evoluce časových ploch umožňují jednoduché a názorné zobrazování pohybu těles po časových plochách s jasným odlišením reálných a virtuálních mapovaných časů. Tyto grafy mohou tvořit jednoduchý záznam nebo naopak plán poloh a příslušných časů při pohybu letadla, lodě nebo rakety.

Když dva dělají totéž, a není to totéž

U zdánlivě stejných věcí nemusí fungovat stejné vnitřní propojení, a proto ani výsledek nemusí být stejný. Kouzlo, které je u časových systémů dobře schováno spočívá v tom, že je lehké a lákavé zaměnit čas, který je v jedné situaci skutečný, s jiným, zdánlivě velmi podobným (skoro totožným), který už ale skutečný není, protože funguje v principiálně odlišné situaci a ve skutečnosti se netýká stejné věci.

Tou první situací je reálný fyzikální čas, kdy se Země za 1 hodinu opravdu otočí o 15⁰, to je děj, který probíhá ve skutečném čase. Pokud ale tento čas začneme systémem mapování času promítat na plochu (povrch Země) jako film, viz obrázky z 1. části studie (ať už je to spojité nebo skokové mapování), pak mezi body tohoto „plátna“ povrchu Země takto definovaný čas už neprobíhá. Tyto body mají stejný čas a děje s nimi spojené jsou současné.

Skákací hra, kde si děti hrají tak, že skáčou z jednoho čtverce do druhého (viz díl o Datové hranici) je zde jen trochu větší, je totiž nakreslena na povrch Země jako 24 resp. 25 „čtverců“ s namalovanými čísly, o kterých „předstíráme“, že jsou spojené s časem. Nejsou, sice nevznikly úplně náhodně jako nějaké sprejerské dílo, ale ani velmi seriózní a složité promítání polohy Slunce na obloze na plátno povrchu Země nic nemění na skutečnosti, že promítnuté „čtverce“ nejsou časem ani náhodou. Je to jen kresba, mapa času na povrchu Země.

Grafy časových ploch proto musí respektovat realitu a zobrazovat kvalitativní odlišnost jednotlivých časů. V grafické podobě musí být mapovaný virtuální čas jasně odlišen od fyzikálního tam, kde to je možné nebo nutné. Časy se liší i svým rozsahem. Rozpětí fyzikálního času je nula až nekonečno, rozpětí mapovaného času je nula až 24 hodin (alespoň za normálního stavu, pokud z toho někdo nezačne dělat bramboračku, viz článek o Datové hranici). Lety do včerejška proto možné jsou, ale lety do před-včerejška už ne, ani v reálném, ani ve virtuálním čase (antisystémová pásma UTC +13, +14 zde do úvahy nebereme).

Prvý a základní způsob zobrazení plochy času

Prvý způsob zobrazení byl popsán už ve Studii časových systémů 1 a následně několikrát využit ve Studii časových systémů 2. Plochy času jsou v nich zobrazené jako časy promítnuté na dvourozměrný kruhový obrázek nahrazující povrch zeměkoule. Jednotlivým plochám ohraničeným poledníky byly na principu skokového mapování přiřazené časové souřadnice vždy pro jeden konkrétní časový okamžik, který je definován hodnotou času měřeného jako GMT. Takto bylo na základě skokového mapování zobrazeno několik časových verzí jednotlivých ploch času pro GMT = 11:00, 12:00, 18:00 a 22:00 hod.

Zkratka GMT byla použita jako symbol způsobu promítání středního Slunce na povrch Země, pocházejícího z astronomických měření, ale v principu se může jednat i o symbolické abstraktní „atomové Slunce“ nahrazující střední Slunce (resp. „atomovou Zemi“ s dokonale vyhlazenou rotací) a taktující čas jako UTC, tj. na základě atomových hodin. Taktování času se se tím jemně upřesní, ale klíčový princip promítání času na plochu zůstane nezměněn.

Použitý graf umožňuje velmi názorné promítání času na povrch Země prostřednictvím virtuální kružnice spojené s ideálním „abstraktním Sluncem“, která v každém konkrétním časovém okamžiku definuje na povrchu Země časy UTC (GMT). Důsledkem je například to, že se datová hranice jako časová souřadnice oddělující dvě data (a dva časy) promítne z veličiny časové na veličinu spojenou s prostorem v podobě mezinárodní datové hranice.

Na rozdíl od normální (druhé) časové a datové hranice probíhající jen v čase, která odděluje číselným údajem 24 hodin časy 24 – ε a 24 + ε pro ε > 0, je na mezinárodní datové hranici trvalý časový zlom 24 hodin, který opravuje nahromaděnou chybu. Žádná kontinuita plynoucího času jako u běžných časových souřadnic, ale konstantní časová propast.

Nevýhodou tohoto způsobu zobrazení je, že se pro každý další čas GMT musí obrázek nakreslit znovu. Tato nepříjemnost se dá odstranit, pokud se obrázek namaluje na nějakou čtvrtku a kružnice se vystřihnou tak, aby umožňovaly otáčení. Nebo může změny konfigurace časů zajistit jednoduchý grafický program.

Evoluce plochy času a pohyb mezi časovými pásmy

Druhým typem zobrazení je graf „25 přímek“ zmíněný a popsaný už v 1. části studie časových systémů. Ten umožňuje zobrazit mnohem víc, než se na první pohled zdá. Úsečka vlevo (křivka 1) je jedním (kolmým) rozměrem časové plochy. Je to vlastně mapa (fotka) promítnutých časů kolem rovníku v daném časovém okamžiku (zde 12:00 GMT). Úsečka jako celek vznikla na základě spojitého mapování.

Body zobrazující celá čísla na ose y a z nich vycházející časové přímky reprezentují skoky „kvantového“ mapování (spektrum hodnot), které je provedené centrálními poledníky 0, 15, 30 …, stupňů. Úsečka vedle osy y reprezentuje časovou plochu (když už jsme čas promítli na povrch Země) a další plocha grafu nakreslená v rovině xy mezi horní a dolní přímkou (pásma +12 až -12) zobrazuje změnu, časový vývoj plochy času (zde zobrazené jen křivkou 1) včetně evoluce celého spektra časů, které vzniklo skokovým mapováním.

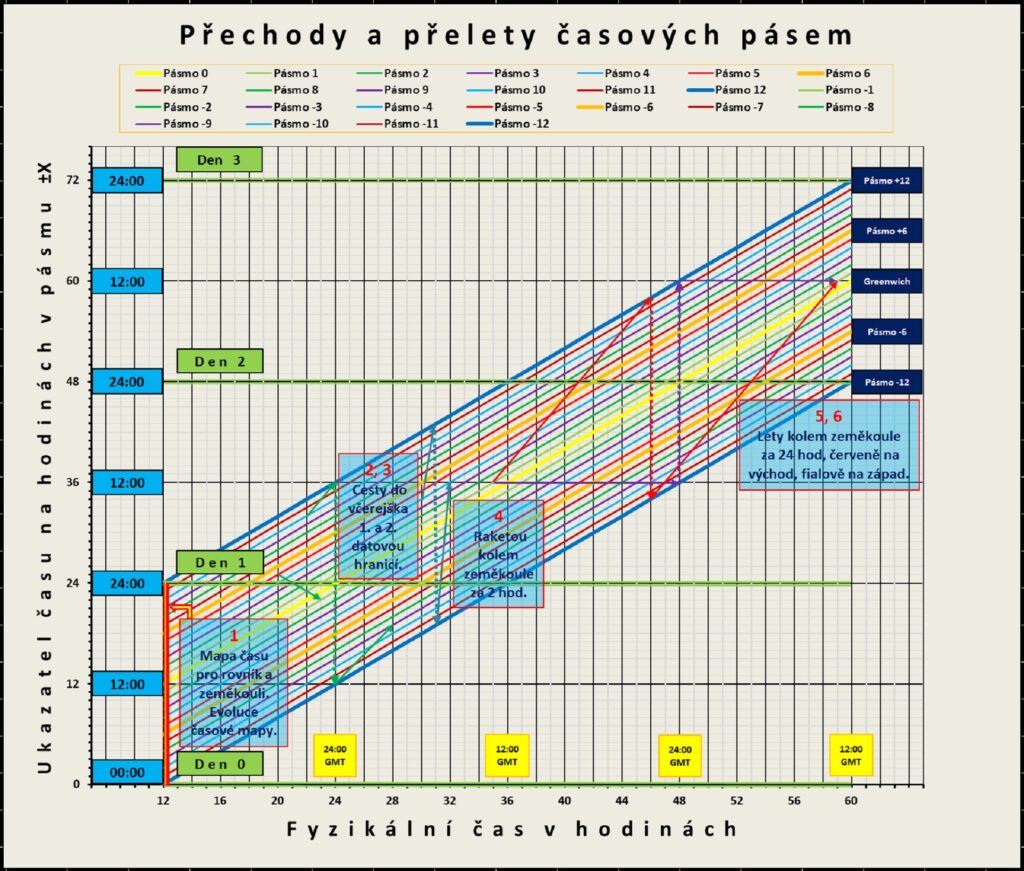
Výše zobrazené pohyby objektů (letadlo, raketa) jsou kreslené jako přímky, tj. předpokládají rovnoměrný pohyb, ale reálně to mohou být i křivky. Také jsou zde zobrazované jako spojitě mapované. V systému skokového mapování s časovými pásmy by to byly „zubaté přímky“ s malými pohyby po nakreslených pásmových časových přímkách a jednohodinovými skoky mezi přímkami trvající Δt_x = 0. Pro velké cesty a výpravy kolem Země mezi mnoha pásmy by bylo zbytečné zde zakreslovat jednotlivé malé skoky. Stačí vědět, že tam jsou, ale při nějakém podrobném záznamu cesty (letu, výpravy) by tato přesnost mohla být užitečná.

Přechod první datovou hranicí zde reprezentuje skok z pásma +12 do pásma -12 (a opačně), přechod druhou datovou hranicí je přechod zelenou přímkou oddělující dny (24 hod).

Evoluce plochy času – křivka 1

Úsečka 1 zobrazuje každý bod povrchu Země jako časovou souřadnici (na ose y) daného prostorového bodu v daný okamžik t_x (osa x). Všechny rovnoběžky tvoří stejnou časovou úsečku jako rovník. Poledník (s jediným stejným mapovaným časem pro všechny své body) tvoří jeden jediný bod úsečky.

Vzhledem k tomu, že jak severní, tak jižní pól tvoří bod, kde se všechny poledníky spojují, nacházíme další dva kostlivce. Pro oba tyto body totiž platí celá úsečka se všemi možnými nejednoznačnými časy. To je situace, kterou matematické funkce zrovna nezbožňují. Naštěstí libovolně malá kružnice kolem pólu je zobrazena stejnou časovou úsečkou jako rovník. Pólům tedy limitně patří celá úsečka což odpovídá realitě, protože na pólu platí všechny mapované časy zároveň a lidé z výzkumných stanic si musí některý z časů zvolit jako čas pro svoji komunikaci nejvhodnější.

Body podél poledníku mají ve všech polohách pro dané t_x pouze jeden čas t_y (ten je funkcí času na ose x), proto se všechny body podél poledníku (pohybující se po povrchu zeměkoule nebo ne) v čase pohybují podél příslušných pásmových časových přímek, nezávisle na měnící se zeměpisné šířce. Pohyby podél poledníku se na grafu nijak neprojeví.

t_x reprezentuje fyzikální čas, takže časy podél pásmových časových přímek jsou lokálně, tj. v rámci dané přímky fyzikální (Δt_x = Δt_y).

Objekty, které se pohybují podél rovníku nebo jiné rovnoběžky jsou zobrazené přímkou (obecně křivkou), jejíž směrnice se od směrnice pásmových časových přímek liší v závislosti na rychlosti a směru pohybu. Při pohybu na východ je směrnice dané křivky větší než směrnice pásmových časových přímek. S rostoucí rychlostí pohybujícího se tělesa se směrnice křivky zvětšuje.

Při pohybu na západ je směrnice dané křivky menší než směrnice pásmových časových přímek. I tady se s rostoucí rychlosti pohybu odchylka od pásmových křivek zvětšuje, tj. směrnice je stále menší až záporná. Pro tyto pohyby na východ nebo na západ platí, že časy na ose y už neodpovídají času na ose x (Δt_x ≠ Δt_y), proto časy na ose y takto se pohybujících objektů už nejsou fyzikální, obsahují součet reálné a virtuální mapovaně složky.

Obecně pro křivky času na grafu je možné říci, že časy jsou lokálně (v rámci „vnitřního prostoru“ pásmových časových křivek) fyzikální, ale globálně (v rámci všech křivek) ne-fyzikální, protože obsahují virtuální mapovanou složku času, která se v rámci „vnitřního prostoru“ pásmové časové křivky neprojeví.

Cesty do včerejška druhou datovou hranicí – křivka 2

Druhá datová hranice je reprezentována vodorovnou zelenou přímkou. Přechod druhou datovou hranicí na grafu znamená v běžném životě především přirozený vstup do nového dne vodorovnou zelenou „denní“ přímkou oddělující každých 24 hodin. Výpočetně je to přechod číslem 24:00, kdy začínáme opět nulou důsledkem periodického cyklu. Přechod datovou hranicí znamená začátek nového dne o půlnoci, následné svítání a východ Slunce.

Velmi rychlé lety směrem na západ, pokud dokážou překonat rychlost rotace, mohou formálně letět „i do včerejška“ (viz křivka 2). Jak je ale z grafu vidět, do včerejška můžeme cestovat jen u virtuálních časů, u skutečných fyzikálních časů ne.

Přechod do včerejška 2. datovou hranicí (křivka 2)
Start: pásmo +5, místní čas 1:00, den 1, GMT 20:00
Let: 3 hodiny
Cíl: pásmo -1, místní čas 22:00, den 0, GMT 23:00
Výpočet: 1:00 + 3 hod_fyz – 6 hod_map = 22:00 místního času a předchozí (nultý) den.

Rychlost letadla na 50. rovnoběžce (délka 25 728 km, pásmo 1072 km): 2 144 km/hod
Rychlost letadla na rovníku (délka 40 075 km, pásmo 1670 km): 3 340 km/hod
U výpočtu předpokládáme pro jednoduchost let z centrálního poledníku na centrální poledník.

Cesty do včerejška první datovou hranicí – křivka 3

Letem na východ je možné cestovat do včerejška jedině přechodem první datové hranice (IDL), viz křivka 3. Do předchozího dne přechází i zde pouze virtuální mapovaná složka času, reálná má vždy jen jeden směr, zleva doprava, z minulosti do přítomnosti, a pak do budoucnosti.

Přechod do včerejška 1. datovou hranicí (IDL), křivka 3
Start: pásmo +10, místní čas 8:00, den 1, GMT = 22:00
Přechod IDL: 12:00 místního času v pásmu +12, den 1, GMT = 24:00
Na druhé straně IDL: 12:00 místního času, den 0, GMT = 24:00
Cíl: pásmo -9, místní čas 19:00, den 0, GMT = 4:00
Let: celkově: 6 hod = 2 hod + 4 hod
Výpočet: 8:00 + 2 hod_fyz + 2 hod_map – 24 hod_map + 4 hod_fyz + 3 hod_map = 19 hod – 24 hod = 19 hod, den 0 (předchozí den).

Raketou kolem Země za 2 hodiny – křivka 4

V tomto případě jde o let rakety, která obletí zeměkouli za 2 hodiny. I když raketa přeletí datovou hranici, datum se nezmění. Raketa startuje z pásma +4 v čase 10:00, za dvě hodiny (po obletu Země) se vrací na stejné místo v čase 12:00 ve stejný den.

Start: pásmo +4, místní čas 10:00, den 1, GMT = 6:00
Přechod IDL: 19:00 místního času v pásmu +12, den 1, GMT = 7:00
Na druhé straně datové hranice: 19:00 místního času, den 0, GMT = 7:00
Cíl: pásmo +4, místní čas 12:00, den 1, GMT = 8:00
Let: celkově: 2 hod = 1 hod + 1 hod
Výpočet: 10:00 + 1 hod_fyz + 8 hod_map – 24 hod_map + 1 hod_fyz + 16 hod_map = 12 hod_fyz + (24 hod_map – 24 hod_map), 1. den

Den se nezměnil přesto, že raketa obletěla Zemi a prošla i mezinárodní datovou hranicí (IDL). Odečtené mapované složky času se přeletem časových pásem opět přičetly. Příklad je zajímavý tím, že při neuváženém uplatnění pravidla přeletu mezinárodní datové hranice by se jejím přeletem směrem na východ měl jeden den odečíst. To se také ve výpočtu udělalo, ale odečtení dne funguje správně jen pokud se při letu jednotlivé mapované složky v rámci skokového mapování také přičítají, jinak následuje chybný závěr, že se raketa přeletem datové hranice dostala do včerejška.

Původní pravidlo o Mezinárodní datové hranici funguje v základním tvrzení jen pro velmi pomalé cesty kolem Země, pro které bylo vytvořeno. Pokud výpravy trvaly týdny, měsíce nebo dokonce roky, tak se mapované složky času přičítaly nepozorovaně a neuvědoměle samé, každodenním měřením času na lodi. Pak stačilo den už jen odečíst, nebo přičíst (podle směru cesty), ale dnes už se všichni řídí centrálním časem a nikdo si ho neměří sám podle Slunce.

Druhou datovou hranicí raketa neprošla přesto, že na grafu „Evoluce plochy času…“ protla zelenou přímku. Druhou datovou hranicí se prochází jen v čase 24:00 příslušného pásmového času. Podrobněji v dalším textu níže. Z grafu je také vidět, že raketa neletí z místa startu po první datovou hranici, a pak od datové hranice dál, až do místa startu stále stejnou rychlostí. Za první hodinu přeletí 8 pásem, ale za druhou hodinu přeletí 16 pásem. Směrnice příslušných přímek proto nejsou stejné.

Letadlem kolem Země za 24 hodin, směr východ – křivka 5

Let letadla kolem Země za 24 hodin směrem na východ byl velmi podrobně popsán ve studii o Datové hranici. Zde se jedná jen o grafické zobrazení. Letadlo odlétá z Prahy z pásma +1 ve 12:00 SEČ (GMT 11:00). Graf zobrazuje přechod do nového dne ve 24:00 místního času v pásmu +7 (18:00 SEČ, GMT 17:00), dále přelet mezinárodní datové hranice v 10:00 místního času v pásmu +12 (23:00 SEČ, 22:00 GMT), kdy se čas skokově „zbavuje“ mapovaných složek času jako had staré kůže a přechází do 10:00 místního času v pásmu -12, ale předchozího dne. V dalším letu čas mapované složky opět získává. Letadlo znovu přechází do nového dne ve 24:00 v pásmu -5 a nakonec dorazí do cíle v pásmu +1 ve 12:00 SEČ.

Letadlem kolem Země za 24 hodin, směr západ – křivka 6

Let letadla kolem Země za 24 hodin směrem na západ byl také popsán ve studii o Datové hranici. Grafické zobrazení přesto umožňuje ještě jiný pohled. Letadlo odlétá z Prahy ve 12:00 SEČ (GMT 11:00). Graf zobrazuje „příchod“ nového dne ve 12:00 místního času získaný přeletem mezinárodní datové hranice z pásma -12 do pásma +12 po 13 hodinách letu a následný přílet do Prahy za dalších 11 hodin. Ve 12:00 místního času (tam, kde letadlo momentálně opravdu je) samozřejmě žádný den ve smyslu nového východu Slunce nepřichází, nový den na 2. datové hranici nastává jen ve 24:00 místního času, do měření se jen zavádí po 13 hodinách letu oprava na 1. datové hranici v rámci daného systému měření. Normálně by nový den v rámci SEČ (start byl ve 12:00) nastal už po 12 hodinách, tj. o půlnoci.

Současný přechod obou datových hranic

Za určité konstelace může nastat současný nebo téměř současný přechod obou hranic, tj. přechod hranic krátce po sobě. Tato situace je zajímavá tím, že v jednom případě (na obrázku vlevo) nastává znovu stejný den a ve druhém případě následuje skok o dva dny (na obrázku vpravo).

Přechod druhou datovou hranicí nastává vždy v reálném fyzikálním čase, tzn. že čas překonává hranici 24 hodin a mění se z hodnot 24 – ε na 24 + ε (pro ε > 0) kontinuálně, spojitě. Protože osa y obsahuje směs fyzikálního a mapovaného času, může se měnit i opačně z hodnot 24 + ε na 24 – ε. Potom nastává přechod do včerejška. Přechod 1. datovou hranicí se odehrává naopak jen v čase t_x = 0 a nastává jako virtuální časový zlom o 24 hodin. Tento přechod může nastat v libovolném čase, nejen o půlnoci, ale třeba v 10:00 dopoledne.

Téměř současný přechod první i druhou datovou hranicí tvoří 4 kombinace (viz obrázek), které jako dvojice 2+2 (v jedné variantě projdeme nejdříve 1. datovou hranicí a pak 2. datovou hranicí, ve druhé variantě opačně) splňují už dříve zmíněná schémata pro součty dní (1+1) a (1-1), viz Datová hranice. Celkový výsledek zobrazuje červená čára, která ukazuje, že v prvním případě na konci jednoho dne skočíme znovu na jeho začátek a ve druhém přeskočíme najednou dva dny.

V prvním případě je na obrázku vlevo nový začátek stejného dne. V čase GMT = 12:00, kdy začíná na Zemi v pásmu +12 nový den, tj. ve 24:00 místního času, můžeme přechodem IDL směrem na východ (z pásma +12 do pásma -12) skočit do stejného dne (z jeho konce na jeho začátek).

Je to přechod obou datových hranic, schéma (1-1), tj. den – den. Pokud by nám například nevyšlo pracovně nebo soukromě pondělí v pásmu +12, je možné si ho přechodem IDL o půlnoci ještě zopakovat znovu v pásmu -12 s už lepšími výsledky. Možné jsou dvě varianty krátce po sobě, buď jako (-1+1) nebo jako (1-1). V limitě to bude jeden přechod zobrazený červenou šipkou.

Ve druhém případě na obrázku vpravo se jedná o dvě varianty přechodu (1+1), tj. den + den, jedním nebo druhým směrem. Opět je to v limitě přechod zobrazený červenou šipkou. V tomto případě procházíme IDL směrem na západ.

Plochy času a matematické vztahy

Několik základních pravidel

↓↑
Pohyb mezi virtuálními mapovanými časy je možný v obou směrech. Přechod (přelet) mezinárodní datové hranice je na grafu prezentován virtuálním skokem (mezi pásmem -12 a pásmem +12) o 24 hod_map jedním nebo druhým směrem v čase Δt_x = 0. Podobně se uskutečňují skoky mezi časovými pásmy o 1 hodinu. To ale neznamená, že je možný libovolný pohyb v ose y. Například virtuální skok o jedno pásmo je možný na hranici dvou pásem, ale virtuální skok o dvě a víc pásem už ne, protože mimo IDL je možné virtuálně skočit jen o jedno pásmo.

Protnutí druhé (zelené) datové hranice na grafu „25 přímek“ kolmou šipkou znázorňující skok na 1. datové hranici (s výjimkou současného přechodu obou hranic) neznamená přidání ani odebrání dne z důvodu přechodu 2. datové hranice. Průsečík zelené (2. datové) hranice a virtuálního skoku o 24 hodin na 1. datové hranici je jen symbolický a ke skutečnému kontaktu obou hranic nedochází.

Druhou datovou hranici je možné překročit jen v místním čase 24:00 hod. Naopak, v konfiguraci na obrázku výše je časový přechod první datové hranice druhou viditelný jako průsečík dvou přímek. Najednou v pásmu +12 i v pásmu -12 nastává nový den, ale oba začátky jsou posunuté o 24 hodin.

→
Změna skutečného fyzikálního času je možná jen jedním směrem (v opačném směru ← ne).

Plochy času a směrnice pásmových časových přímek
Pohyb v rovině xy obecně: Δt_y = Δt_x + Δt_map, směrnice jsou větší nebo menší než 1, dle znaménka mapovaného času.
Pro pásmové časové přímky platí: Δt_map = 0.
Potom Δt_y = Δt_x To znamená, že směrnice pásmových časových přímek = 1.

Výpočet Δt_map a výsledného času na hodinách, které zohledňují polohu středního Slunce na obloze

Výpočet Δt_map (posunu času důsledkem změny polohy tělesa) a výsledného času na hodinách, které zohledňují polohu Slunce na obloze bude proveden pro spojité mapování z důvodu jednoduchosti matematických vztahů. Při skokovém mapování s „časovými pásmy“ to bude pohyb času s přískoky, kdy čas v rámci pásma plyne normálně a očekávaně, tj. spojitě a na hranici nového pásma poskočí o příslušnou pásmovou konstantu jedním nebo druhým směrem.

Nejdříve je třeba vypočíst, jak se posune mapovaný čas důsledkem změny polohy tělesa na ploše času, tzn. čas odpovídající pohybu tělesa rychlostí v podél rovnoběžky po dobu Δt_fyz. Potom se musí dát do vztahu mapované a fyzikální složky času. Výsledný čas bude udávat časový údaj na hodinách, které měří „spojitý lokální sluneční čas“ (SLSC) jako čas podle abstraktního středního Slunce nad hlavou. Tento čas přibližně odpovídá i pravému Slunci, ale není to pravý lokální čas měřený podle pravého Slunce. Je to abstrakce vyhlazující různé nerovnoměrnosti.

Δt_SLSC = Δt_fyz ± Δt_map, znaménko se mění podle toho, zda jdeme na východ (+) nebo na západ (-)

Pokud 15⁰ odpovídá 1 hod_map, pak x⁰ odpovídá Δt_map

Δt_map (hod_map) = Δx⁰/15⁰ , kde Δx⁰ je úhel, o který se otočí Země za čas Δt_fyz, tj. za dobu pohybu tělesa podél rovnoběžky. Zde nastává na začátku článku popsaná situace, že čas v jedné situaci fyzikální je v jiné mapovaný.

Pokud 2πr délky odpovídá 360⁰, pak v * Δt_fyz odpovídá posunu Δx⁰ podél rovnoběžky, kde r je poloměr rovnoběžky a v rychlost tělesa v daném směru.

Δx⁰ = [(v * Δt_fyz)/(2πr) ] * 360⁰, po dosazení

Δt_map = [(v * Δt_fyz )/(2πr)] * 24, po dalším dosazení

Δt_SLSC = Δt_fyz * (1 ± (v * 24)/(2πr)) pro spojitý lokální sluneční čas měřený podle středního Slunce resp. dnes už spíše podle abstraktního „atomového Slunce“ jako UTC s atomovou sekundou.

Jedná se o čas v hodinách jako jednotkách času, který obsahuje směs mapovaných a fyzikálních složek času. Plyne na hodinkách při jejich pohybu rychlostí v na povrchu plochy času podél rovnoběžky. V kolmém směru, podél poledníku, je mapovaná složka času nulová, Δt_map = 0.

R je poloměr Země, r je poloměr rovnoběžky, r = R*cos φ, kde φ je zeměpisná šířka.

Obecný vztah pro plynutí času pohybujících se těles po plochách času

Jednorozměrné mapování

Proces mapování probíhá jen v jednom rozměru, ve směru kolmém je nulový. To platí například pro plochy času rotující zeměkoule a tělesa, která se po zeměkouli pohybují běžnými rychlostmi (auta, letadla, lodě, chodci).

Výpočet

Pokud Δt_0map odpovídá změně času na vzdálenosti Δx_0map, pak Δt_map je mapovaný čas odpovídající vzdálenosti Δx.

Δt_map = Δt_0map * Δx/Δx_0map

v * Δt_fyz = Δx

Δt_SLSC = Δt_fyz * (1 ± v * Δt_0map/Δx_0map)

Pokud zavedeme rychlost mapování jako v_map = Δx_0map/Δt_0map, pak

Δt_SLSC = Δt_fyz * (1 ± v/v_map)

Jedná se o plynutí času, který běží na hodinkách při pohybu tělesa rychlostí v po povrchu plochy času ve směru mapování (+), nebo v protisměru (-).

Příklady zajímavých změn chodu času na hodinkách

Platí: Δt_SLSC = Δt_fyz * (1 ± (v * 24)/(2πr))

Letadlem kolem Země za 24 hodin podél rovnoběžky o poloměru r

Na východ
v_L * 24 = 2πr, v_L je rychlost letadla
Δt_SLSC = Δt_fyz * (1+1) = 2 * Δt_fyz, čas běží 2x rychleji než fyzikální

Na západ
v_L * 24 = 2πr, v_L je rychlost letadla
Δt_SLSC = Δt_fyz * (1-1) = 0, čas na hodinách se zastavil (aby hodinky s baterkou šly dobře, musíme vyjmout baterku).

Urychlení a zpomalení času

Cesty na východ znamenají urychlení času, cesty na západ zpomalení času měřeného dle SLSC hodinek.

Δt_SLSC = Δt_fyz ± Δt_map, jednou se mapovaní složka času přičítá, a podruhé odečítá.

Zamrzlý čas

v_L * 24 = 2πr
Δt_SLSC = Δt_fyz * (1-1) = 0, čas na hodinách se zastavil

Pokud se pohybujeme stejnou rychlostí jako je rotace Země proti směru rotace, Slunce je nad hlavou a tomu odpovídající čas se zastaví.

Δt_SLSC = Δt_fyz – Δt_map = 0

Δt_fyz = Δt_map, úbytek mapovaného času ruší přírůstek fyzikálního.

Zpětný chod času

Pokud (v_L * 24)/(2πr) = ε > 1, tj. pohybujeme se rychleji než rotace Země, tak při cestování v protisměru mapování Δt_SLSC = Δt_fyz * (1 – ε), kde ε > 1, je tok času je záporný, záporná složka mapovaného času převládla nad složkou fyzikálního času. V takovém případě cestujeme „do minulosti“, ale vzhledem k rozsahu mapovaného času od 0 do 24 hodin můžeme reálně (v systému měření na Zemi) cestovat jen do včerejška a dál už ne. Cestování je samozřejmě pouze formální (dle SLSC hodin), necestujeme do minulosti ve fyzikálním čase.

Magellan a výpravy kolem Země

v * 24 * k = 2πr, k je počet dní, které trvá výprava kolem Země (třeba 1000 dní)
Δt_fyz = k dní
Δt_SLSC = k * (1 ± 1/k), jemné zpomalení nebo urychlení času
Δt_SLSC = k ± 1, (+ na východ, – na západ). Na východ musíme den odečíst, protože SLSC hodiny naměří o den víc (právě tohle jsou „zprůměrované“ hodiny námořníka Magellanovy výpravy). Na západ musíme den přičíst, protože SLSC hodiny naměří o den méně. Pak dostaneme normální fyzikální čas a tomu odpovídající počet k dní.

Poznámka na závěr
Manipulace s časem zde znamenají jen manipulace se systémem jeho měření, jsou to „kouzla“ s hodinkami, ne s fyzikálním časem.

Plochy času v rovině kolmé na rovinu evoluce

Frontální plocha na grafu je momentka v čase t = t₀ = 12 hod. Reálný čas zde neběží, jde o „foto“ časových souřadnic promítnutých na povrch Země. Osa z udává úhly zeměpisné šířky a kolmice jsou rovnoběžky kolem Země příslušné k dané zeměpisné šířce φ ve stupních. Ypsilonová souřadnice udává čas a tím i polohu, protože tyto veličiny jsou svázané. Pro každý čas t jsou souřadnice 6 hod, 12 hod, 17 hod …, zároveň souřadnicemi zeměpisné délky a určují v rámci evoluční křivky, kde se daný bod nachází. Zobrazení (přiřazení) času a polohy může fungovat jako spojité i skokové.

Protože souřadnice jsou uvedené v hodinách, tj. veličinou času, rovnoběžky jsou v časových souřadnicích stejně velké od rovníku až po pól s celkovým rozsahem 24 hod. Každou rovnoběžku tak roztáhneme na délku rovníku a dostaneme plochu reprezentující povrch celé zeměkoule. Libovolně malá kružnice kolem pólu je zobrazena stejnou časovou úsečkou jako rovník, protože má stejný časový rozsah.

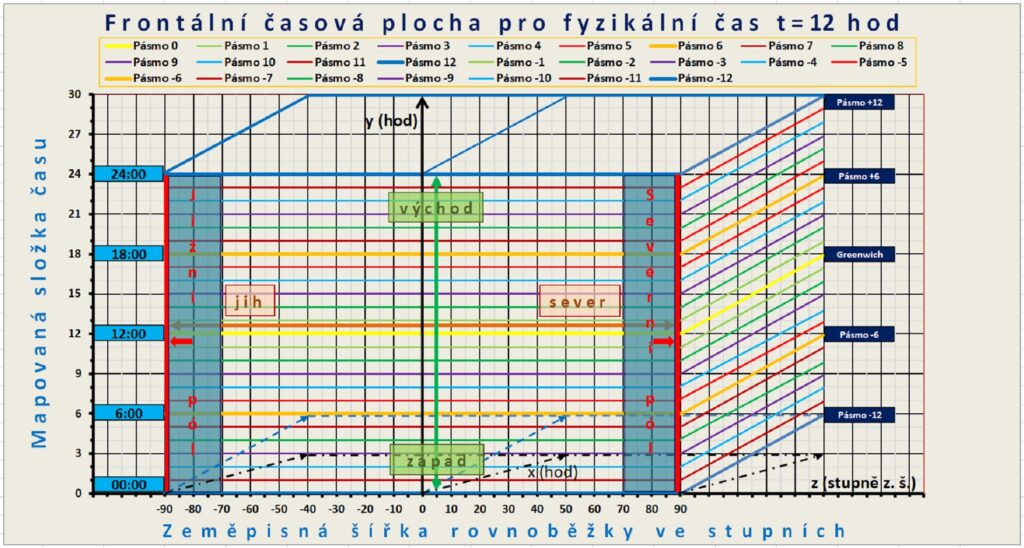
Samotný pól je úsečka, která znamená, že jednomu bodu přísluší všechny časy zároveň. Tak je to i ve skutečnosti, kde zeměpisný pól je jen jeden geometrický bod. Pólu jsou přiřazené všechny mapované časy v daném okamžiku najednou, ale libovolně malá rovnoběžka kolem pólu má už jednoznačně přiřazené časy všem bodům svého obvodu.

Protože na celé frontální ploše platí, že Δt_x = 0, Δt_y v této situaci reprezentuje jen virtuální mapovanou složku času Δt_y = Δt_map a fyzikální čas je roven konstantě. Pohyb kolmo dolů ↓ reprezentuje změnu polohy po rovnoběžce směrem na západ (virtuální čas ubývá), pohyb kolmo nahoru ↑ reprezentuje pohyb po rovnoběžce na východ (virtuální čas přibývá). Rovnoběžky jsou zde kolmice.

Pohyb vpravo → znamená pohyb po poledníku směrem na sever, pohyb vlevo ← znamená pohyb po poledníku směrem na jih. V obou případech je změna Δt_map = 0. Poledníky jsou zde vodorovné přímky.

Pohyb po rovnoběžce na východ na frontální ploše ↑
Δt_y = Δt_map nenulová hodnota virtuálního času = kladné hodnotě
Promítnuto do reality, tj. do času t: Δt_y = Δt_map + Δt_x
Směrnice přímky v rovině xy: (Δt_y/Δt_x) = 1 + Δt_map/Δt_x = 1 + ε/Δt_x ˃ 1, kde ε > 0
Jde o shodu s výsledky grafu „let letadla za 24 hod“ směr východ v ose xy, kde byla směrnice větší než směrnice pásmových časových přímek.

Pohyb po rovnoběžce na západ na frontální ploše ↓
Δt_y = Δt_map nenulová hodnota virtuálního času = záporné hodnotě
Promítnuto do reality, tj. do času t: Δt_y = Δt_map + Δt_x
Směrnice přímky v rovině xy: (Δt_y/Δt_x) = 1 + Δt_map/Δt_x = 1 + ε/Δt_x ˂ 1, ε ˂ 0
Jde o shodu s výsledky grafu „let letadla za 24 hod“ směr západ v ose xy, kde byla směrnice menší než směrnice pásmových časových přímek.

Zvláštní případy letu na západ s Δt_map ˂ 0
0 ˂ 1 + Δt_map/Δt_x ˂ 1
0 = 1 + Δt_map/Δt_x ˂ 1 (let letadla za 24 hod kolem zeměkoule směrem na západ)
0 ˃ 1 + Δt_map/Δt_x ˂ 1

Pokud je směrnice křivky (1 + Δt_map/Δt_x) v rovině xy větší než nula, čas měřený podle Slunce je jen zpomalen. V případě, že směrnice křivky je v rovině xy rovna nule, sluneční čas zamrznul a hodinky stojí.

Pokud je směrnice křivky menší než nula, tj. záporná (na grafu je to křivka číslo 2), čas běží zpět. Znamená to zajímavou situaci: (- Δt_map)/Δt_x ˃ 1 aneb (- Δt_map) ˃ Δt_x.
Virtuální složka času roste (v absolutních hodnotách) rychleji než reálná. Na časových plochách je ale Δt_x svázáno s rotací Země, ta formálně určuje ve zvoleném modelu chod času pro každý bod povrchu Země, viz Mapování času.

Virtuální složka je svázána s geometrií kružnice, resp. koule, proto její změnu způsobuje pohyb po povrchu Země (tj. změna polohy),jinak je pro dané konkrétní místo konstantní. To znamená, že letadlo (letící proti rotaci Země) odpovědné za rychlost plynutí mapovaného času má větší rychlost než je obvodová rychlost na povrchu zeměkoule od rotace Země, která je odpovědná za změnu (plynutí) fyzikálních časových souřadnic. Proto čas na hodinách běží směrem zpět.

Uzavřené plochy času a periodicita času

Plochy času by neobsahovaly první datovou hranici, pokud by nebyly uzavřené jako kružnice, válec nebo koule. Tyto uzavřené plochy jsou na grafech „rozbalené“ do roviny, ale ve skutečnosti se horní a dolní kraj plochy navzájem dotýkají, a právě tato linie související s uzavřeností a periodicitou tvoří 1. datovou (časovou) hranici. Jinak čtverec nebo obdélník, reprezentující časovou plochu a pohybující se v čase, žádnou datovou, tj. časovou hranici mít nemusí.

Právě inverzní operace k mapování, tj. přechod první datovou hranicí s přičtením, nebo odečtením dne, zajišťuje periodicitu. Je to podobné jako, když na hodinkách po 24 hodinách, tj. přechodem 2. datové hranice, začínáme (s uplatněním periodicity) opět nulou. V takovém případě ale násobky 24 hodin nezahazujeme, ale naopak zapisujeme do kalendáře. Násobky 24 hodin v podobě dnů potřebujeme v záznamech, abychom věděli, kolik času uplynulo.

Tady se v cyklech přidaného „virtuálního“ času zbavujeme jako had staré kůže, nic se nezaznamenává. Násobky 24 hodin jdou na 1. datové hranici jako zcela bezcenné do koše po každém cyklu pohybu po uzavřené časové ploše. V tom je podstatný rozdíl mezi 1. a 2. datovou hranicí.

Plochy času, spojité a skokové změny času

Následující obrázek je zvětšenina části prvního základního obrázku „25 přímek“, který zobrazuje evoluci plochy času a umožňuje zobrazovat schémata pohybu těles po povrchu zeměkoule. Dokreslené jsou černé přímky hranic časových pásem, naopak zde chybí časové osy, protože obrázek je jen výřez grafu. Časové osy jsou stejné jako na základním obrázku. Čtverce (časová síť) definují jak na ose y, tak na ose x hodinové úseky. „Vzdálenost“ barevných přímek, kde probíhá čas centrálních poledníků je jedna hodina, „vzdálenost“ černých přímek zobrazujících hranice časových pásem je také 1 hodina. Na obrázku je vidět princip časových skoků při pohybu tělesa ve srovnání se spojitým průběhem pohybu i času.

Důležitým faktem je, že skokové mapování vymaže informaci o poloze tělesa. Jedinou informací je, že se těleso nachází v daném časovém pásmu, ale nepoznáme ani z. š., ani z. d.

Při spojitém mapování se na ploše odehrává spojitý reálný pohyb zobrazený v promítnutých časových souřadnicích. Při skokovém mapování probíhá čas v rámci jedné části časové plochy (ohraničené hranicemi příslušného časového pásma) výlučně podél barevné pásmové časové přímky. Tento čas je normální – fyzikální a je v něm možné zobrazovat pohyby těles. Při přechodu hranice pásma čas skočí o 1 hodinu směrem nahoru nebo dolů a získá „vstřebe do sebe“ další mapovanou složku času, která je reprezentována rozdíly na ose y pro daný fixní čas na ose x. Po skoku čas pokračuje ve svém „plynutí, evoluci“ podél další příslušné pásmové časové přímky.

První časová křivka zobrazuje už probíraný let letadla kolem Země za 24 hodin směrem na západ. Červená přímka zobrazuje spojité mapování a „zamrzlé“ hodinky. Oranžová zubatá křivka ukazuje čas na klasických pásmových hodinách druhého pilota, kterému čas cykluje při letu stále v intervalu 11:30 až 12:30.

Druhá časová křivka je let letadla směrem na východ s obletem Země za 24 hodin. Druhému pilotovi letí čas 2x rychleji než prvnímu a za 3 hodiny na hodinkách prvního pilota uběhne druhému 6 hodin. To se opraví později na 1. datové hranici (IDL), kde proběhne „časový servis“ spojený s úklidem veškerého časového harampádí.

Třetí časová křivka ukazuje složitější pohyb, kdy se těleso pohybuje trochu „chaoticky“, jednou rychleji a jindy zas pomaleji. Projeví se to jako změny směrnice křivky. Při pohybu směrem na východ bude směrnice křivky v daném bodě větší než směrnice pásmových přímek, při pohybu na západ bude směrnice křivky v daném bodě menší než směrnice pásmových přímek. Pohyby po poledníku se v mapované složce času neprojeví. A protože se tato složka času nemění, bude platit, že Δt_y = Δt_x.

Plochy času a variabilní intervaly času

Variabilní intervaly času znamenají cyklické změny sklonu evolučních křivek , viz 1. část Studie časových systémů o Mapování času. Tyto změny jsou znázorněné v závěrečné části studie: Od stejných časových intervalů k variabilním. Na principu zobrazeném na jedné jediné křivce ilustračního grafu, by bylo na sebe navrstveno 25 evolučních křivek s odstupem mapovaného intervalu 1 hodina a s celkovým rozsahem mapovaného času 24 hodin.

Paradox časového skoku na datové hranici a pohyb po časové ploše

Pokud by se Země otáčela velmi pomalu (viz časový paradox z článku o Datové hranici) a jedna otočka by trvala 5 let (roční oběh kolem Slunce by byl také patřičně delší), bylo by zajímavé sledovat chod času podle stejného časového systému jako používáme dnes, tj. podle polohy Slunce na obloze. Z hlediska názornosti probereme nejdříve spojité mapování bez časových skoků.

Padesátá rovnoběžka má 25 728 km, jedno pásmo má 1072 km. Nová časová mapa by nakreslila na povrchu novou síť 43 824 poledníků vzdálených jeden od druhého 1 časovou hodinu. Metrická vzdálenost mezi nimi by na padesáté rovnoběžce byla 587 metrů. Znamená to, že pokud bychom leželi, seděli nebo stáli na jednom místě bez pohybu jako sochy, čas na hodinách by běžel „normálně“. Ale už při obyčejné běžné chůzi podél rovnoběžky (ve směru mapování) by se čas na 587 metrech změnil navíc o 1 přidanou mapovanou hodinu dopředu (nebo naopak dozadu při chůzi opačným směrem). Virtuální hodina by se přidávala (nebo odebírala) ke skutečnému času potřebnému na překonání vzdálenosti 587 m.

Běžná chůze rychlostí 5 km/hod znamená cca 1,39 m/s. Potom 587 metrů uděláme uvedenou rychlostí za cca 7 minut (422,6 s). Na vzdálenosti 1,39 m by se ale kvůli mapování času SLSC hodinky posunuly navíc o 8,52 sekundy. Po každé fyzikální sekundě by se k hodinám připočetlo nebo odečetlo dalších 8,52 sekund virtuálního mapovaného času. S trochou humoru by se dalo říci, že čas by „běžel rychlostí“ 9,5 s/s… Podle směru a rychlosti pohybu by to bylo někdy více a někdy méně, v kolmém směru by hodiny běžely normálně bez přidaného času (pohyb po poledníku) a při chůzi opačným směrem by hodiny šly opačně, tj. čas by běžel zpět. Na každých 1,39 m v protisměru mapování by „uplynulo“ -8,5 s. Zde by byla „výsledná rychlost“ „plynutí“ času – 7,5 s/s (opět s trochou nadsázky).

Se zvyšující se rychlostí pohybu (jízda autem) by hodiny šly stále rychleji. Není v tom žádná relativita, je to jen způsob tvorby časových souřadnic na základě pohybu Slunce po obloze.

Takto definovaný čas by byl naprosto nepoužitelný, takže by se musela provést stejně jako v 19. století standardizace s cílem zavést nějaká rozumná časová pásma. Možná by se povrch Země musel rozdělit na podobné plochy jako dnes a „malé“ posuny času (ve skutečnosti docela velké) by bylo nutné na hranici každého pásma shromáždit, sečíst a posunout čas najednou, skokem, v tomto případě nejlépe o celé týdny či měsíce (pokud uvažujeme v současných jednotkách). „Kvantování“ časové plochy by tu znamenalo jediný funkční čas reprezentovaný „spektrem“ podobných pásmových časových přímek jako používáme dnes, viz předchozí obrázky.

Výše uvedený příklad je modelový a ilustruje problematiku mapování času. Pokud by se Země opravdu otáčela 5 let, systém měření času na povrchu planety by se nejspíše musel definovat úplně jinak. Pravděpodobně tak, že na celém povrchu by byl jen jeden fyzikální čas. Čekat s dalším obědem na následující pravé poledne 5 let by vydrželo jen málo lidí. A možná by se uplatnily úplně jiné životní cykly a úplně jiné časové periody, ale to už sem nepatří.

***************

Konec 3. části

***************

1. část Studie časových systémů
Mapování času
2. část Studie časových systémů
Datová hranice
3. část Studie časových systémů
Plochy času
4. část Studie časových systémů
Správný čas

***************

Autor: Miloš Antes