Rovnice času aneb šílenství rychlostí, poloh a časů

Pro studium délky dne má zásadní význam tzv. „časová rovnice (rovnice času)“, proto je zde toto téma rozebráno velmi podrobně. Jedná se o poměrně komplikované vztahy nebeské mechaniky při oběhu Země kolem Slunce. Pochopit tuto rovnici znamená zjistit, jaké zákony a vztahy ovládají pohyby těchto dvou těles ve vesmíru a jak fungují. A rozhodně to není úplně triviální.

Nejde o exaktní odvození rovnic, které se nachází v astronomických učebnicích nebo odborných článcích, ale o intuitivní a názorný přístup k problému s minimem vzorců. Pojem časová rovnice (equation of time – rovnice času) má historickou tradici a znamená rovnost časových souřadnic E = T_P – T_S, kde T_P jsou souřadnice pravého Slunce a T_S souřadnice středního Slunce.

E je hodnota časového rozdílu, pokud poznáme tuto hodnotu (například z měření nebo z tabulek), můžeme ji připočítat k hodnotě středního času daného hodinkami a zjistíme, kdy nastává pravé poledne. Tato rovnice je v tabulkách měřená v diskrétních intervalech po 24 hodinách vždy v poledne, ale skutečný děj je spojitý, protože pravé a střední Slunce se pohybují i v čase mezi dvěma poledny.

Ve skutečnosti se jedná o 365 rovnic pro pravé a střední poledne v průběhu roku, které jsou průsečíkem času „poledne UT = 12:00“ na ose x, a jedné spojité funkce času E (t) na ose y. Funkce času E (t) udává neustále se měnící časový rozdíl mezi pravým a středním časem. Konkrétní hodnoty pro poledne jsou uvedené v astronomických tabulkách.  

Hlavní závěr kapitoly je, že žádný přesně 24hodinový sluneční den na Zemi neexistuje. Je to jen chiméra, přelud, kterému lidé věří. Skutečná délka dne, stejně jako pravé poledne, se mění poměrně složitým a dost nečekaným způsobem.

Tento text je volným pokračováním článku o délce dne:
https://zimnialetnicas.cz/delka-dne-na-zemi-aneb-od-setrvacniku-az-k-slunecnici/

Obsah

1. Úvod do problematiky rovnice času
   1.1 Několik astronomických pojmů
   1.2 Proti-otáčení
   1.3 Mapování času změnou geometrického úhlu
   1.4 Rovnice času a znaménková konvence
   1.5 Dvě složky rovnice času
2. První střední Slunce a funkce E₁
   2.1 Graf a data pro funkci E₁
   2.2 Obrázek pohybu Sluncí, který generuje časový rozdíl E₁
   2.3 Komentář k obrázku pohybu Sluncí a složce E₁ rovnice času
   2.4 Rychlosti pohybu Sluncí
   2.5 Proč by právě sinus mohl modelovat průběh funkcí E₁ a E₂
   2.6 Důležité charakteristiky pohybu Sluncí na hranicích oblastí
   2.7 Fázově posunuté střední Slunce (myšlenkový experiment)
3. Druhé střední Slunce a funkce E₂
   3.1 Promítání v prostoru a změna úhlu od 0⁰ do 23,5⁰
   3.2 Graf a data pro funkci E₂
   3.3 Obrázek pohybu Sluncí, který generuje časový rozdíl E₂
   3.4 Komentář k obrázku pohybu Sluncí a složce E₂ rovnice času
   3.5 Vzájemné relativní rychlosti Sluncí
   3.6 Nulové body funkce E₂
   3.7 Intuitivní konstrukce funkcí E₁ a E₂
4. Funkce času E = E₁ + E₂ a rovnice času E = T_P – T_S
   4.1 Graf a data pro funkci E
   4.2 Odchylky pravého poledne a pravého dne
   4.3 Je to funkce nebo rovnice? Platnost tabulky hodnot pro „rovnice času“
   4.4 Obrázek výsledného pohybu Sluncí, který generuje časový rozdíl E
   4.5 Komentář k obrázku pohybu Sluncí a funkci E
   4.6 Nejkratší a nejdelší den v roce, inflexní body funkce E
   4.7 Délka dne a odchylky od 24 hod graficky
   4.8 Rovnice času a matematické vyjádření délky pravého dne

1. Úvod do problematiky rovnice času

1.1 Několik astronomických pojmů

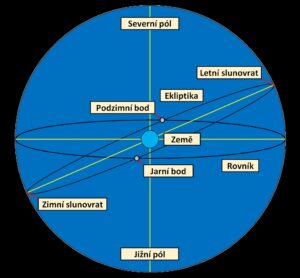
Nebeská sféra je koule na noční obloze, kde je pozorovatel uprostřed této koule na povrchu Země. Nebeský rovník je průmět rovníku Země na nebeskou sféru (průsečík roviny rovníku Země s nebeskou sférou). Ekliptika je průsečík roviny dráhy Země s nebeskou sférou. Z pohledu pozorovatele na Zemi se Slunce na obloze pohybuje právě po ekliptice. Průsečík ekliptiky a nebeského rovníku je jarní a podzimní bod. Jde o body, kde nastává rovnodennost. V těchto bodech svírá ekliptika a nebeský rovník 23,5⁰. Ekliptika i nebeský rovník jsou kružnice.

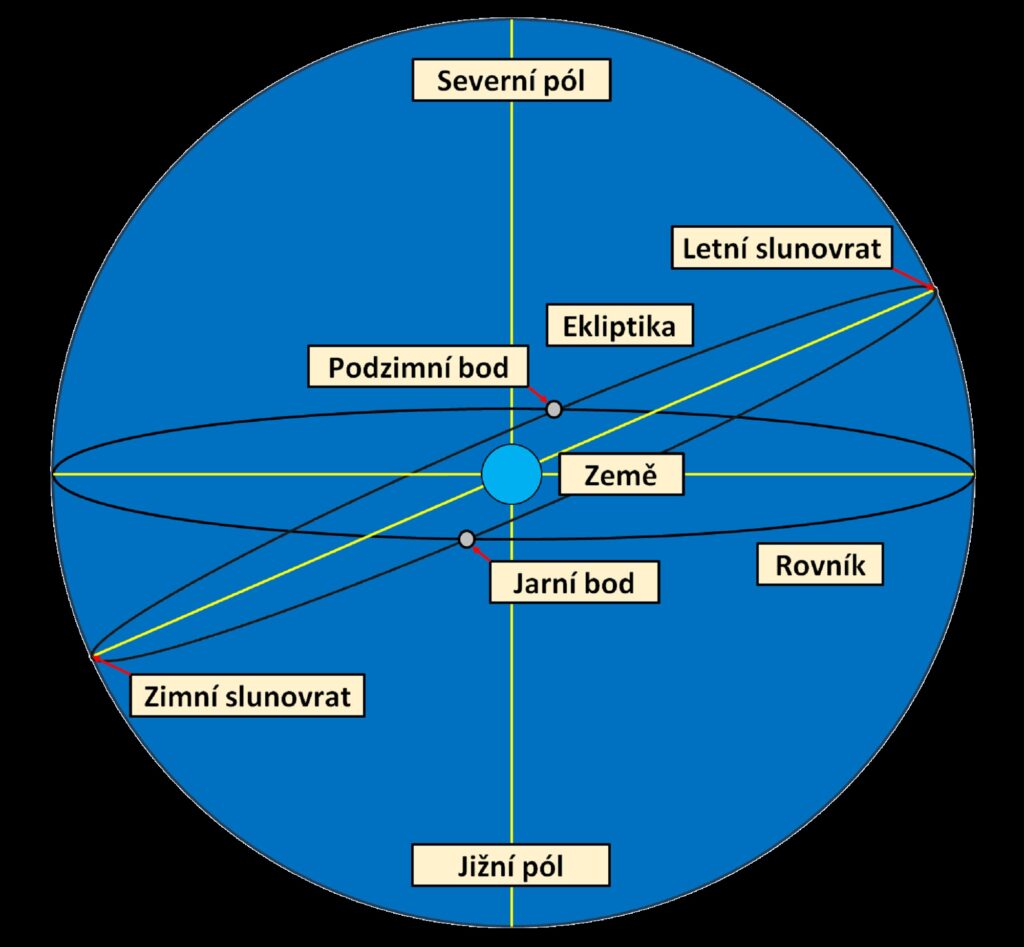
Nebeská sféra je nekonečně vzdálená sférická plocha, která se otáčí, protože Země rotuje. Hvězdy opisují kružnice a otočí se za 1 hvězdný den (23 hod 56 min 4 s). Slunce se pohybuje po tzv. ekliptice, 1 oběh trvá rok. Kružnice kolmé k rovině nebeského rovníku („nebeské poledníky“) se nazývají deklinačními kružnicemi. Podél deklinační kružnice se měří deklinace (tj. úhly „zeměpisné šířky“ na nebeské sféře, 0⁰ má nebeský rovník, 90⁰ severní pól, -90⁰ jižní pól.

1.2 Proti-otáčení

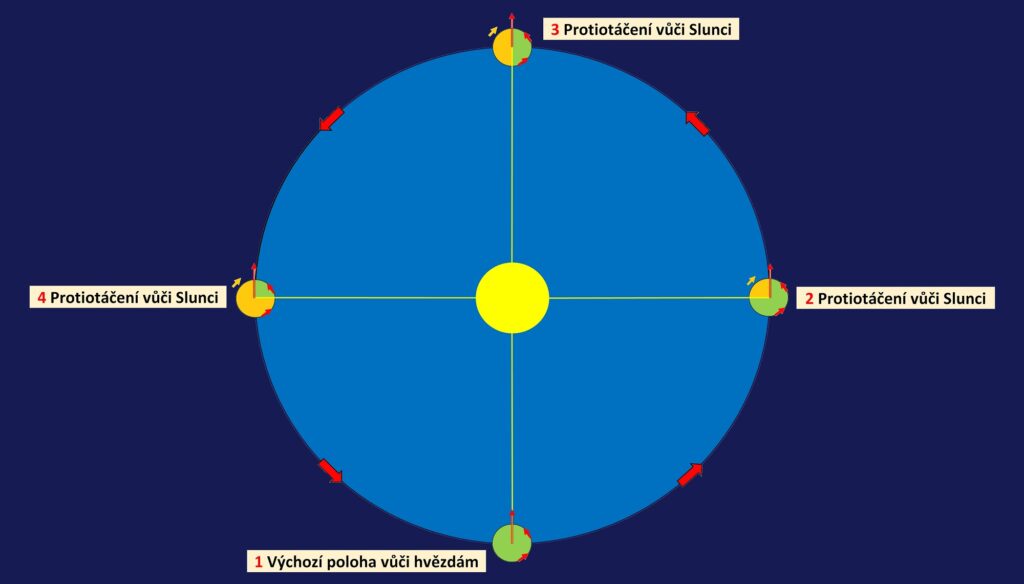
Proti-otáčení je hlavním zdrojem problémů při měření času podle Slunce. Samotné „setrvačníkové“ otáčení o 360⁰ vůči hvězdám je poměrně stabilní a s touto délkou dne ani pravým polednem by „skoro žádný“ problém nebyl (alespoň ne krátkodobě v rámci jednoho roku).

Různé rychlosti pohybu Slunce kolem Země se promítají právě do variabilního proti-otáčení. Jsou důsledkem Keplerových zákonů i měnících se úhlů při promítání pohybu Slunce z ekliptiky do roviny nebeského rovníku kolmé k ose otáčení. Tyto rychlosti a jejich průměty znamenají měnící se příspěvky k úhlům, pod kterými bychom jinak pozorovali Slunce, kdyby se Země kolem Slunce nepohybovala vůbec, pouze by rotovala. Až výsledné úhly (otočení vůči hvězdám + proti-otáčení) jsou tím, co mapuje sluneční časové souřadnice, tj. přiřazuje jednotlivým úhlům čas. Výsledný průběh takto mapovaného času je potom nerovnoměrný a musíme ho průměrovat, středovat.

1.3 Mapování času změnou geometrického úhlu

Čas musíme podle něčeho měřit a pravítkem se to dělat nedá. V jisté etapě lidského poznání to byl pohyb Slunce na nebi, podle kterého se měřil čas.

Pokud (z hlediska pozorovatele na Zemi) Slunce obíhá kolem Země, pak můžeme měřit úhel, pod kterým Slunce pozorujeme. Celkový úhel 360⁰ kolem rotační osy Země můžeme rozdělit na úseky po 15⁰ a čas, který uplyne mezi dvěma polohami Slunce, označíme jako hodinu.

Pokud nemáme jiné lepší srovnávací hodiny, tak nevíme, jak hodnotit rovnoměrnost pohybu Slunce a úhlům α₁, α₂, α₃, resp. Δα₁, Δα₂, Δα₃ bude příslušet „hodina“ času, i kdyby ta hodina „po našem“ trvala ve skutečnosti 3 hodiny. Čas tu měříme na základě zvolených astronomických dějů a geometrie úhlů. Podle zvoleného systému měření tak můžeme dostat různé (mírně odlišné) časové systémy.

V astronomii se úhlu α, resp. Δα, říká hodinový úhel. Je to úhel mezi místním nebeským poledníkem (meridiánem) a deklinační kružnicí zvoleného objektu na obloze (Sluncem, hvězdou). Jinak řečeno je to úhel mezi dvěma rovinami protínajícími se v ose rotace Země. Jednu určuje poledník, kde je pozorovatel a druhou rovina, kde je daný nebeský objekt. Hodinový úhel se měří od meridiánu, kde je definována nula ve směru zdánlivého pohybu hvězd, tj. směrem na západ. V okamžiku kulminace nebeského objektu (poledne) je hodinový úhel nulový, 15⁰ definuje hodinu (1⁰ jsou 4 časové minuty).

Takto je možné definovat na hvězdné obloze „hvězdný čas“ jako hodinový úhel jarního bodu nebo „sluneční čas“ jako hodinový úhel Slunce. Vznikají jakoby „různé časy“, které jsou ale ve skutečnosti jen souřadnice různých časových soustav a patří stejnému fyzikálnímu času.

Na základě pravého (skutečného) Slunce na obloze je definován pravý sluneční čas T_P (true solar time) jako hodinový úhel pravého Slunce. Z důvodu nerovnoměrnosti a nepřesnosti mu někdy říkáme zdánlivý sluneční čas (apparent solar time), protože vychází ze „zdánlivého“ pohybu Slunce na obloze. Výraz „zdánlivý“ není nejvhodnější, protože Slunce na daném místě oblohy opravdu vidíme (není to optický klam), ale poloha zahrnuje i proti-rotaci, tj. důsledky pohybu Země kolem Slunce.

T_S jsou souřadnice tzv. středního času. Ten je virtuální vystředovanou hodnotou, je to jen myšlenkový koncept, průměr všech dnů v roce. Žádné střední Slunce na obloze není. Z hlediska běžícího času můžeme za přístroj určující tento střední čas považovat přesné mechanické hodiny (problematiku „atomového“ času zde můžeme vynechat).

1.4 Rovnice času a znaménková konvence

E = T_P – T_S, to znamená, že T_P = T_S + E, kde

T_P jsou souřadnice pravého Slunce, T_S1 souřadnice 1. středního Slunce
T_S2 souřadnice 2. středního Slunce = T_S souřadnice středního Slunce

12:00_P = 11:57_S + 3 min, E > 0
12:00_P = 12:03_S – 3 min, E < 0

E > 0, pravý čas předchází střednímu (pravé poledne na obloze nastane dřív než střední), Země se „proti-otáčí“ pomaleji než je průměrné proti-otáčení a polohu z předchozího dne (např. poledne) dosahuje dříve než polohu středního Slunce. Dotočení Země vůči pravému Slunci (při konstantní rotaci) trvá kratší dobu než dotočení vůči „střednímu“ Slunci.

E < 0, pravý čas se opožďuje oproti střednímu (pravé poledne na obloze nastane později než střední), Země se „proti-otáčí“ rychleji než je průměrné proti-otáčení a polohu z předchozího dne (např. poledne) dosahuje později než polohu středního Slunce. Dotočení Země vůči pravému Slunci (při konstantní rotaci) trvá déle než vůči „střednímu“ Slunci.

V některých státech má parametr E opačné znaménko (E = T_S – T_P). Důsledkem je, že výsledné grafy této veličiny jsou vzhledem k hodnotám na ose y zrcadlově převrácené. Jinak je to samozřejmě jedno.

Pojem časové souřadnice je v této souvislosti nutné brát s jistou rezervou, protože pravé Slunce neudává rovnoměrný čas se stejnými intervaly. Na druhé straně i modernější měření vykazuje vždy nějakou nepřesnost. Neuvěřitelné je, že první úvahy o této rovnici sepsal už Ptolemaios ve 2. století n. l., v době, kdy hodiny pro přesnější srovnání ještě neexistovaly.

Různé časové soustavy, ale stejný čas

Rovnice E = T_P – T_S, včetně variant pro E₁ a E₂, je rovnice popisující stejný časový okamžik (čas t) a znamená rovnici E (t) = T_P (t) – T_S (t). Hodnoty T_P, T_S1, T_S2 jsou jen různé časové souřadnice pro stejný okamžik t, nejsou to různé fyzikální časy. Jsou to „časy“ na různých „hodinkách“. Souřadné soustavy pro čas t jsou zde tři: pravý čas, 1. střední čas a 2. střední čas. Ani jeden z těchto „časů“, dokonce ani T_S není absolutně totožný s časovou souřadnicí měřenou například jako „atomový čas“.

1.5 Dvě složky rovnice času

E = E₁ + E₂, kde
E₁ = T_P – T_S1, tj. časový rozdíl mezi pravým (S_P) a 1. středním Sluncem (S₁)
E₂ = T_S1 – T_S2, tj. časový rozdíl mezi 1. (S₁) a 2. středním Sluncem (S₂)

Potom platí, že E = E₁ + E₂ = T_P – T_S2 = T_P – T_S, kde E je rozdíl mezi pravým a středním (=2. středním Sluncem)

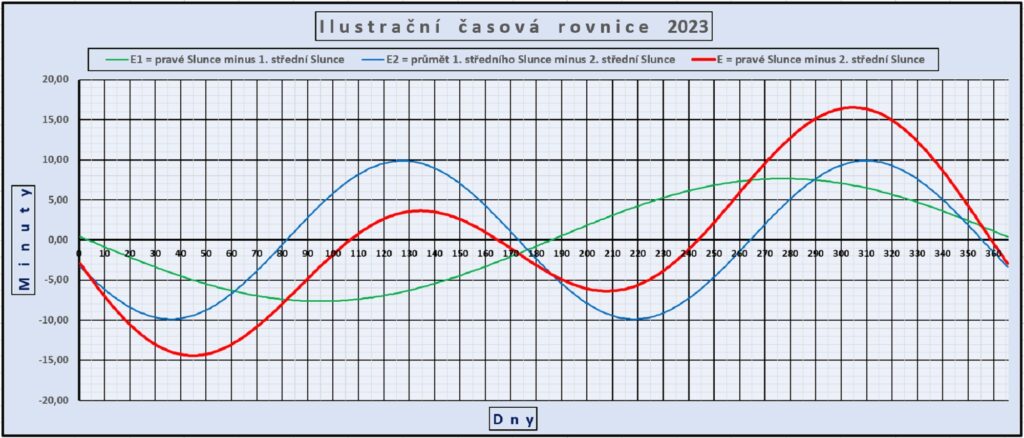
Proč tu vůbec nějaké střední Slunce je? Rotace Země funguje jako oscilátor taktující poměrně stabilní časové jednotky, setrvačníkové „hvězdné“ dny, ale změny polohy Země na elipse, resp. Slunce na kružnici v případě ekliptiky, do toho vnáší kromě proti-otáčení jako přidaného úhlu také nerovnoměrný pohyb. Rychlost proti-otáčení kvůli Keplerovým zákonům není stabilní. Proto vzniká rozdíl mezi střední a reálnou rychlostí, mezi středním a skutečným úhlem, pod kterým vidíme Slunce. Jinak by rychlost byla jen jedna (pokud by navíc byla osa rotace Země k rovině ekliptiky kolmá).

Pokud je osa Země skloněná, je zdrojem další nerovnoměrnosti. Pohyb S₁ i S_P se promítá do pohybu na rovníkové kružnici a nemění se jen poloha, ale také rychlost. Střední Slunce S₁ promítnuté do roviny rovníku, kde ho označíme jako S_1P už není žádné střední Slunce, S_1P mění rychlost svého pohybu a musí se opětovně středovat na S₂. Slunce S_1P se pohybuje po kružnici rovníku ve stejném okamžiku (synchronizovaně) jako S₁ po kružnici ekliptiky. Platí to i pro S_P a jeho průmět.

E₁ = (T_P – T_S1)_{na ekliptice} = (T_Pprůmět – T_S1průmět)_{na rovníku}
E₂ = (T_S1 – T_S2)_{na rovníku}  = (T_S1průmět  – T_S2)_{na rovníku}
E = (E₁ + E₂)_{na rovníku} = (T_Pprůmět – T_S2)_{na rovníku} = (T_P – T_S2)   

2. První střední Slunce a funkce E₁

2.1 Graf a data pro funkci E₁

Země se pohybuje po elipse a Slunce není ve středu elipsy, ale v jednom z jejich ohnisek. Zeměkoule se pohybuje nerovnoměrně, dle Keplerových zákonů, někdy rychleji a jindy pomaleji. Vzhledem k tomu, že nemůžeme pozorovat sami sebe, pozorujeme pohyb Slunce na nebi a skutečný pohyb Země je vnímán jako denní a roční „zdánlivý“ pohyb Slunce.

Důsledkem nerovnoměrného pohybu Země kolem Slunce je nerovnoměrný pohyb Slunce na nebeské sféře.

Promítáním pohybu Slunce na nebeskou sféru dochází k „záměně“ pohybu dvou nebeských těles. Z hlediska pozorovatele na Zemi se na nebeské sféře pohybuje Slunce a obíhá Zemi po ekliptice, tj. kružnici, jejíž „vzorem“ je ve skutečnosti eliptická dráha Země kolem Slunce.  

První střední Slunce je virtuální neexistující objekt, který se pohybuje rovnoměrně. Nepohybuje se po elipse, ale po kružnici. Se skutečným pravým Sluncem se 1. střední Slunce setká na „oběžné dráze“ 2x, v perihéliu a v aféliu (přesněji v průmětech těchto bodů na nebeské sféře). Pohyb 1. středního Slunce kolem Země nahrazuje pohyb fiktivní střední Země, pohybující se průměrnou rychlostí po kružnici, v jejímž středu by bylo Slunce.   

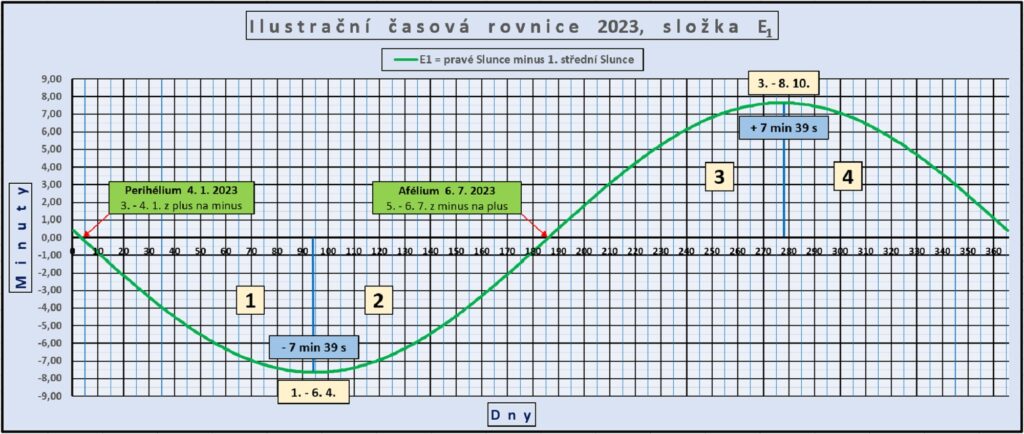
Data ke grafu

Nulovou hodnotou z plus na minus prochází křivka ve dnech 3. – 4. ledna (dny 3 a 4), a pak z minus na plus 5. – 6. července (dny 186 a 187), protože perihélium nastává 4. 1. 2023 a afélium 6. 7. 2023.

Maximální záporné odchylky -7 min 39 s křivka dosahuje ve dnech 1. 4. (91. den) – 6. 4. (96. den).
Maximální kladnou hodnotu +7 min 39 s křivka dosahuje 3. 10. (276. den) – 8. 10. (281. den).

Zdroj astronomických dat pro hodnoty rovnice času:
https://kalendar.beda.cz/hodnoty-casove-rovnice

2.2 Obrázek pohybu Sluncí, který generuje časový rozdíl E₁

Účelem následujícího obrázku je zobrazit, jak je promítáno Slunce na nebeskou sféru při eliptickém oběhu Země kolem Slunce, které se nachází v jednom z ohnisek elipsy. Po promítnutí Slunce na nebeskou sféru můžeme dát do středu nebeské sféry Zemi. Ta při ročním oběhu kolem Slunce zároveň rotuje ve stejném směru kolem své osy. Vzhledem k vzdálenostem ve vesmíru je nebeská sféra prakticky nekonečně daleko ve srovnání se vzdáleností Země a Slunce.

Obrázek, spolu s předcházejícím grafem, ukazuje souvislost mezi rychlostí, polohou a časem, mapovaným geometrickým úhlem.

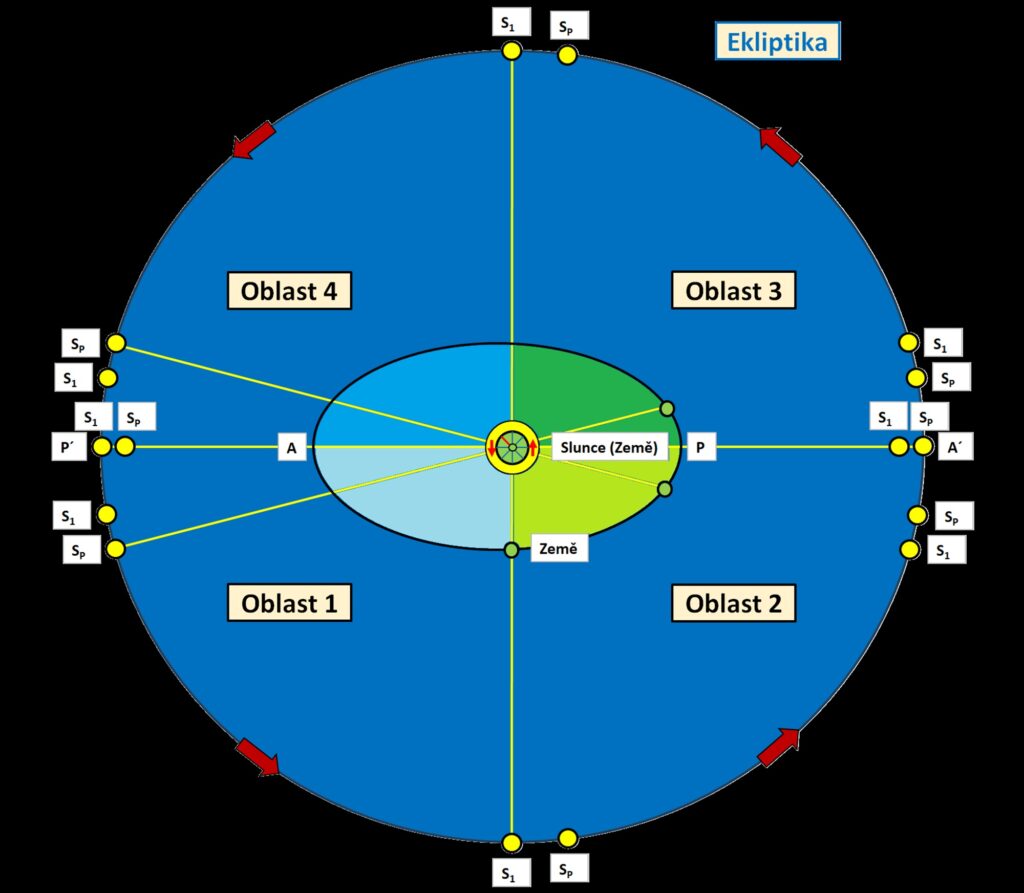
Popis značení na obrázku

S₁ – 1. střední Slunce, S_P – pravé Slunce,
P, A – perihélium a afélium,
P´, A´ – průmět perihélia a afélia na ekliptiku.

2.3 Komentář k obrázku pohybu Sluncí a složce E₁ rovnice času

Někdo by si mohl myslet, že když je na ekliptice pravé Slunce před středním, viz předchozí obrázek, tak nad hlavou budeme mít nejdříve pravé poledne a až pak střední. Zní to logicky, ale je to naopak.

Střední poledne předběhne pravé. Proč? Protože my nepozorujeme Slunce z nějakého „nehybného matematického bodu“ (to by neexistoval den), ale z povrchu rotující Země. Otáčení zeměkoule má stejný směr jako její pohyb po oběžné dráze (na ekliptice ho nahrazuje Slunce), jen je 365x rychlejší. Země se točí na východ, takže hvězdy na nebi se pohybují na západ, opačným směrem. Čím víc je pravé Slunce na ekliptice před středním, tím více se Země musí v rámci jednoho dne k poledni „dotočit“.

Z hlediska pozorovatele kulminace Slunce na Zemi nastane poledne dříve u toho Slunce, které se objeví jako první v rovině rotujícího meridiánu. Na obrázku je zobrazen červeně a točí se proti směru hodinových ručiček. Na nebi se proto „hvězdy“ objevují v opačném pořadí, než je pořadí při jejich ročním pohybu po ekliptice. Platí to i pro pravé a střední Slunce. Úhly, definující polohy Sluncí na ekliptice (viz obrázek) a pro pozorovatele na Zemi jsou velikostí stejné, ale opačně orientované.

(α_P – α_S1)_{na rotující Zemi} = – (α_P – α_S1)_{úhel na ekliptice, Země jako bod}

Další text a většina úvah vychází z orientace úhlů na ekliptice, viz obrázek vzájemného pohybu Sluncí.

Oblast 1 – od začátku křivky po minimum

V perihéliu se střední Slunce potkává s pravým (E₁ = 0). Protože v perihéliu je rychlost Země a pravého Slunce větší než průměrná, pravé Slunce předběhne virtuální střední, a proto je potřebné k otočení Země do středního poledne přidat ještě další „dotočení“ k tomu pravému. Delší dráha pravého Slunce na nebi znamená větší „dotáčení“ zeměkoule. V oblasti 1 pravé Slunce, jako obraz pohybu Země po elipse (pozorovaný jako pohyb Slunce po ekliptice), uniká stále víc virtuálnímu „střednímu“ Slunci, a vzdaluje se mu přesto, že jeho rychlost cestou do afélia postupně klesá. Platí: E₁ (= T_P – T_S1) < 0. „Pravé poledne“ v oblasti 1 zaostává za středním (uvažujeme jen o složce E₁).

Oblast 2 – od minima křivky po nulový bod

Pravé Slunce v perihéliu sice předběhne střední, ale jeho rychlost se v oblasti 1 trvale zpomaluje. Rozdíl mezi pravým a středním časem trvale narůstá, ale vzhledem ke zpomalování pravého Slunce se přírůstek stále zmenšuje. V bodě minima křivky (začátek oblasti 2) se přírůstek zastaví úplně. Je to způsobeno tím, že se rychlost pravého Slunce zmenší na rychlost středního a vzdálenost mezi nimi se už dál nezvětšuje. Pravé Slunce se bude do afélia i nadále zpomalovat, a proto rychlost středního Slunce bude už větší než rychlost pravého. Časový rozdíl a vzdálenost mezi nimi se bude zmenšovat, až se v aféliu setkají. V oblasti 2 stále platí E₁ < 0. „Pravé poledne“ zaostává za středním (jen složka E₁).

Oblast 3 – od nulového bodu křivky po maximum

Aféliem (E₁ = 0) prochází už pomalé pravé Slunce, a proto ho střední předběhne a začne se mu stále víc vzdalovat. Rozdíl mezi pravým a středním časem trvale narůstá. Nakonec vzdálenost mezi nimi dosáhne maxima a tomuto maximu bude odpovídat i maximální rozdíl E₁ mezi příslušnými časy na konci oblasti 3. Zaostávání pravého Slunce za středním znamená, že se otočení Země do pravého poledne uskuteční dříve než do středního. V oblasti 3 platí E₁ > 0. „Pravé poledne“ předchází střednímu (jen složka E₁).

Oblast 4 – od maxima křivky až na konec periody

V okamžiku maxima křivky pro rozdíl časů E₁ rychlost pravého Slunce dosáhne rychlosti středního. Jejich vzájemná vzdálenost a rozdíl mezi pravým a středním časem přestane narůstat. Vzhledem k nadále rostoucí rychlosti pravého Slunce se začne vzdálenost Sluncí i rozdíl mezi pravým a středním časem zmenšovat, protože se Slunce k sobě přibližují. Hodnota E₁ > 0 platí i nadále. Nakonec se střední a pravé Slunce setkají v novém perihéliu, kde E₁ = 0. „Pravé poledne“ v oblasti 4 předchází střednímu (jen složka E₁).

Pozn.: „Pravé poledne“ je tu pomocný pojem vztažený jen na první část pohybu, složku E₁.

2.4 Rychlosti pohybu Sluncí

Rychlost Země, resp. promítaného pravého Slunce, je maximální v perihéliu, ale na křivce E₁ tam vidíme nulový bod a lokální extrém je posunutý. Proč není největší časový rozdíl tam, kde je největší rychlost, tj. v perihéliu? Jaký je vztah mezi rychlostí a polohou?

Průběh rychlostí reprezentuje derivace křivky sinus, derivace rovnice E₁ = T_P – T_S1 = (α_P – α_S1)_{na rotující Zemi}, kde cosinus nabývá maxima v perihéliu a minima v aféliu. Ale odkdy je derivace času rychlost? Tak obecně to určitě neplatí, ale tady je čas E₁ mapovaný na základě pohybu Sluncí. Měří se úhel alfa, pod kterým Slunce pozorujeme na nebi a úhlová rychlost je přes poloměr svázaná s obvodovou rychlostí. Úhel a čas jsou zde stejné navzájem rovné veličiny. Obvodové rychlosti jsou úměrné (~) času a správnou konstantou je možné nastavit i jejich rovnost.

Pravý čas je mapovaný jako α_P, střední čas jako α_S1, potom E₁ = – (α_P – α_S1)_{na ekliptice, bodová Země}. Čas E₁ uplyne po otočení Země z jednoho úhlu do druhého. Zkoumáním změn v čase, tj. derivací (spojitou nebo diskrétní, celkovou změnou za den), získáme průběh relativní úhlové rychlosti ω_r = (ω_P – ω_S1) nebo relativní obvodové rychlosti v_r = (v_P – v_S1). Úhel α na ekliptice je kladný proti směru hodinových ručiček v geometrii, kde Země je jen bodový střed ekliptiky jako kružnice.

–dE₁/dt = (dα_P/dt – dα_S1/dt) = (ω_P – ω_S1) = ω_r = v_r/r = (v_P – v_S1)/r

v_r = konst₁ * dE₁/dt, ω_r = konst₂ * dE₁/dt

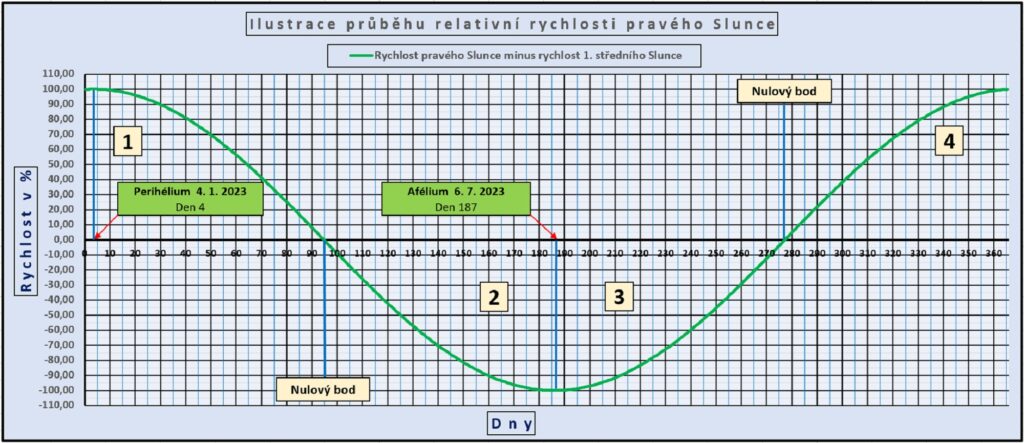
Relativní úhlová rychlost ω_r nebo obvodová rychlost v_r je úměrná -(d/dt) E₁, kde r je poloměr kružnice nahrazující elipsu (v_S1 = ω_strední * r).

Pokud (d/dt) E₁ = 0, tak (v_p – v_S1) = 0, vzájemná relativní rychlost Sluncí je nulová a jejich vzdálenost se nemění (proto se nemění E₁).

Průměrná rychlost pohybu pravého Slunce je někde mezi maximální a minimální rychlostí, při symetrii v polovině. Obě Slunce se setkají v bodě perihélia, tam bude křivka rozdílu časů E₁ začínat nulou a 1. lokální extrém (minimum) bude v polovině mezi perihéliem a aféliem. Viz dřívější komentář pro oblast 1 a 2. Další nulový bod bude v aféliu, po něm bude následovat maximum atd.

Na úvodní otázku: Proč není největší časový rozdíl tam, kde je největší rychlost, je poměrně rozsáhlá a podrobná odpověď v kapitole 2.6. Jak bude uvedeno o kousek dál, pohyby mají v průmětu charakter kmitů, což ukazuje i tzv. analema, takže i průběh pohybů a rychlostí bude podobný.

2.5 Proč by právě sinus mohl modelovat průběh funkcí E₁ a E₂

Kde se tu vzal sinus? Z čeho plyne, že průběh funkce by měla popisovat právě tato funkce? A proč tam vůbec jsou goniometrické funkce? Když se ve fyzice řeší nějaký problém, sestavují se rovnice na základě fyzikálních zákonů a z nich potom plyne řešení v podobě výsledných matematických funkcí. Takové exaktní řešení hledá i astronomie, tady to ale chceme udělat jinak, intuitivně, s minimem rovnic.

Víme jen to, že:
E₁ = T_P – T_S1 = (α_P – α_S1)_{na rotující Zemi} = – (α_P – α_S1)_{na ekliptice}

Nevíme, jaký tvar má funkce E₁ (t) ani jak se mění v čase. Pokud se podíváme na obrázek pohybu Sluncí, který generuje časový rozdíl E₁, zjistíme, že pravé Slunce se někdy překrývá se středním a α_P = α_S1. Někdy je hodnota (α_P – α_S1) kladná a někdy záporná. Obrázek ale vychází z už hotového grafu pro E₁ a tak by to byl logický kruh. Je třeba hledat dál.

Pokud má nějaká měnící se veličina (např. poloha nebo rychlost) průměr, tak musí být nějaké hodnoty nad a jiné hodnoty pod průměrem. Ten bude při výpočtu hodnot (+y a -y) ve středu odchylek na ose x. A pokud se tyto hodnoty mění v čase spojitě, ne skokově, musí se propojit spojitou křivkou reprezentující postupnou změnu. Hodnoty se navíc mění opakovaně, periodicky. Nejjednodušší propojení bodů nad a pod osou jsou funkce sinus nebo cosinus, to jsou dvě funkce prakticky totožné, jen fázově posunuté, takže to bude alespoň v 1. přiblížení nějaká goniometrická funkce.

Vztahy mezi znaménky E₁ a obvodovými rychlostmi na ekliptice

Relativní poloha Sluncí na ekliptice má opačné znaménko jako pozorování této polohy na rotující Zemi definující E₁.  Kladná relativní poloha S_P před S₁, (α_P – α_S1) > 0, na ekliptice znamená zápornou hodnotu E₁ a opačně.

Po derivaci se relativní poloha změní na relativní rychlost. Orientace všech úhlů α_P, α_S1, atd. je ve shodě s jejich orientací na ekliptice (dle obrázku „pohybu Sluncí“).

Pokud je číselná (skalární) relativní rychlost Sluncí (v_p – v_S1) > 0, tj. v_p > v _S1, rozdíl Δ E₁ je záporný, každá další hodnota je menší v kladných i záporných číslech. A pozor: jde o Δ, tj. změnu E₁, ne E₁, které je také rozdílem časů.

(v_p – v_S1) > 0, v_p > v_S1, oblasti 4 a 1, Slunce se nejdříve přibližují (S_P je za S₁), a po setkání vzdalují
(S_P je před S₁), Δ E₁ < 0 

(v_p – v _S1) < 0, v_p < v_S1, oblasti 2 a 3, Slunce se nejdříve přibližují (S_P je před S₁), a po setkání vzdalují
(S_P je za S₁), Δ E₁ > 0

2.6 Důležité charakteristiky pohybu Sluncí na hranicích oblastí

V bludišti poloh, vzájemných rychlostí a různých časů (přesněji časových souřadnic), nám může být při úvahách pomůckou nějaká analogie. Rovnice času popisuje „pomalé kmity“ časových souřadnic kolem nějaké střední hodnoty. Ve skutečnosti ale nekmitá nějaký záhadný čas, ale na obloze se promítají složité vzájemné pohyby nebeských těles do periodických pohybů. Podobný charakter má kyvadlo, i tady se něco pohybuje a kmitá kolem středu.

Pro amplitudy a rychlosti kyvadla platí:

1. kde je maximální amplituda, tam je rychlost tělesa nulová a mění svůj směr na opačný
2. kde je střed amplitud (výchylek na jednu i druhou stranu), tam je rychlost tělesa maximální

Pro 1. střední Slunce platí, že průběh rychlosti vůči nějaké střední rychlosti reprezentuje křivka cosinus začínající v perihéliu, tam je rychlost maximální, v aféliu je minimální.  Obě hodnoty jsou stejně vzdálené od střední hodnoty. Uprostřed mezi perihéliem a aféliem bude hodnota rychlosti pravého Slunce nulová. Kde je rychlost Země na oběžné dráze (resp. promítnutého Slunce) nulová? Nikde, ale tady hledáme nulu vůči střední rychlosti (tj. relativní rychlost), ne skutečně nulovou rychlost pohybu.

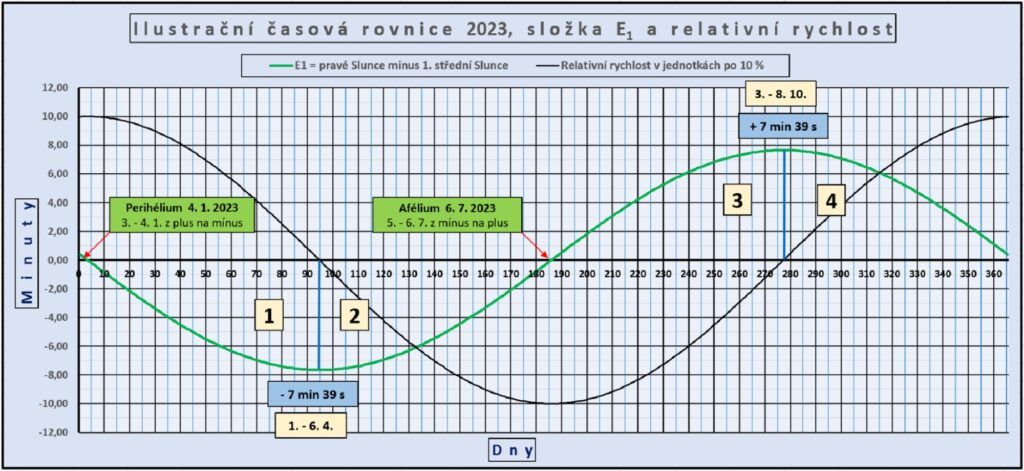
Střední rychlost je mezi maximální a minimální, nulová relativní rychlost bude z tohoto hlediska při symetrii uprostřed mezi perihéliem a aféliem. V tomto bodě se mění i směr této rychlosti jako vektor. Ne, že by se Země otočila a začala couvat, ale relativní rychlost se změní z kladné na zápornou (nebo opačně).

Opačný směr znamená, že vzdalování nebeských těles se změní na přibližování (viz obrázek, hranice oblasti 1 a 2) a opačně. Na obrázku se vychází z už stanovených poloh míst setkání Sluncí.

Obecně je ale pro rychlosti možné říci jen to, že v oblasti 1 a 4 je rychlost pravého Slunce větší než 1. středního a v oblasti 2 a 3 je rychlost S_P menší než rychlost S₁. Je to jako v autě, pokud výsledný vektor (velikost a směr) rychlostí dvou aut směřuje k druhému, auta se přibližují, pokud má opačný směr, tak se vzdalují. Větší rychlost pravého Slunce než středního, může znamenat někdy přibližování a jindy vzdalování. Vše závisí na výchozí poloze.

Maxima a minima jako hranice oblastí 1 a 2 nebo 3 a 4

Středy mezi perihéliem a aféliem (hranice oblastí 1 a 2 nebo 3 a 4) jsou body „lokálních“ amplitud Δt funkce E₁ (plusové a minusové), nulové relativní (vzájemné) rychlosti těles a zároveň obratu mezi přibližováním a vzdalováním pro tělesa S₁ a S_P obecně.

Na hranicích oblastí 1 a 2 nebo 3 a 4, definovaných lokálními extrémy E₁, se relativní rychlost (v_p – v_S1) mění na opačnou, z plus na minus nebo z minus na plus. Slunce se v obou případech až po hranici oblastí nejdříve vzdalují, a pak přibližují.

Lokální extrémy funkce sinus se neposouvají doprava ani doleva. Zůstávají tam, kde jsou i při všech myšlených (teoretických) posunech polohy S₁ na ekliptice vůči S_P. Mění se jen amplitudy. Proč? Průběh rychlostí je dán Keplerovými zákony, maximální rychlost je v perihéliu, minimální v aféliu. Mezi nimi je nulová relativní rychlost, a právě ta definuje polohu x maximální amplitudy y funkce E₁. Jen při nulové relativní rychlosti se může vzájemný pohyb otočit opačným směrem (přibližování na vzdalování a opačně). Při nenulové rychlosti by vzájemný pohyb pokračoval v původním směru dál.

Nulové body funkcí

Nulové body funkce E₁ jsou body setkání Sluncí. Při pohybu do tohoto bodu se Slunce navzájem přibližují a po průchodu nulovým bodem se vzdalují. Kde je nulový bod amplitudy E₁, nemůže být nulová rychlost, protože by se tam vzájemný pohyb zastavil a změnil směr, místo toho, aby pokračoval dál. Nulové body se za jistých okolností posouvat mohou a v jednom zvláštním případě tam při shodě s amplitudou může být i nulová vzájemná rychlost (viz kap. 2.7).

2.7 Fázově posunuté střední Slunce (myšlenkový experiment)

Co kdyby vystředovaný virtuální objekt obíhal stejnou rychlostí, ale úhlově (fázově) posunutý. Jen ze středování veličiny rychlosti nijak neplyne, kde konkrétně takové střední Slunce z hlediska polohy musí být. Víme jen, že musí mít nějakou průměrnou rychlost. Kde bude nová střední poloha?

Při pozorování průmětů pohybů Slunce na obloze je střední Slunce mezi krajními polohami těch pravých, protože i když je teoretické, reprezentuje vždy pohyb skutečného Slunce, a ne nějaký neznámý objekt na obloze. Tady otázka, kde by střed měl být ani nevznikne. Kde jinde než uprostřed krajních poloh. Přesto je otázka, co by se stalo při fázovém posunu středního Slunce, zajímavá.

Posun fáze středního Slunce

Pokud body setkání tvoří perihélium a afélium, a funkce E₁ pro amplitudu Δt je symetrická, suma všech kladných odchylek je stejná jako suma všech záporných. Střed je uprostřed odchylek. Pokud by bylo na oběžné dráze ještě jiné virtuální střední Slunce (definované jen střední rychlostí a fázově posunuté), ke každé dřívější časové odchylce by se musela přičítat ještě fixní hodnota úhlu (času) odpovídající rozdílu fáze mezi S₁ (původním středním Sluncem) a novým posunutým S_1posunuté.

Výsledek takového posunutí je na dalším grafu, kde je vidět, že posun fáze má zajímavé důsledky. Stačí úhel odpovídající času většímu než 7 min a 39 s a Slunce se nesetkají vůbec. Obě tělesa se mohou navzájem honit jako pejsek a kočička po lese, někdy se budou přibližovat, a jindy vzdalovat, ale nemusí se nikdy dohonit a navzájem předběhnout.

Posunutí S₁ na ekliptice reprezentuje posun grafu funkce E₁ svisle a vznik nových nulových bodů. Hranice oblastí se posouvají, ale symetrie zůstávají kolem maximálních amplitud. To zachovává základní logiku, že maximální výchylka z nulového bodu (místa setkání Sluncí) na jednu stranu trvá stejně dlouho jako návrat zpět do nulového bodu (následujícího místa setkání). Zajímavým důsledkem je, že samotné výchylky (amplitudy) z nulových bodů budou výrazně odlišné.

Body maximální vzájemné rychlosti (určené Keplerovými zákony) se nezmění, jsou na ose x uprostřed mezi lokálními extrémy E₁. Průběh rychlostí jako cosinus je zachován, derivace konstantu posunu funkce E₁ zruší.

Nulové body už nejsou uprostřed časového intervalu mezi amplitudami. Nulové body určujeme volbou (zda chceme, aby to „kmitalo“ opravdu kolem středu nebo jinde).

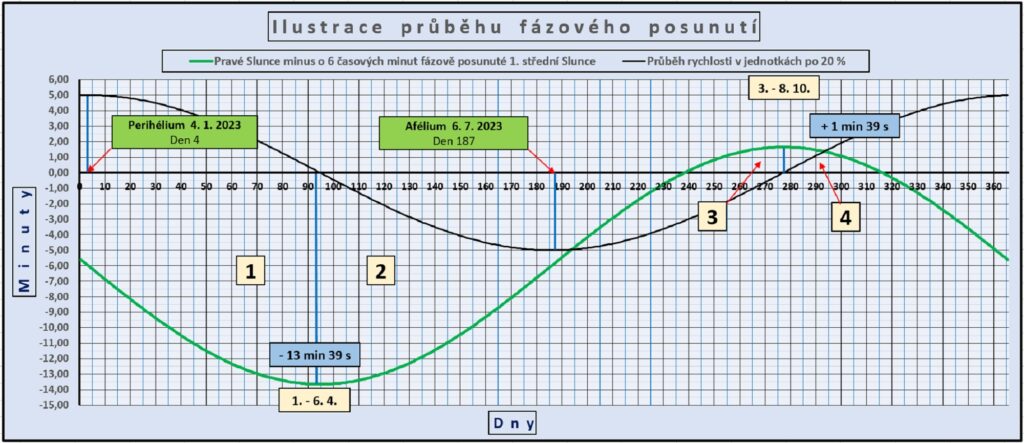
Kde všude může nastat setkání pravého a virtuálního středního Slunce?

1. v bodech perihélia a afélia (pokud střed volíme uprostřed výchylek, S₁ bez fázového posunutí)
2. v libovolných jiných bodech, symetrických kolem maxim a minim funkce E₁
3. jen v 1 bodě maxima nebo minima, nulový bod rychlosti se stává totožným s bodem amplitudy, možná, ale nepřirozená situace, kdy je „střed“ z nějakého důvodu nastaven na kraj amplitudy
4. v žádném bodě, k setkání Sluncí nedojde

Proč se pravé a střední Slunce setkávají právě v perihéliu a v aféliu?

Body setkání Sluncí nemohou být s výjimkou jednoho výše uvedeného případu v bodech nulové vzájemné rychlosti, protože by se tam vzájemný pohyb zastavil a změnil směr, místo toho, aby pokračoval dál. Musí v nich být nenulová rychlost. A pokud budou výchylky poloh reprezentované E₁ symetrické, suma kladných odchylek bude stejná jako suma záporných, nastaví se do maxima a minima rychlostí. Perihélium a afélium jako místo setkání Sluncí je určeno průběhem rychlostí a přirozenou volbou, aby součet odchylek od střední polohy byl nulový (víc o tzv. inflexních bodech je v kap. 3.6).

3. Druhé střední Slunce a funkce E₂

Nerovnoměrný pohyb pravého Slunce po ekliptice je příčinou nerovnoměrného zdánlivého proti-otáčení. Jeho průměrováním vzniká 1. střední Slunce. To se pohybuje rovnoměrně. Otázkou je, jak bude pohyb tohoto vystředovaného Slunce po ekliptice přispívat k proti-rotaci v jiné rovině, tj. jak se rovnoměrný pohyb po jedné kružnici promítne do nerovnoměrných změn rychlostí a poloh na druhé skloněné kružnici v rovině rotace Země, tj. na nebeský rovník.

Promítnutím 1. středního Slunce do roviny nebeského rovníku vznikne nový fiktivní objekt S_1P (promítnuté Slunce S₁). Analýza geometrie pohybu ukazuje, že se tento virtuální objekt pohybuje v prostoru opět nerovnoměrně.

Až vystředováním tohoto dalšího virtuálního objektu S_1P dostaneme 2. střední Slunce (S₂). Druhé střední Slunce je pojem, který už zohledňuje sklon zemské osy. Pokud chceme sečíst úhly, musíme je zkoumat ve společné rovině, tj. v rovině kolmé k ose rotace (chceme sečíst úhel proti-rotace s rotací). Proto se pohyb 1. středního Slunce po ekliptice musí nejdříve promítnout do roviny nebeského rovníku a tam zprůměrovat. Úhlům v rovině rotace přísluší mapované časy, které je potom možné sečíst.

S₂ se tedy pohybuje po kružnici nebeského rovníku rovnoměrně. Vzhledem ke kružnicím v prostoru se s pravým Sluncem může „reálně“ setkat jen v jarním a podzimním bodě. To jsou průsečíky ekliptiky a nebeského rovníku, tj. polohy Země (promítnutého Slunce) v době jarní a podzimní rovnodennosti.

Průběh funkce E₂ a vzájemný pohyb Sluncí je překvapující a velice zajímavý. Pohyb prvního středního Slunce vzhledem k pravému Slunci vede k sinusoidě s poměrně složitým průběhem poloh a vzájemných rychlostí. Pohyb druhého středního Slunce vzhledem k průmětu S₁ je ještě mnohem složitější a vede k 2x rychlejší změně fáze a k dvojnásobnému počtu maxim a minim. Ve své podstatě jednoduché pohyby nebeských těles komplikují vztahy vzájemných relativních rychlostí a poloh mezi pravým a středním Sluncem.

3.1 Promítání v prostoru a změna úhlu od 0⁰ do 23,5⁰

Pokud funkci E₁ určují Keplerovy zákony (pohyb po elipse, body jako perihélium a afélium), funkci E₂ určuje geometrie, sklon mezi rovinami nebeského rovníku a ekliptiky. Úhel mezi rovinami je konstantní, ale úhel mezi křivkami v těchto rovinách, tj. dráhami těles, se spojitě mění. Důležitou roli v této geometrii hrají limitní body, hranice měnícího se úhlu. Jsou to dny slunovratů a dny rovnodennosti, kde dochází k podstatné změně úhlu mezi ekliptikou a nebeským rovníkem.  

1. střední Slunce se pohybuje po kružnici – ekliptice rovnoměrnou střední rychlostí. Tuto rychlost je potřebné promítnout prostorově do roviny nebeského rovníku, aby se mohl započítat vliv 1. středního Slunce (S₁) k rotaci kolem osy Země. Podle obrázku je vidět, že „v bodech“ zimního slunovratu a letního slunovratu jde o nad sebou umístěné rovnoběžky a průmět rychlosti Slunce S₁ do roviny rovníku bude zachován a nezmenšen, promítne se kolmicí na rovník jako složka vektoru rychlosti.

Dál se úhel mění spojitě až do trojúhelníků s jarním a podzimním bodem. V bodech jarní a podzimní rovnodennosti je to „limitní trojúhelník“, kde proměnný úhel naráží na hranici danou úhlem obou rovin. Průmět rychlosti 1. středního Slunce do roviny rovníku se zmenšuje jako cos α. Pro jarní a podzimní rovnodennost je to v limitě úhel 23,5⁰, směrem k letnímu a podzimnímu slunovratu se úhel spojitě mění. Pro slunovraty je α = 0⁰ a cos α = 1, průmět vektoru rychlosti je nezmenšený.

Trojúhelník promítání pohybu v bodech jarní a podzimní rovnodennosti

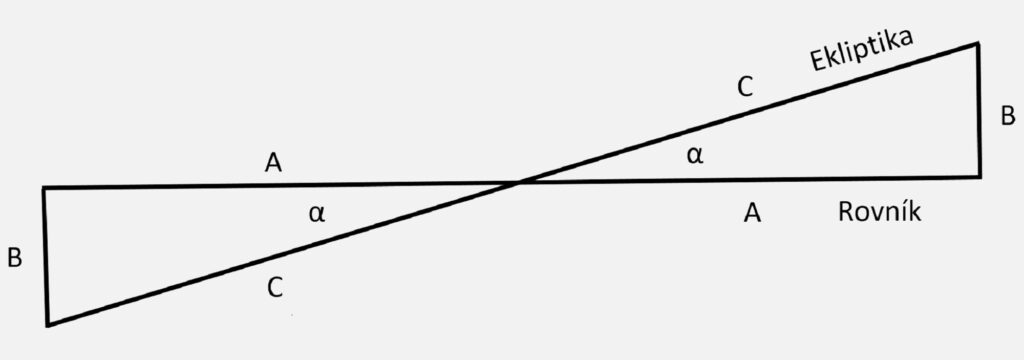
A/C = cos α

Úhel α při pohybu v prostoru není fixní. Za skutečnost, že se z rovnoměrné rychlosti 1. středního Slunce stane nerovnoměrný pohyb, může měnící se úhel α a jeho cosinus (A = C*cos α). Zatímco křivka 1. středního Slunce měla jedno maximum a jedno minimum, tady budou 2 maxima a 2 minima a rychlost průběhu fáze funkce cosinus se zdvojnásobí.

Ve dnech zimního a letního slunovratu je rychlost průmětu 1. středního Slunce (v_S1p) maximální a ve dnech jarní a podzimní rovnodennosti je minimální. Tato rychlost se ale neanalyzuje jako samostatná, ale jako relativní rychlost vztažená k nějaké střední hodnotě. To má za následek, že se z minimální rychlosti stane druhá „maximální“ rychlost, lišící se od první jen zápornou hodnotou. Navíc se zkoumá rychlost a poloha vůči virtuálnímu objektu, pohybujícímu se střední rychlostí.

Vztah mezi okamžitou rychlostí a střední rychlostí byl rozebrán podrobně už u funkce E₁, pro funkci E₂ je to stejné, resp. podobné. Maximální a minimální relativní rychlost „kmitá“ kolem střední nulové hodnoty.

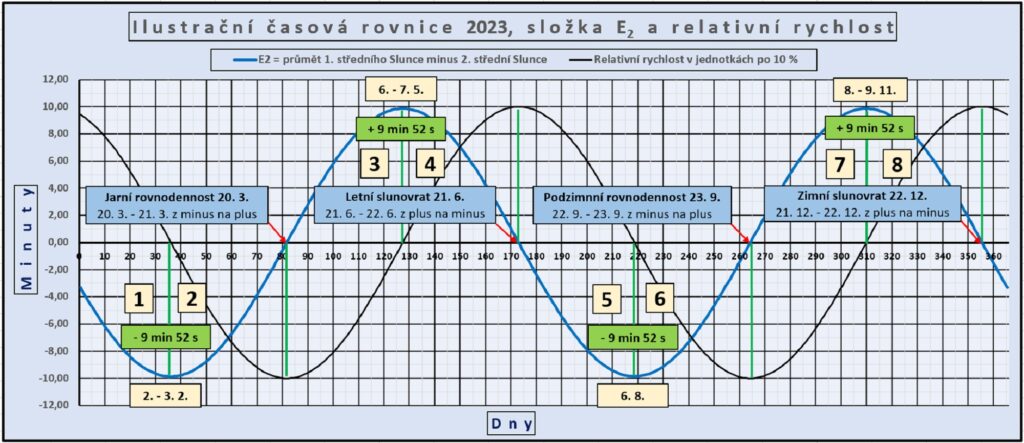
3.2 Graf a data pro funkci E₂

Nulovou hodnotou z minus na plus prochází křivka ve dnech 20. – 21. 3. (ve dnech 79 a 80), z plus na minus 21. – 22. 6. (ve dnech 172 a 173), z minus na plus 22. – 23. 9. (ve dnech 265 a 266) a z plus na minus ve dnech 21. – 22. 12. (ve dnech 355 a 356).

Zápornou hodnotu (– 9 min 52 s) křivka dosahuje 2. – 3. února (ve dnech 33 a 34), hodnotu + 9 min 52 s 6. – 7. května (ve dnech 126 a 127), hodnotu (– 9 min 52 s) 6. srpna (218. den) a hodnotu + 9 min 52 s 8. – 9. listopadu (ve dnech 312 a 313).

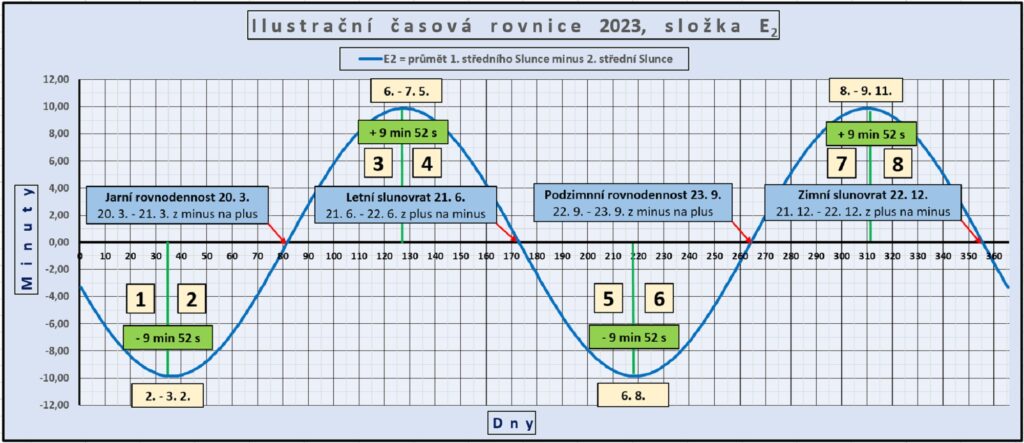
Výsledný tvar funkce E₂, a také tvar následné součtové funkce E, která ukazuje rozdíl „časových“ souřadnic (T_P – T_S), měřených na základě pohybu skutečného S_P a S₂, by čekal jen málokdo. Nečekaný je zejména dvojnásobný počet maxim a minim i poloha nulových bodů a lokálních extrémů.

3.3 Obrázek pohybu Sluncí, který generuje časový rozdíl E₂

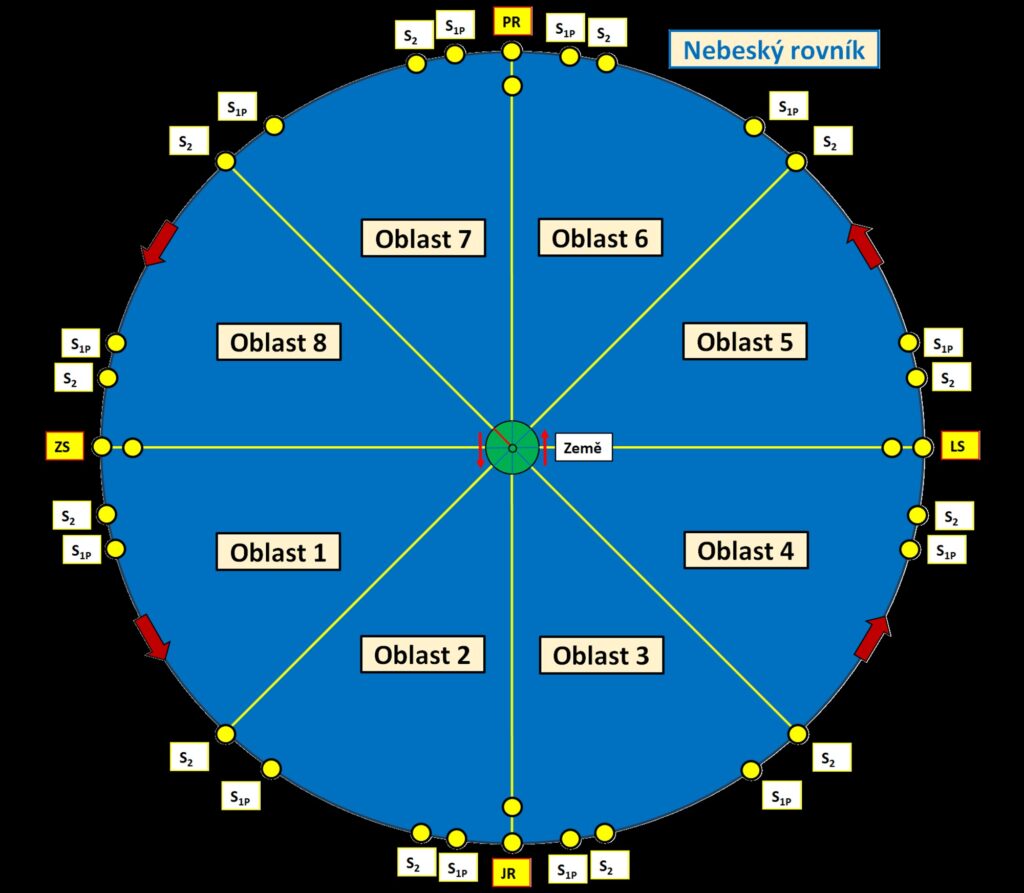
Popis značení na obrázku

ZS, LS – zimní a letní slunovrat,
JR, PR – jarní a podzimní rovnodennost,
S₁, S₂ – první a druhé střední Slunce, v_S1, v_S2 – rychlosti S₁, S₂,
S_1P – průmět 1. středního Slunce do roviny nebeského rovníku, v_S1P – rychlost S_1P.

Obrázek zobrazuje vzájemné polohy 2. středního Slunce a průmětu 1. středního Slunce z roviny ekliptiky do roviny nebeského rovníku. Jedná se o pomalý roční pohyb těles. Polohy jsou samozřejmě ilustrační a nezobrazují skutečné (úhlově přesné) vzdálenosti těles. Úhel 15⁰ na obloze odpovídá 1 hodině, takže 10 minut (maximální odchylka E₂) je 2,5⁰. Další reálné úhly jsou ještě mnohem menší. Na hranicích jednotlivých oblastí obrázek ilustruje principiální limitní polohy Sluncí a v mezi-polohách ukazuje pořadí Sluncí a velikost jejich vzdálenosti ve vztahu ke krajním polohám na hranicích oblastí.

Pozorovatel na Zemi rotuje daleko rychleji (365x) a má vzhledem ke shodnému směru rotace Země vzájemné polohy Sluncí prohozené. Dříve proto nastává ten „čas“, který je blíž k meridiánu.

3.4 Komentář k obrázku pohybu Sluncí a složce E₂ rovnice času

Oblasti 1 a 2

Vycházíme z bodu zimního slunovratu, kde se S_1P setká s S₂. ZS je bod, ve kterém je rychlost v_S1P maximální (viz cos α = 1), větší než v_S2.  S_1P je proto v oblasti 1 rychlejší a S₂ hned za ZS předběhne. Vzdálenost mezi Slunci narůstá, ale v_S1P se postupně zmenšuje a v jistém okamžiku se rychlosti vyrovnají. Na grafu je to bod minima křivky a na obrázku začátek oblasti 2.

Vzdálenost mezi Slunci se přestane zvětšovat a v oblasti 2 po průchodu minimem křivky začne klesat, protože v_S1P bude už menší než v_S2. Klesající rychlost v_S1P je spojena se zmenšujícím se E₂ v oblasti 2. Slunce se navzájem přibližují, časový rozdíl klesá a v bodě JR se obě Slunce znovu setkají.

V oblasti 1 a 2 je S_1P před S₂, ale z důvodu rychlé rotace Země vůči ročnímu pohybu bude v meridiánu pozorovatele na Zemi nejdříve S₂ a až poté S_1P. Vztah E₂ = T_S1 – T_S2 bude záporný, E₂ < 0.

Oblasti 3 a 4

Vycházíme z bodu jarní rovnodennosti, kde se S_1P setká s S₂. JR je bod, ve kterém je rychlost v_S1P minimální (viz cos 23,5⁰), menší než v_S2. S_1P je v oblasti 3 pomalejší, proto S₂ hned za JR předběhne S_1P. Vzdálenost mezi Slunci narůstá, ale rychlost v_S1P se postupně zvětšuje a v jistém okamžiku se rychlosti obou Sluncí vyrovnají. Na grafu je to bod maxima křivky a na obrázku začátek oblasti 4.

Vzdálenost mezi Slunci se přestane zvětšovat a v oblasti 4 po průchodu maximem křivky začne klesat, protože rychlost v_S1P bude už větší než v_S2. Rostoucí rychlost Slunce S_1P je spojena se zmenšujícím se E₂ v oblasti 4. Slunce se navzájem přibližují, časový rozdíl klesá a v bodě LS se obě Slunce opět setkají.

V oblasti 3 a 4 je S₂ před S_1P, ale z důvodu rychlé rotace Země vůči ročnímu pohybu bude v meridiánu pozorovatele na Zemi nejdříve S_1P a až poté S₂. Vztah E₂ = T_S1 – T_S2 bude kladný, E₂ > 0.

Oblasti 5 a 6

Vycházíme z bodu letního slunovratu, kde se S_1P setká s S₂. LS je bod, ve kterém je rychlost v_S1P maximální (viz cos α = 1), větší než v_S2. S_1P je v oblasti 5 rychlejší a S₂ hned za LS předběhne. Vzdálenost mezi Slunci narůstá, ale v_S1P se postupně zmenšuje a v jistém okamžiku se rychlosti vyrovnají. Na grafu je to bod minima křivky a na obrázku začátek oblasti 6.

Vzdálenost mezi Slunci se přestane zvětšovat a v oblasti 6 po průchodu minimem křivky začne klesat, protože rychlost v_S1P bude menší než v_S2. Klesající rychlost v_S1P je spojena se zmenšujícím se E₂ v oblasti 6. Slunce se navzájem přibližují, časový rozdíl klesá a v bodě JR se obě Slunce opět setkají.

V oblasti 5 a 6 je S_1P před S₂, ale z důvodu rychlé rotace Země vůči ročnímu pohybu bude v meridiánu pozorovatele na Zemi nejdříve S₂ a až poté S_1P. Vztah E₂ = T_S1 – T_S2 bude záporný, E₂ < 0.

Oblasti 7 a 8

Vycházíme z bodu podzimní rovnodennosti, kde se S_1P setká s S₂. PR je bod, ve kterém je rychlost v_S1P minimální (viz cos 23,5⁰), menší než v_S2. S_1P je v oblasti 7 pomalejší, proto S₂ hned za PR předběhne S_1P. Vzdálenost mezi Slunci narůstá, ale v_S1P se postupně zvětšuje a v jistém okamžiku se rychlosti obou Sluncí vyrovnají. Na grafu je to bod maxima křivky a na obrázku začátek oblasti 8.

Vzdálenost mezi Slunci se přestane zvětšovat a v oblasti 8 po průchodu maximem křivky začne klesat, protože rychlost v_S1P bude už větší než v_S2. Rostoucí rychlost S_1P je spojena se zmenšujícím se E₂ v oblasti 8. Slunce se navzájem přibližují, časový rozdíl klesá a v bodě ZS se obě Slunce opět setkají.

V oblasti 7 a 8 je S₂ před S_1P, ale z důvodu rychlé rotace Země vůči ročnímu pohybu bude v meridiánu pozorovatele na Zemi nejdříve S_1P a až poté S₂. Vztah E₂ = T_S1 – T_S2 bude kladný, E₂ > 0.

3.5 Vzájemné relativní rychlosti Sluncí

Vzájemné relativní rychlosti dvou Sluncí jsou definované u E₁ polohou perihélia a afélia (Keplerovými zákony) a u E₂ body slunovratů a rovnodenností (geometrií rovin ekliptiky a nebeského rovníku). Ke kontaktu dvou Sluncí (S_1P a S₂) dochází ve 4 bodech. V těchto bodech funkce E₂ prochází nulou.

Střední obvodová (úhlová) rychlost v_S1 oběhu Slunce S₁ po ekliptice je stejná jako obvodová (úhlová) rychlost v_S2 Slunce S₂ po nebeském rovníku (v_S1 = v_S2), protože průmět Slunce S_1P oběhne rovníkovou kružnici za stejný čas jako jeho vzor ekliptiku a poloměr kružnice r_S1 = r_S2. Střední rychlosti jsou stejné, ale příslušné virtuální objekty S₁ a S₂ jsou fázově posunuté, a o to jde.

Maximální rychlost v_S1p je v bodech letních a zimních slunovratů, minimální v bodech jarních a podzimních rovnodenností. Po vystředování je maximum a minimum relativní rychlosti (v_S1p – v_S2) stejně velké, jen má opačné znaménko.

(v_S1p – v _S2)/r = -(d/dt) E₂, kde E₂ je rozdíl časů, derivace je tu změna tohoto rozdílu, ne rozdíl sám. Pokud je rychlost derivace, platí i opak, že E₁ a E₂ je součet, integrál.

Pokud (v_S1p – v_S2) > 0, v_S1p > v _S2, oblasti 8, 1 a 4, 5, Slunce se nejdříve přibližují (S_1P je za S₂), a po setkání vzdalují (S_1P je před S₂), ΔE₂ < 0.

Pokud (v_S1p – v _S2) < 0, v_S1p < v _S2, oblasti 2, 3 a 6, 7, Slunce se nejdříve přibližují (S_1P je před S₂), a po setkání vzdalují (S_1P je za S₂), ΔE₂ > 0.

Čím víc je pravé Slunce na ekliptice před středním (a rozdíl poloh je stále kladnější), tím víc se pravé poledne na nebi opožďuje (rozdíl E₂ je stále zápornější).

Pokud (d/dt) E₂ = 0, E₂ se nemění, tak (v_S1p – v_S2) = 0, znamená to, že vzájemná relativní rychlost Sluncí je nulová a jejich vzdálenost se nemění (proto se nemění E₂).

3.6 Nulové body funkce E₂

Zvykne se uvádět, že 1. a 2. střední Slunce se setkávají v bodech JR a PR. Nebeský rovník a ekliptika jsou kružnice v prostoru, které se protínají jen v těchto bodech a z tohoto hlediska se ani nikde jinde Slunce setkat nemohou. Při pohledu na graf funkce E₁ ale vidíme, že nulové body jsou čtyři, ne dva.

Je to způsobeno tím, že graf popisuje rovinu nebeského rovníku, tj. průmět Slunce S₁ z roviny ekliptiky do roviny rovníku. Jak ukazuje nejen graf, ale i obrázek, v rovině nebeského rovníku dochází ke čtyřem setkáním Sluncí.

Proč se u E₂ Slunce setkávají právě v bodech ZS, JR, LS a PR?

Relativní rychlost je rovna nule jen v bodech lokálních extrémů E₂, uprostřed intervalů (ZS až JR), (JR až LS), (LS až PR), (PR až ZS). V těchto bodech dochází ke změně znaménka relativní rychlosti (proto je tam lokální extrém E₂, vzdalování se mění na přibližování a opačně).

Body setkání Sluncí nemohou být v bodech nulové relativní rychlosti, protože by se tam vzájemný pohyb zastavil a změnil směr, místo toho, aby pokračoval dál. Musí v nich být nenulová rychlost.

Pokud jsou výchylky poloh reprezentované lokálními extrémy E₁ symetrické kolem nuly, suma kladných odchylek bude stejná jako suma záporných. Maximální a minimální rychlosti jsou v tzv. inflexních bodech, kde má 1. derivace lokální extrém. Tyto body je možné očekávat mezi nejbližším maximem a minimem. U funkce sinus nastavené symetricky kolem osy x, budou nulové body a inflexní body E₁ totožné. Nulové body E₁ se tak nastaví se do maxim a minim rychlostí, tj do bodů ZS, JR, LS a PR.

Tyto body jako místa setkání Sluncí jsou určené průběhem rychlostí (geometrií rovin), symetrií funkce sinus a přirozenou volbou, aby součet odchylek E₂ od střední hodnoty byl nulový. Podobně jako u funkce E₁, by i zde bylo možné teoreticky (myšlenkově) střední Slunce S₂ fázově posouvat tak, aby se Slunce setkala v úplně jiných nulových bodech, nebo se nesetkala vůbec. Nulové body by pak byly posunuté a neshodovali by se s body ZS, JR, LS a PR. Extrémy rychlostí jako derivace by ale zůstaly v inflexních bodech, uprostřed mezi extrémy E₂.

3.7 Intuitivní konstrukce funkcí E₁, E₂ a E pro rovnice času

Podkapitoly o funkcích E₁ a E₂ ukončí souhrnná myšlenková konstrukce funkcí E₁ a E₂. Následující úvahy nemohou nahradit exaktní řešení astronomických rovnic, ale ukazují princip chování Sluncí na obloze a vzájemné vztahy mezi veličinami polohy, rychlosti a času. Na přesnější grafické zobrazení průběhu funkcí bylo nutné ilustrační průběhy funkcí napasovat na tabulkové hodnoty z astronomických měření. Žádné úvahy nemohou nikdy nahradit experimentální měření.

Konstrukce funkce E₁

Země obíhá kolem Slunce a na základě Keplerových zákonů se pohybuje nejrychleji v perihéliu a nejpomaleji v aféliu. Pohyby Země se promítají do zdánlivých pohybů pravého Slunce na obloze. Protože hledáme vztah mezi pravým a středním časem, úhlové a obvodové rychlosti pravého Slunce zkoumáme vůči nějaké střední rychlosti virtuálního středního Slunce, tj. jako relativní vzájemné rychlosti. Pak je maximum této nové veličiny v perihéliu stejně vzdálené od střední rychlosti jako minimum v aféliu. Lokální extrémy jsou stejně velké a rozdíl mezi nimi je pouze ve znaménku.

Pokud spojíme počátek funkce s perihéliem na začátku kalendářního roku, nejjednodušší spojitá funkce, která projde z maxima rychlostí v perihéliu přes nulovou relativní rychlost až do minima v aféliu je cosinus (ω (t) = k*cos (t)), což je jen fázově posunutý sinus. Ten potom pokračuje z minima v aféliu do nového maxima v dalším perihéliu atd.

Suma (integrál) ze součtu součinů relativní úhlové rychlosti (ω_P – ω_S1) krát dt (časový interval) dá celkový relativní úhel Δα_1rel. Před integrací jde o rozdíl úhlových rychlostí, tj. relativní rychlost, takže výsledkem součtu (integrálu, sumy) bude relativní úhel Δα_1rel, tj. úhel měřený vůči střednímu Slunci jako nositeli střední rychlosti. A pokud Δα_1rel definuje úhel mezi Slunci, tak v rámci mapování časových souřadnic prostřednictvím úhlů toto Δα_1rel definuje zároveň i čas Δt = E₁ = – Δα_1rel (minus, viz další text).

Za hodinu (v rámci mapování časových souřadnic podle pohybu Slunce) považujeme úhel 15⁰, který urazí Slunce na nebi. A pokud jsme průběh funkce rychlostí odhadli jako cosinus, tak integrál z cosinu je sinus + konstanta.

Obvodové rychlosti, stejně jako úhlové rychlosti a sumární úhly, můžeme měřit přirozeně, ve směru ročního pohybu těles po ekliptice. Vzhledem ke stejnému směru denní rotace Země je zdánlivý pohyb těles (Sluncí) na obloze přesně opačný a má proto opačné znaménko (-Δα). Kladné relativní úhly na ekliptice jsou z pohledu pozorovatele na povrchu Země záporné, pořadí Sluncí procházejících například polednem se prohodí.

Konstanta, která se objeví po integraci, je ve shodě s předchozími úvahami o nastavení polohy středního Slunce, tj. o možném fázovém posunu středního Slunce. Z důvodu symetrie odchylek jí volíme jako nulovou. Nenulová hodnota znamená svislý posun celé křivky sinus nahoru nebo dolů, posun nulových bodů a vychýlení „střední hodnoty“.

Konstrukce funkce E₂

Funkce E₂ není tvořena Keplerovými zákony, ale polohou dvou kružnic a geometrií promítání pohybů těles mezi kružnicemi v prostoru. Po vystředování rychlostí pravého Slunce na rychlost 1. středního Slunce v rovině ekliptiky, jde o následný vztah průmětu rychlosti v_S1P v rovině nebeského rovníku k nové střední rychlosti v_S2.

Okamžité rychlosti v_S1P se i zde zkoumají jako relativní vůči střední rychlosti (v_S1P – v_S2), protože hledáme odchylku od středního času. Vzájemné rychlosti budou mít maxima v bodech zimních a letních slunovratů a stejně velká minima ve dnech jarní a podzimní rovnodennosti.

Další myšlenkový postup pro E₂ je stejný jako u E₁. Funkce rychlosti jako cosinus začíná v den zimního slunovratu před začátkem roku jako maximum (protože je tam průmět relativní rychlosti 1. středního Slunce z ekliptiky na nebeský rovník maximální) a spojitě přechází na minimum v bodě jarní rovnodennosti (protože je tam průmět relativní rychlosti 1. středního Slunce minimální). Funkce pak pokračuje očekávaným způsobem do dalších bodů (letní slunovrat a podzimní rovnodennost).

Úhel Δα_2rel navazuje na první úhel Δα_1rel. Princip je stejný, součtem (integrálem) součinů relativní úhlové rychlosti (ω_S1průmět – ω_S2) krát dt (časový interval) dostaneme relativní úhel Δα_2rel. Před integrací jde o rozdíl úhlových rychlostí, tj. relativní rychlost, takže výsledkem součtu (integrálu, sumy) bude relativní úhel Δα_2rel, tj. úhel měřený vůči 2. střednímu Slunci jako nositeli střední rychlosti.

Pokud Δα_2rel definuje úhel mezi Slunci, tak v rámci mapování časových souřadnic prostřednictvím úhlů toto Δα_2rel definuje zároveň i čas Δt = E₂ = – Δα_2rel. Pro znaménko platí stejný princip jako u funkce E₁. Integrací funkce cosinus je opět funkce sinus + konstanta.

I zde se po integraci objevila konstanta. Ta má stejný smysl jako u funkce E₁ a můžeme ji většinou zvolit jako nulovou.

Zajímavé je, že nová střední obvodová rychlost v_S2 je stejně velká jako první (v_S1), protože průmět oběhne rovníkovou kružnici za stejný čas jako jeho vzor ekliptiku a poloměry kružnic jsou stejné. Rozdíl je v tom, že druhé střední Slunce je na rovníkové kružnici oproti prvnímu fázově posunuté a fázový posun tu znamená další posun středního času.

Jednoduchým součtem dostaneme hledanou funkci Δt = E = E₁ + E₂ = – (Δα₁ + Δα₂). Tento časový rozdíl reprezentuje posun mezi pravým časem, odpovídajícím skutečnému (pravému) Slunci, a středním časem, reprezentovaným virtuálním středním Sluncem, tj. hodinkami. O zajímavé funkci E = E₁ + E₂ je celá následující podkapitola.

4. Funkce času E = E₁ + E₂ a rovnice času E = T_P – T_S

4.1 Graf a data pro funkci E

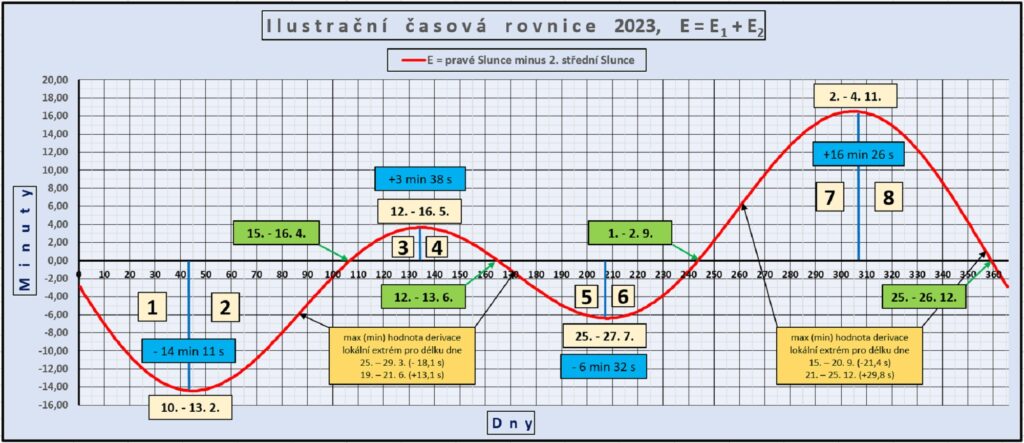
Nulovou hodnotou z minus na plus prochází křivka ve dnech 15. – 16. 4. (ve dnech 105 až 106), z plus na minus 12. – 13. 6. (ve dnech 163 až 164), z minus na plus 1. – 2. 9. (ve dnech 244 až 245) a z plus na minus ve dnech 25. – 26. 12. (ve dnech 359 až 360).

Hodnotu (-14 min 11 s) křivka dosahuje 10. – 13. února (dny 41 až 44), hodnotu (+3 min 38 s) 12. – 16. května (dny 132 až 136), hodnotu (-6 min 32 s) 25. – 27. 7. (dny 206 až 208) a hodnotu (+16 min 26 s) 2. – 4. listopadu (dny 306 až 308).

Záporná odchylka T_p – T_s (pravý – střední čas) znamená, že se pravé Slunce na obloze opožďuje a například pravé poledne nastane později než střední, kladná, že pravé poledne předchází střední. Jako příklady jsou uvedeny 2 varianty pro časový rozdíl 2 a 4 minuty.

12:00_P = 11:58_S + 2 min, E > 0
11:56_P = 12:00_S – 4 min, E < 0

4.2 Odchylky pravého poledne a pravého dne

Z astronomických tabulek je vidět, že největší záporná odchylka (kdy se pravé poledne za středním opožďuje) nastává v polovině února s hodnotou – 14 min 11 s, největší kladná odchylka (kdy pravé poledne předchází střednímu) nastává začátkem listopadu s hodnotou 16 min 26 s.

Nulové rozdíly (přibližné shody) mezi skutečnou délkou dne a střední hodnotou 24 hodin nastávají 4x ročně v „bodech“ lokálních extrémů funkce E (za 24 hod vznikne i tady malá odchylka). Shody mezi pravým polednem a středním nastávají v nulových bodech rovnice času také 4x ročně. Protože E je funkce času, ani tyto „shody“ nemusí nastat přesně ve 12:00 UT. Viz tabulka.

Jako zdroj astronomických hodnot byly použity tabulky (graf je ilustrační):
https://kalendar.beda.cz/hodnoty-casove-rovnice?year=2023

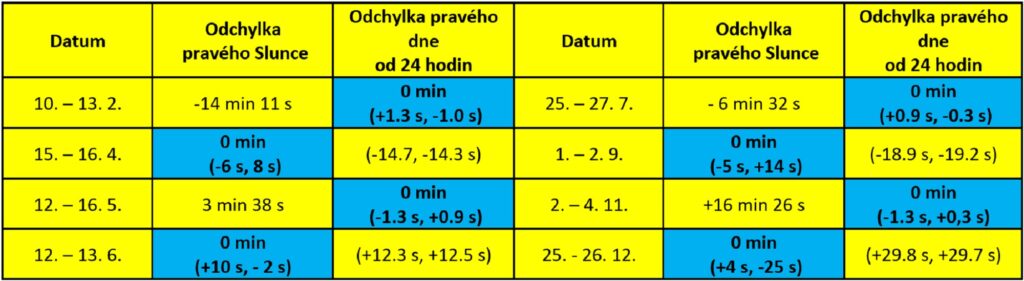
Pozn.: Nuly (vybarveno modře) představují ve skutečnosti interval, viz další text.

4.3 Je to funkce nebo rovnice? Platnost tabulky hodnot pro „rovnice času“

Pojem „rovnice času“ se v literatuře zobrazuje vždy jako graf funkce. Je to rovnice nebo funkce? Jaký je mezi těmito pojmy vztah? Na obrázku je funkce času E (t), v astronomických tabulkách je 365 hodnot E₁, E₂ a E pro rovnice E (t₀) = T_P (t₀) – T_S (t₀) pro pravé a střední poledne v průběhu roku. Hodnoty rovnic jsou průsečíky periodických časů „t₀ = 12:00 UT“ na ose x, a spojité funkce času E (t) na ose y. Funkce času E (t) udává neustále se měnící časový rozdíl mezi pravým a středním časem.  

Tabulky platí jen pro okamžiky UT = 12:00 (univerzální čas) pro 365 dní v roce a střední poledne nastanou v těchto časech jen v zóně UTC+0, a to jen na nultém centrálním poledníku. Ve zbytku pásma je sice střední čas dodefinován tzv. „standardizací“ podle referenčního centrálního poledníku, ale pravý i „reálný“ střední (lokální) čas se i tam spojitě mění. Střední lokální čas o 4 časové minuty na 1⁰ zeměpisné délky. Na každém dalším centrálním poledníku se tak poledne posune o 1 hod.

Jak ukazují grafy funkcí E₁, E₂ a E, změna hodnot je spojitá a nemění se skokem po 24 hodinách. Také se nemění jen časový rozdíl, mění se jak T_P, tak T_S. Dodefinování T_S na šířku časového pásma dle centrálního poledníku na tom nic nemění. Nečeká a nestojí nejen pravé Slunce, ale na místě nestojí ani střední Slunce. Obě Slunce se pohybují. Funkce E udává spojité změny vzájemných poloh Sluncí v průběhu roku. Hodnoty funkce E pro poledne v jiných časových pásmech a na různých zeměpisných délkách, nebo v jiných časech v průběhu dne se liší, protože poloha Sluncí se v čase spojitě mění.

Pro odchylky pravého poledne od středního v tabulkách často vidíme malou zápornou hodnotu v jeden den a jinou malou kladnou hodnotu následující den. Nulou tedy křivka často prochází v jiný čas než je poledne UT = 12:00, pravé a střední Slunce se v těchto případech setkají v jinou dobu než je uvedený čas. Není ani žádný důvod, proč by to muselo být přesně v okamžiku, kdy je k místu setkání Sluncí (v nulovém bodě  funkce E), natočen nultý meridián.

Přesnější hodnoty E pro jiné časy nebo pro poledne v různých pásmech je možné získat lineární interpolací mezi dvěma následujícími poledny UT = 12:00. V každém dalším časovém pásmu posunutém o hodinu jsou proto hodnoty pro poledne trochu jiné. Kdyby byly stejné a neměnily by se, nemohly by se změnit ani za 24 hodin.

Změna E za den je složena z malých změn za každou hodinu a minutu. Na druhé straně jsou tyto změny natolik malé, že většinou nemají v praxi velký význam. Tabulka hodnot E₁, E₂ a E pro UT = 12:00 ale rozhodně neplatí přesně pro všechna poledne ve všech pásmech UTC+X ani pro všechny časy v průběhu 24 hodin, platí jen pro čas UT = 12:00.

4.4 Obrázek výsledného pohybu Sluncí, který generuje časový rozdíl E

Obrázek zobrazuje vzájemné polohy 2. středního Slunce a pravého Slunce v rovině nebeského rovníku. Jedná se o pomalý roční pohyb těles. Současně existuje ještě mnohem rychlejší rotace Země kolem osy. Polohy jsou ilustrační a nezobrazují skutečné posunutí těles. Úhlové rozložení oblastí 1 – 8 je reálné. Nejviditelnějším důsledkem součtu křivek je rozpad původních symetrií.

Body setkání Sluncí jsou čtyři. Jedná se o nulové body funkce E. Na rozdíl od předchozích obrázků pro funkce E₁ a E₂, jsou tyto nové body rozmístěné asymetricky v dost nečekaných datumech, které se nevážou na žádný významný astronomický bod nebo jev (perihélium, slunovrat, rovnodennost atd.). Setkání Sluncí je ve dnech 24. – 25. 12. 2022 (začátek oblasti 1), 15. – 16. 4. 2023 (začátek oblasti 3), 12. – 13. 6. 2023 (začátek oblasti 5), 1. – 2. 9. 2023 (začátek oblasti 7), 25. – 26. 12. 2023 (další cyklus). Dva dny jsou uvedené proto, že jeden den je funkce pod nulou a druhý nad nulou (nebo obráceně). Není tam přesná nula pro poledne UT = 12:00 v jeden jediný den.

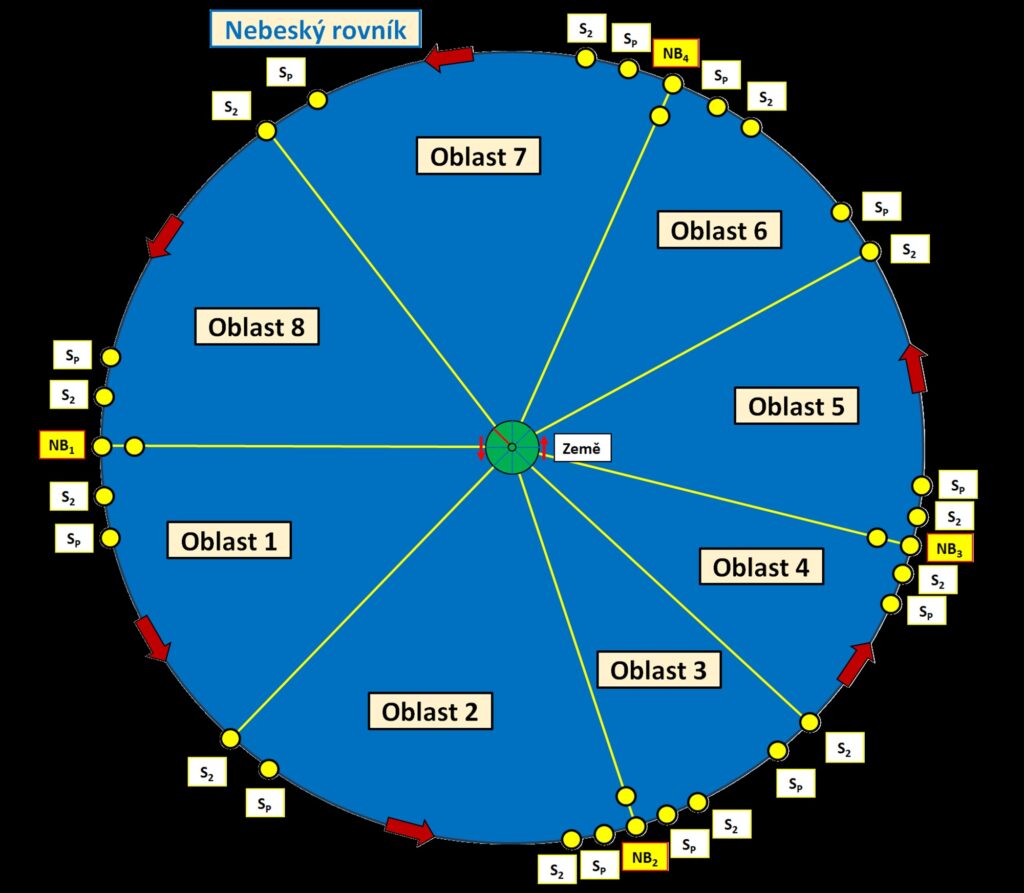
Popis značení na obrázku

S_P – pravé Slunce,
S₂ – 2. střední Slunce,
NB – setkání Sluncí, nulové body funkce E.

4.5 Komentář k obrázku pohybu Sluncí a k funkci E

Do grafu se promítají součty dvou podobných křivek typu (- sinus), jedné s 2x rychlejším průběhem fáze. Vztah mezi rychlostmi, polohami a časy je proto podobný jako v předchozích případech, odlišnost je v tom, že součtem křivek se naruší symetrie velikostí i poloh maxim a minim, stejně jako rozmístění nulových bodů. Ty se teď nacházejí z hlediska datumu v dost nečekaných bodech.

Oblasti 1 a 2

Vycházíme z 1. nulového bodu před začátkem roku, kde se S_P setká s S₂ a nastává shoda pravého poledne a středního. V NB₁ bude rychlost Slunce S_P výrazně větší (vyplývá to z grafu a předchozích úvah) než S₂, pravé Slunce proto S₂ hned za NB₁ předběhne. Vzdálenost mezi Slunci narůstá, ale rychlost S_P se postupně zmenšuje a v jistém okamžiku se rychlosti vyrovnají. Na grafu je to bod minima křivky E a začátek oblasti 2.

Vzdálenost mezi Slunci se přestane zvětšovat a v oblasti 2 po průchodu minimem křivky začne klesat, protože rychlost S_P bude už menší než S₂. Klesající rychlost S_P je spojena se zmenšujícím se E v oblasti 2. Slunce se navzájem přibližují, časový rozdíl klesá a v NB₂ se obě Slunce znovu setkají. Vliv 1. a 2. křivky (E₁ a E₂) je souhlasný, takže minimum E je výrazné.

V oblasti 1 a 2 je S_P před S₂, ale z důvodu rychlé rotace Země dochází k opačnému zdánlivému pohybu Sluncí na obloze vůči ročnímu pohybu těles po ekliptice. V meridiánu pozorovatele na Zemi bude nejdříve S₂ a až poté S_P. Vztah E = T_P – T_S2 bude záporný, E < 0. Pravé poledne zaostává za středním.

Oblasti 3 a 4

Vycházíme z NB₂, kde se S_P setká s S₂. V NB₂ je rychlost S_P menší než S₂, proto ho 2. střední Slunce hned za NB₂ předběhne. Vzdálenost mezi Slunci narůstá, ale rychlost S_P se postupně zvětšuje a v jistém okamžiku se rychlosti obou Sluncí vyrovnají. Na grafu je to bod maxima křivky E a začátek oblasti 4.

Vzdálenost mezi Slunci se přestane zvětšovat a v oblasti 4 po průchodu maximem křivky E začne klesat, protože rychlost S_P bude už větší než S₂ a S_P bude S₂ dobíhat. Rostoucí rychlost S_P je spojena se zmenšujícím se E v oblasti 4. Slunce se navzájem přibližují, časový rozdíl klesá a v dalším NB₃ se obě Slunce opět setkají. Vliv 1. a 2. křivky (E₁ a E₂) je tu protikladný, takže maximum E je menší.

V oblasti 3 a 4 je S₂ před S_P, ale z důvodu rychlé rotace Země vůči ročnímu pohybu bude v meridiánu pozorovatele na Zemi nejdříve S_P a až poté S₂. Vztah E = T_P – T_S2 bude kladný, E > 0. Pravé poledne předbíhá střední.

Oblasti 5 a 6

Vycházíme z NB₃, kde se S_P setká s S₂. V NB₃ je rychlost S_P větší než S₂, proto pravé Slunce 2. střední hned za NB₃ předběhne. Vzdálenost mezi Slunci narůstá, ale rychlost S_P se postupně zmenšuje a v jistém okamžiku se rychlosti vyrovnají. Na grafu je to bod minima křivky E a začátek oblasti 6.

Vzdálenost mezi Slunci se přestane zvětšovat a v oblasti 6 po průchodu minimem křivky začne klesat, protože rychlost S_P bude menší než S₂. Klesající rychlost S_P je spojena se zmenšujícím se E v oblasti 6. Slunce se navzájem přibližují, časový rozdíl klesá a v dalším NB₄ se obě Slunce opět setkají. Vliv 1. a 2. křivky (E₁ a E₂) je protikladný, takže minimum E je menší.

V oblasti 5 a 6 je S_P před S₂, ale v meridiánu pozorovatele na Zemi je nejdříve S₂ a až poté S_P. Vztah E = T_P – T_S2 je záporný, E < 0. Pravé poledne zaostává za středním.

Oblasti 7 a 8

Vycházíme z NB₄, kde se S_P setká s S₂. V NB₄ je rychlost S_P menší než S₂, proto ho 2. střední Slunce hned za NB₄ předběhne. Vzdálenost mezi Slunci narůstá, ale rychlost S_P se postupně zvětšuje a v jistém okamžiku se rychlosti obou Sluncí vyrovnají. Na grafu je to bod maxima křivky E a začátek oblasti 8.

Vzdálenost mezi Slunci se přestane zvětšovat a v oblasti 8 po průchodu maximem křivky začne klesat, protože rychlost S_P bude už větší než S₂. Rostoucí rychlost S_P je spojena se zmenšujícím se E v oblasti 8. Slunce se navzájem přibližují, časový rozdíl klesá a v dalším NB₅ se obě Slunce opět setkají. Vliv 1. a 2. křivky (E₁ a E₂) je souhlasný, takže maximum E je výrazné.

V oblasti 7 a 8 je S₂ před S_P, ale z důvodu rychlé rotace Země vůči ročnímu pohybu bude v meridiánu pozorovatele na Zemi nejdříve S_P a až poté S₂. Vztah E = T_P – T_S2 bude kladný, E > 0. Pravé poledne předbíhá střední.

4.6 Nejkratší a nejdelší den v roce, inflexní body funkce E

Inflexní body funkce E jsou body, kde má 1. derivace lokální extrém. Odchylky délky dne od 24 hod tam nabývají lokální maxima nebo minima (změny E, tj. ∆E, jsou v nich maximální).

Inflexní body jsou místa, kde se měnící úhel tečny křivky E při pohybu po její linii zastaví a začne otáčet opačným směrem, proto mají derivace funkce v těchto bodech lokální extrém. Maximální kladné nebo záporné odchylky pravého dne od 24 hodin se tak nachází v bodech, které jsou oproti nulovým bodům funkce E posunuté. To je dost překvapující a pravým důvodem je asymetrie funkce E.

U goniometrických funkcí jako sinus nebo cosinus platí, že pokud například u funkce sinus hledáme maximální nebo minimální hodnoty derivací (lokální extrémy směrnice křivky), už při pohledu na průběh křivky i bez výpočtu vidíme, že maximální a minimální hodnoty derivací budou v nulových bodech původní křivky sinus. Právě symetrie funkce sinus, která reprezentuje symetrie rychlostí a vzdáleností pohybujících se těles, je důvodem, proč se inflexní body ztotožní s nulovými body a k setkání Sluncí dochází v bodech jako je perihélium, afélium, slunovraty nebo rovnodennosti.

U „rovnice času“ jsou hodnoty lokálních extrémů funkce E asymetrické, a proto nejsou maxima a minima směrnice tečny a nulové body funkce E totožné, viz předchozí graf a následující tabulka. Hodnoty E tvoří součet goniometrických funkcí, a navíc s různým průběhem fáze, takže i vlastnosti výsledného součtu jsou jiné než u jednoduchého sinu nebo cosinu. Rozložení inflexních bodů je takové, že ani neumožňuje ztotožnění s nějakými „jinými“ nulovými body „posunuté“ funkce E.

A protože je výsledné E součtem dvou funkcí sinus, kde platilo, že součet kladných odchylek je roven součtu záporných, platí to i pro součet funkcí E₁ + E₂. Kladné a záporné hodnoty funkce E se v součtu vynulují. Inflexní body se ale do nulových kvůli tomu „nepřestěhují“.

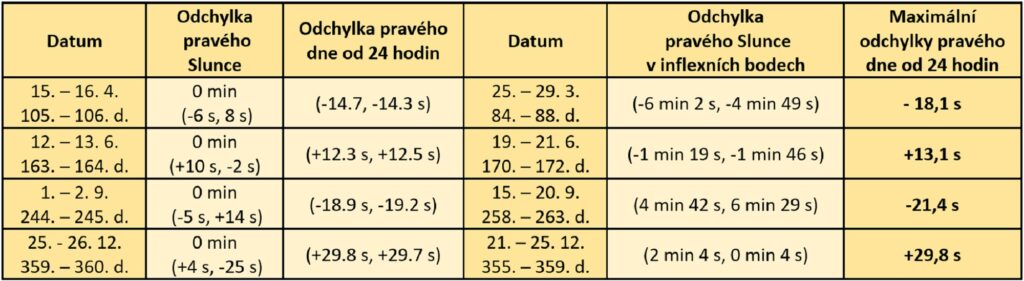
V tabulce jsou uváděné vždy krajní hodnoty v daném časovém intervalu, protože funkce E se v čase mění. Nulový bod funkce sice je v nule, ale nemusí to být (a většinou ani není) přesně v době středního poledne UT = 12:00.

V roce 2023 nastaly nejdelší dny v roce s délkou (24 hod + 29,8 s) 21. – 25. prosince, nejkratší dny s délkou (24 hod – 21,4 s) 15. – 20. září. Rozdíl mezi nejkratším a nejdelším dnem je asi 51 s. Vzhledem k plochým lokálním extrémům je uvedeno několik dnů se stejnou hodnotou.

4.7 Délka dne a odchylky od 24 hodin graficky

Kde jsou v jednotlivých rovnicích času nebo v hodnotách funkce E schované délky dne, případně odchylky délky dne od 24 hodin? Tyto informace se nachází v přírůstku nebo úbytku hodnot funkce E. Ani funkce, ani jednotlivé rovnice času neukazují délky dne, resp. odchylky délky dnů od 24 hod přímo. Pro pravý den, dlouhý celoročně přesně 24 hod, bychom žádnou „rovnici času“ nepotřebovali, protože pravé Slunce by se ztotožnilo se středním (T_P = T_S a E (t) = 0).

Z rovnic času a funkce času je vidět, že v bodech lokálních extrémů (maxim a minim) se hodnota E (tj. hodnota časového rozdílu mezi pravým a středním Sluncem) „nemění“. Pokud se časový rozdíl v průběhu otočení Země nemění, znamená to, že reálná rotace vůči pravému Slunci je stejně dlouhá jako ta střední vůči střednímu Slunci, a ta trvá 24 hodin. Kdyby byla jiná, tak by se poloha pravého Slunce vůči střednímu posunula (u pevného tělesa se otočí všechny body o stejný úhel).

Z tohoto důvodu má den „přesně“ 24 hodin jen v bodech maxim a minim uvedené funkce času, to je 4x ročně, protože právě tam se odchylka pravého Slunce od středního nemění. Bohužel to platí jen „bodově“. Slovo „nemění“ tu znamená jen to, že se přírůstek mění na úbytek (a opačně), takže změna (derivace) prochází nulou. Změny ale nejsou diskrétní a nemění se skokově až po 24 hodinách, jsou spojité a malé odchylky vzniklé za 24 hod vznikají i v těchto dnech, protože nulová změna funkce E netrvá celých 24 hodin.

Absolutně přesně 24 hodin nemá ani jeden den v roce, ale čtyři dny se tomu hodně přibližují.

Ve všech dalších bodech funkce času E mimo lokálních extrémů, se vzdálenost Sluncí mění a pravé poledne se každý den posouvá vůči střednímu právě proto, že „pravý den“ nemá 24 hodin. To znamená, že ani samotná rotace Země kolem osy měřená vůči Slunci není přesným etalonem pro měření času. Z hlediska běžného života a vnímání času rozdíl v délce dne není příliš velký, je to v průběhu roku „jen“ asi ± ½ minuty a člověk tak malé změny nevnímá.

Jsou za odchylkami délky dne změny v setrvačníkové rotaci?

Země se víceméně točí stále stejně a rozdíly v otáčení Země jako setrvačníku jsou minimální. Hvězdný den se v průběhu jednoho roku prakticky nemění, resp. změny jsou velmi malé. Zdrojem problémů je rotace Země měřená vůči Slunci.

Délka dne je prodloužená nebo zkrácená kvůli změnám v tzv. „proti-rotaci“. Za tu jsou odpovědné změny rychlosti pohybu Země kolem Slunce důsledkem Keplerových zákonů a změny v průmětu pohybu 1. středního Slunce z roviny ekliptiky do roviny rovníku. Sklon rovin je důsledkem odklonu osy rotace Země (původně kolmé k rovině ekliptiky) o 23,5⁰ po srážce nebeských těles v dávné minulosti.

Rozhodně to není tak, že by zeměkouli něco roztáčelo, a pak zase brzdilo. Nejde o změny v setrvačníkové rotaci. Na druhou stranu je pravdou, že délka dne měřená vůči Slunci je opravdu někdy delší a jindy kratší. Není to nějaký klam nebo pouhé zdání. 

Představa o délce dne z hlediska pohybu Sluncí na obloze

Předcházející obrázek vzájemného pohybu Sluncí ukazuje pohyb těles po nebeském rovníku pozorovaný z bodu nad celou soustavou těles (z nebeského pólu). Polohy Sluncí jsou na obrázku zobrazené ve všech důležitých pozicích v průběhu roku. Jsou to body, kde dochází k setkání Sluncí, k vzájemnému předbíhání nebo k maximální vzájemné vzdálenosti těles, tj. ke změně vzdalování na přibližování. Úhlovou vzdálenost mezi Slunci reprezentuje E.

Trochu složitější je představa, jak se vlastně pohyby těles na nebeské sféře budou promítat do ΔE, případně jak se budou lišit pozorování v soustavě rotující spolu se Zemí od pozorování z hlediska pevné nerotující nebeské sféry. V obou případech (i když pokaždé trochu jinak) se do pohybu promítnou dvě složky: roční a denní. První složkou je pomalý roční pohyb Sluncí po nebeském rovníku. Druhou je rychlý denní pohyb po obloze způsobený rotací Země.

Pohled z bodu nad nebeským rovníkem (z nerotujícího nebeského pólu)

Pravé Slunce se v oblastech s kratším pravým dnem (2 – 3 a 6 – 7) pohybuje po nebeském rovníku pomaleji než střední a v oblastech s delším dnem (1, 4 – 5 a 8) zase rychleji. To se může zdát paradoxní, protože někdo by mohl mít pocit, že když pravé poledne nastane ve dvou následujících dnech rychleji než střední, tak by se pravé Slunce mělo pohybovat rychleji než střední.

Jedno i druhé je pravdou, Slunce bude rychlejší i pomalejší, vše závisí na tom, z jaké pozorovací soustavy se díváme. Z povrchu Země se některé věci jeví jinak než z nebeského pólu. I ze zámku a z podzámčí věci vypadají různě. Do pohybu těles po nebeském rovníku je z pohledu pozemského pozorovatele vnesen nový „nevnímaný“ pohyb – rotace Země. Ta změní celou řadu veličin: pořadí těles, velikost a směr rychlostí těles, a dokonce i úhly.

Trochu nečekaná a paradoxní skutečnost, že větší rychlost pohybu znamená delší den, je způsobena tím, že se při pohybu Země kolem Slunce „z pohledu pólu“ sčítají dva úhly odlišného charakteru. První úhel je od rotace Země. Tam platí, že rychlejší rotace (větší rychlost oběhu Slunce kolem Země) znamená kratší den. Čím rychleji Země rotuje, tím rychleji Slunce „oběhne kolem Země“ a pravý den bude kratší.

Druhý úhel v součtu je od proti-rotace. Ta má původ v pohybu Země po oběžné dráze kolem Slunce a působí opačně. Čím je pohyb „pravé“ Země (a promítaného pravého Slunce) rychlejší, tím větší úhel proti-rotace vznikne a Země se musí víc dotáčet, takže den je delší. Rozdíl mezi pravým a středním Sluncem je tvořen právě touto složkou pohybu. Proto tu platí logika, čím větší rychlost, tím delší den, čím menší rychlost, tím je den kratší.

Pravý den je doba otočení zvoleného meridiánu na Zemi vůči pravému Slunci, které se pohybuje po nebeském rovníku. Pravý den bude kratší než střední, když se Země vůči pravému Slunci otočí rychleji (za kratší čas) než vůči střednímu (a delší, když se vůči pravému Slunci bude otáčet déle než vůči střednímu). Na vzájemné poloze Sluncí nezáleží, nejde o to, které Slunce je vepředu, a které poledne bude dříve, zda pravé nebo střední.

Protože se Země otáčí ze dne na den stále stejně (rotace je konstantní), je toho možné dosáhnout jen tak, že úhel otočení Země od jednoho pravého poledne do druhého bude menší než stejný úhel pro střední poledne (α_P < α_S). Pokud bude rychlost pravého Slunce zaostávat za rychlostí středního, meridán se k němu dotočí rychleji. Úhel rotace Země od jednoho pravého poledne do druhého bude z důvodu tohoto dotáčení větší než 360⁰ (v průměru cca 361⁰).

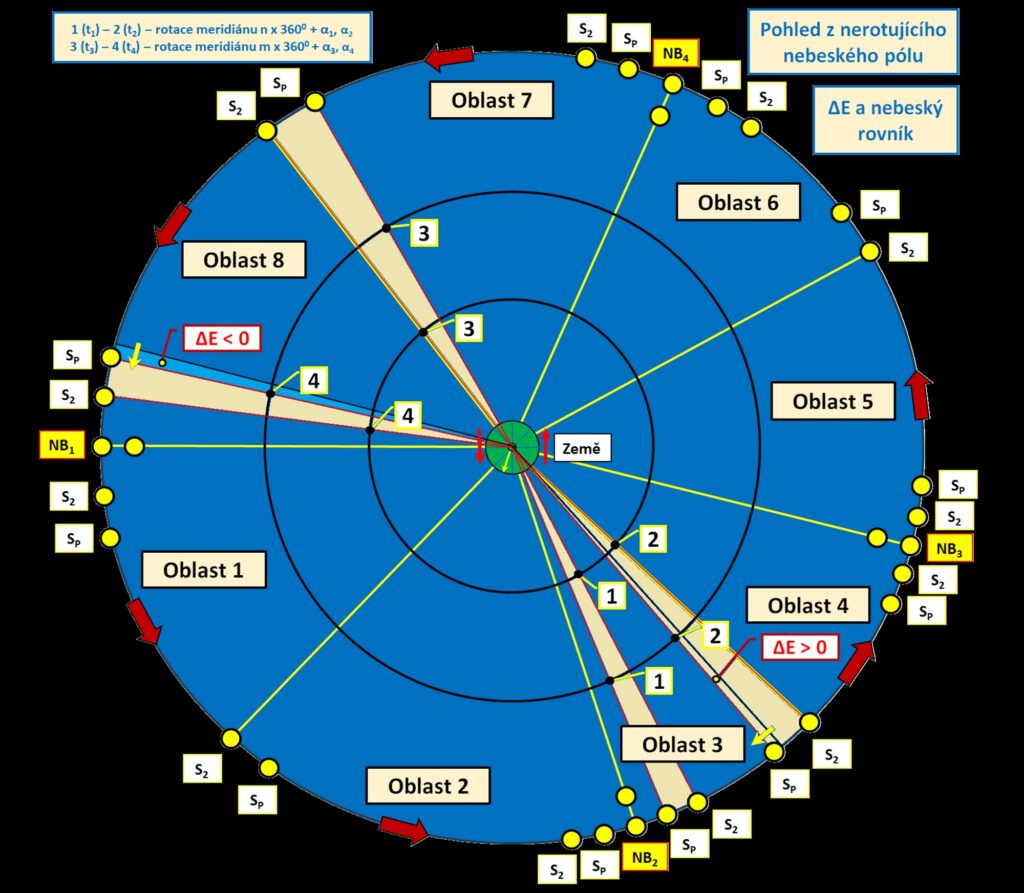
Legenda k obrázku

Znaménko ΔE není určeno pořadím Sluncí, ale změnou funkce E. Nejlépe je to vidět na dřívějším obrázku výsledné funkce E (grafu „rovnice času“). Například v oblasti 2 je pravé Slunce pozadu za středním, v oblasti 3 je pravé Slunce před středním, ale ΔE je v obou případech  kladné (derivace funkce E je kladná). V oblastech 2 – 3 tak platí, že den je kratší, protože odchylka délky pravého dne je (– ΔE), viz text o podkapitolu dál (matematické vyjádření délky pravého dne).

„Menší vopruz“ ohledně znamének je v tom, že úhly měřené na obrázku z pohledu nerotujícího nebeského pólu jsou měřené („logicky“) proti směru hodinových ručiček, tj. opačně než při pohledu pozorovatele oblohy na Zemi, ale E a ΔE definují úhly, které měří pozorovatel na Zemi jako úhly mapující časy pravého a středního Slunce na obloze. Úhlům na nebeském rovníku tak musíme přiřadit navíc znaménko minus.

ΔE = E (t₂) – E (t₁) = – (Δα_2rel – Δα_1rel) = – ((α_P (t₂) – α_S2 (t₂)) – (α_P (t₁) – α_S2 (t₁)))

Výsledné znaménko úhlu rozdílu dvou rozdílů úhlů se změní na opačné, protože chceme dostat ΔE. Například v oblastech 2 – 3 se přechodem do soustavy pozorovatele na Zemi znaménko změní z minus na plus a  ΔE > 0. Odchylka délky dne bude ale záporná, protože odchylka je rovná hodnotě (– ΔE), takže den bude kratší.

Pozorovatel na Zemi

Trochu odlišné jsou úvahy o výsledném pohybu Sluncí vůči pozorovateli na Zemi. Celý cyklický pohyb po nebeském rovníku se uskuteční za jeden rok. Vzájemný roční pohyb Sluncí není z pohledu pozorovatele na otáčející se Zemi moc výrazný. V průběhu jediného dne se uskuteční jen velmi malý vzájemný posun Sluncí, střední Slunce je navíc jen virtuální. Hlavní pohyb těles na obloze je od rotace Země podobně jako u hvězd nebo Měsíce.

Odlišná je i orientace úhlů, protože pohyb těles má vůči pozorovateli „na stojící pevné Zemi“ opačný směr. Slunce se na obloze pohybují od východu na západ, proti směru jejich pohybu na nebeském rovníku. Proto se změní i pořadí Sluncí. Co bylo na konci, bude na začátku, a co bylo na začátku, bude na konci.

Změní se také velikost a směr rychlostí. Pokud se jedno Slunce na nebeském rovníku pohybuje rychleji než druhé, pro pozorovatele na Zemi bude naopak pomalejší. Když bude například rychlost pravého Slunce na nebeském rovníku v_P < v_S, tak výrazně větší opačná rychlost obou Sluncí od rotace Země v_R se o tyto dvě „malé“ rychlosti pouze zmenší a nerovnost se zamění:

v_P´ > v_S´, kde v_P´ = (v_R – v_P) a v_S´ = (v_R – v_S)

Rychlejší na obloze bude původně pomalejší pravé Slunce s novou rychlostí v_P´ = (v_R – v_P). Dříve rychlejší střední Slunce bude mít novou rychlost v_S´ = (v_R – v_S). Vzhledem k velkému rozdílu úhlových rychlostí denního a ročního pohybu a malým rozdílem mezi rychlostmi v_P a v_S, to bude po 24 hodinách jen velmi malá, ale zato podstatná změna vzájemných poloh Sluncí. Charakterizuje ji hodnota funkce ∆E, která určuje odchylku délky pravého dne od 24 hod. Maximální odchylka je v průběhu roku menší než ±1/2 minuty. Hodnoty ∆E  se proto pohybují v sekundách. Jedna časová sekunda je 15 úhlových sekund.

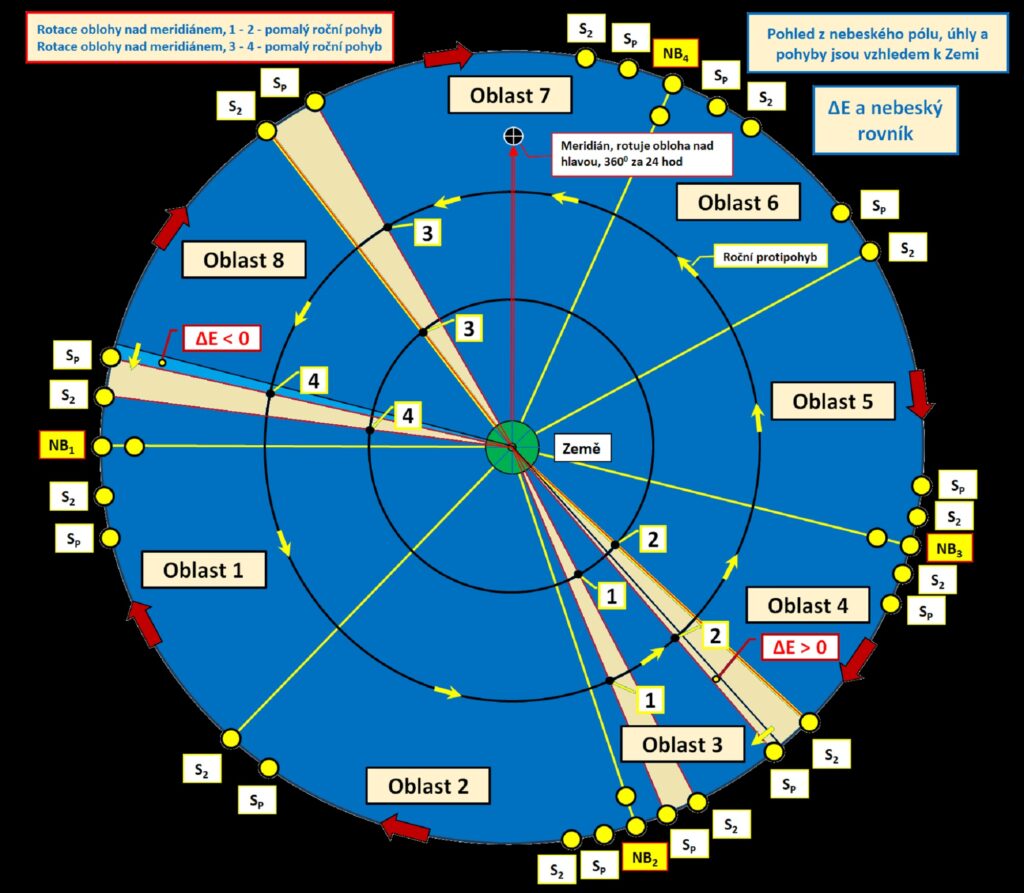
Legenda k obrázku

Ve druhém případě se z pohledu pozorovatele na Zemi měří hodinový úhel od meridiánu, kde je definována nula, ve směru zdánlivého pohybu hvězd, tj. směrem na západ. V okamžiku kulminace nebeského objektu (poledne) je hodinový úhel nulový, 15⁰ definuje hodinu (1⁰ jsou 4 časové minuty).

Úhly na obrázku bude pozorovatel na Zemi měřit ve směru hodinových ručiček. Poloha Sluncí č. 1 odpovídá času t₁, poloha Sluncí č. 2 odpovídá času t₂. Podobně je to u poloh 3 a 4 s časy t₃ a t₄.

ΔE = E (t₂) – E (t₁) = ((T_P (t₂) – T_S (t₂)) – (T_P (t₁) – T_S (t₁))) = (Δα_2rel – Δα_1rel) = ((α_P (t₂) – α_S2 (t₂)) – (α_P (t₁) – α_S2 (t₁)))

Výsledné znaménko úhlu rozdílu dvou rozdílů úhlů se tady měnit nemusí. Měřené úhly přímo mapují čas  podle geometrického úhlu na obloze. Například v oblastech 2 – 3 výsledný úhel vychází kladný a ΔE > 0. Odchylka délky dne bude ale vždy (– ΔE), takže den je v oblastech 2 – 3 o hodnotu ΔE kratší.

4.8 Rovnice času a matematika funkcí E (t) a ΔE (t)

Platí rovnice E = T_P – T_S. Tuto rovnici napíšeme pro dva různé okamžiky, kdy pravé Slunce projde 2x po sobě meridiánem. Nejdříve první den v okamžiku t₁, a pak druhý den v okamžiku t₂.

T_P a T_S jsou souřadnice času pro stejný okamžik v různých časových soustavách, na „různých hodinkách“ a znamenají rovnici: E (t) = T_P (t) – T_S (t).

Po dalších úpravách dostaneme:

ΔE = E (t₂) – E (t₁) = (T_P (t₂) – T_S (t₂)) – (T_P (t₁) – T_S (t₁))
ΔE = (T_P (t₂) – T_P (t₁)) – (T_S (t₂) – T_S (t₁))

Délku pravého dne, tj. opakovaný průchod pravého Slunce meridiánem (24 hod_prav), určují souřadnice (T_P (t₂) – T_P (t₁)). Jsou to časy v periodických souřadnicích, opakující se každý den v intervalu od nuly do 24 hod_prav (pravého času). Pokud měříme den od jednoho pravého poledne do druhého, tak je to 12:00_P první den a 12:00_P následující den. Rozdíl časových souřadnic je nulový.

V souřadnicích středního času tomuto intervalu jednoho pravého dne přísluší okamžiky T_S (t₁), T_S (t₂) a časový interval: (T_S (t₂) – T_S (t₁))_int. Okamžiky t₁, t₂ mohou být časy v soustavě středního času nebo i v jiných časových soustavách. Pak platí:

ΔE = (T_P (t₂) – T_P (t₁)) – (T_S (t₂) – T_S (t₁)) = 0 – (T_S (t₂) – T_S (t₁)).

Časový rozdíl na „středních“ hodinách ve dvou následujících dnech určuje nulovou, kladnou nebo zápornou odchylku od 24hodinového středního dne.

Odchylka délky pravého dne od 24 hod_S je: (T_S (t₂) – T_S (t₁)) = – ΔE.
Pravý den je v souřadnicích středního času dlouhý (24 hod – ΔE).

Příklad 1 pro periodické souřadnice (časový interval do 24 hod)

E₂ = (T_P (t₂) – T_S (t₂))                   {00:10} = 12:00_P – 11:50_S, kde {00:10} jsou souřadnice (hod:min)
E₁ = (T_P (t₁) – T_S (t₁))                   {00:05} = 12:00_P – 11:55_S

ΔE = (T_P (t₂) – T_P (t₁)) – (T_S (t₂) – T_S (t₁)) = 0 – (T_S (t₂) – T_S (t₁))
ΔE = {00:05} = (12:00_P – 12:00_P) – (11:50_S (t₂) – 11:55_S (t₁)) = – 11:50_S (t₂) + 11:55_S (t₁)

První den nastalo pravé poledne v 11:55_S, druhý den v 11:50_S. Odchylka pravého dne od středního je (T_S (t₂) – T_S (t₁)) = (- ΔE_S), a to je (- 5 min_S). Pravý den je o 5 běžných minut kratší (jde o souřadnice T_S).

V předchozích úvahách jde o rovnost časových souřadnic, intervaly si rovné nejsou, od jednoho dne 11:55 do druhého dne 11:50 určitě neuplynulo jen 5 min středního času.

Příklad 2 pro neperiodické souřadnice (časový interval nad 24 hod)

E₂ = (T_P (t₂) – T_S (t₂))                   {00:10} = 12:00_P – 11:50_S = 36:00_P – 35:50_S
E₁ = (T_P (t₁) – T_S (t₁))                   {00:05} = 12:00_P – 11:55_S = 12:00_P – 11:55_S

Délka pravého dne mezi okamžiky (t₂ – t₁) je: (T_P (t₂) – T_P (t₁))_int = (T_S (t₂) – T_S (t₁))_int, jinak zapsáno:

((t₂)_TP – (t₁)_TP)_int = ((t₂)_TS – (t₁)_TS)_int, na rozdíl od příkladu 1, zde porovnáváme intervaly, ne souřadnice

(36:00_P – 12:00_P)_int = (35:50_S – 11:55_S)_int,
kde(t₂)_TP, (t₁)_TP, (t₂)_TS a (t₁)_TS jsou časy v souřadnicích pravého a středního času.

Pravý den = (24:00_P)_int = (24:00_S – (11:55_S -11:50_S))_int, jde o rovnost časových intervalů.

Pravý den = (24:00_P)_int = (24:00_S – ΔE_S)_int, časové souřadnice si jako čísla rovné nejsou.

Jak je z obou příkladů vidět, rovnice ΔE = (T_P (t₂) – T_P (t₁)) – ((T_S (t₂) – T_S (t₁)) udává nerovnost plynutí časových souřadnic na dvou „různých hodinkách“, středních a „pravých“ a Δ {E} určuje jejich rozdíl.

Časový interval určuje Δt = (t₂ – t₁). Na „pravých“ hodinkách to bude interval ohraničený souřadnicemi (T_P (t₂) – T_P (t₁))_int, na „středních“ hodinkách to bude interval definovaný rozdílem časových souřadnic (T_S (t₂) – T_S (t₁))_int. Rovnost dvou intervalů s různými čísly zajistí různě dlouhé jednotky času.

Jak je vidět z obou příkladů, jsou tedy možné dva pohledy: Na rovnici se můžeme dívat jako na rovnost čísel (pak tato čísla mají význam souřadnic v různých časových soustavách a do rovnice potřebujeme ΔE), nebo jako na rovnost časových intervalů, které odpovídají časovým souřadnicím, pak ΔE můžeme vynechat,protože mluvíme o intervalu Δt = (t₂ – t₁).

Dvě rovnice

(1) Rovnice (T_P (t₂) – T_P (t₁))_int = (T_S (t₂) – T_S (t₁))_int platí ve smyslu časového intervalu (t₂ – t₁) určeného ve dvou různých časových soustavách. Jinak zapsané je to: ((t₂)_TP – (t₁)_TP) = ((t₂)_TS – (t₁)_TS), kde (t₂)_TP, (t₁)_TP, (t₂)_TS a (t₁)_TS jsou časy v souřadnicích pravého a středního času. Souřadnice T_P (t₂), T_S (t₂) ani příslušné rozdíly z úvodu odstavce si číselně rovné nejsou, časové intervaly (tj. čísla s fyzikálními jednotkami) ano. Tato rovnice udává rovnost dvou časových intervalů. U délky by to byla např. rovnice 1 km = 1000 m, rovnost platí pro délky, čísla si rovné nejsou (1000 ≠ 1).

(2) Rovnice ΔE = (T_P (t₂) – T_P (t₁)) – (T_S (t₂) – T_S (t₁)) udává nerovnost plynutí časových souřadnic mezi různými hodinkami a Δ {E} určuje jejich rozdíl. U délky by to byla například rovnice: {999} = (1 000_m)_souř – (1_km)_souř. V případě intervalů pro pravý a střední čas rozdíl mezi jednotkami není tak dramatický.

Vzhledem k tomu, že časové souřadnice na pravé straně definují časové intervaly, je jasné, že i Δ {E} musí reprezentovat nějaký časový interval, ale interval Δt = (t₂ – t₁) to určitě není. Bude to nějaká časová změna, která se odehrává v takto definovaném čase (t₂ – t₁).

Problém se souřadným systémem T_P

Souřadný systém T_P je možné využít prakticky jen na definici délky pravého dne, jak to bylo uděláno v příkladě č. 2. Nelze tam definovat plnohodné „hodinky 2“. Nejen, že tyto hodinky jdou jinak než střední, ale ony nejdou stabilně, pravý čas mapovaný podle geometrického úhlu tiká každý den jinak, dokonce každou hodinu, minutu nebo sekundu. Intervaly „tiků“ nejsou konstantní.

Jde o „klouzavý“ čas (časový systém), kde se jednotka času spojitě mění (24 hod_prav je každý den jiný časový interval). Z tohoto důvodu je měření intervalu (t₂ – t₁) určeného souřadnicemi ((T_P (t₂) – T_P (t₁)) jinak než na definici doby od jednoho poledne do druhého těžko použitelné. Tyto hodinky jsou absolutně nestabilní.

Rovnice (T_S (t₂) – T_S (t₁)) = – ΔE, definuje odchylku pravého dne od středního v běžných „středních“ jednotkách a znamená, že jeden konkrétní pravý den o 24 pravých hodinách je dlouhý (24:00_S – ΔE)_int. „Pravé hodiny“ mají každý den a každou hodinu jinou délku.

Problém kombinace různých souřadných soustav

Ve dvou specifických případech nastanou v rovnici jednoduché výsledky:

(1) posun Sluncí měříme v době pravého poledne, to znamená, že si zaznamenáme polohy středního Slunce při dvou následujících průchodech pravého Slunce meridiánem.

ΔE = (T_P (t₂) – T_P (t₁)) – (T_S (t₂) – T_S (t₁)) = (12:00_P -12:00_P) – (T_S (t₂) – T_S (t₁))

ΔE = – (T_S (t₂) – T_S (t₁)), ΔE je pak v souřadnicích středního času. Časy a jím příslušné úhly patří k střednímu času.

(2) posun Sluncí měříme v době středního poledne, to znamená, že si zaznamenáme polohy pravého Slunce při dvou následujících průchodech virtuálního středního Slunce meridiánem.

ΔE = (T_P (t₂´) – T_P (t₁´)) – (T_S (t₂´) – T_S (t₁´)) = (T_P (t₂´) – T_P (t₁´)) – (12:00_S – 12:00_S)

ΔE = (T_P (t₂´) – T_P (t₁´)) a ΔE bude v souřadnicích pravého času. Časy a jim příslušné úhly budou patřit k pravému času.

V ostatních případech půjde o kombinaci čísel (souřadnic). Označme pro obecné t₁ a t₂:
(T_S (t₂) – T_S (t₁)) = ΔE_S (t₁, t₂) = ΔT_S (t₁, t₂), plynutí souřadnic středního času mezi okamžiky t₁, t₂
(T_P (t₂) – T_P (t₁)) = ΔE_P (t₁, t₂) = ΔT_P (t₁, t₂), plynutí souřadnic pravého času mezi okamžiky t₁, t₂

Rovnice:
ΔE = (T_P (t₂) – T_P (t₁)) – (T_S (t₂) – T_S (t₁)) pro obecné t₁ a t₂ se dá přepsat:

ΔE (t₁, t₂) = (ΔE_P (t₁, t₂) – ΔE_S (t₁, t₂)) a znamená číselnou rovnost souřadnic, (značeno {}). Rovnice s ΔE pro intervaly času neplatí, protože: (T_P (t₂) – T_P (t₁))_int – (T_S (t₂) – T_S (t₁))_int = 0, ale (ΔE)_int ≠ 0 (obecně ≠ 0).

Ve všech časech je ΔE složeno vždy ze dvou příspěvků souřadnic {}: Δ {E_P}, Δ {E_S} a Δ {E} = (Δ {E_P} – Δ {E_S}). V předchozích dvou probíraných případech z rovnice pouze jeden nebo druhý člen vypadne pro periodické souřadnice (odečtem 24 pravých nebo středních hodin).

Rovnice Δ {E} (t₁, t₂)} = (Δ {E_P} (t₁, t₂) – Δ {E_S} (t₁, t₂)) je zvláštní rovnicí. Rovnost souřadnic generuje 3 časové intervaly svázané s těmito souřadnicemi, tj. intervaly příslušné k souřadnicím Δ {E}, Δ {E_P} a Δ {E_S}. Většinou časové intervaly na sebe navazují. Když z Prahy do Bratislavy přes Brno dojedu za 3 hodiny a z Brna do Bratislavy za hodinu, tak z Prahy do Brna to bude rozdíl obou časů, tj. za 2 hodiny.

Třetí čas tady ale znamená něco úplně jiného.  Ani při měření na obloze v podobě geometrického úhlu jako ekvivalentu k ΔE, tento úhel netvoří žádnou následnost dějů a ΔE vzniká současně s oběma dalšími úhly ΔE_P a ΔE_S. Je to jako kdybychom cestu z Prahy do Bratislavy změřili dvěma různými hodinkami a z rozdílu na číselnících pak dokázali určit novou časovou charakteristiku.

Znaménko ΔE

I když letmý pohled na rovnice v bodech (1) a (2) výše vzbuzuje dojem, že znaménko ΔE závisí na tom, zda polohu Sluncí (čas) měříme dva dny po sobě v pravé nebo střední poledne, není to tak, znaménko se zachovává dle základní definice E = T_P (t) – T_S (t), opačné by bylo jen pro E = T_S (t) – T_P (t).

Příklad – pravé poledne je před středním a pravý den je delší, měření ve 12:00_P a 12:00_S  

E₂ = 12:00_P – 11:50_S                 přibližně platí                   E₂ = 12:10_P – 12:00_S
E₁ = 12:00_P – 11:49_S                                                             E₁ = 12:11_P – 12:00_S
E₂ – E₁ = – 11:50_S + 11:49_S = -1_S                                          E₂ – E₁ = – 12:10_P + 12:11_P = -1_P                     

Znaménko E i ΔE a pořadí, ve kterém nastávají poledne, ani délka dne se tím samozřejmě nemohou měnit. Malá odlišnost bude ve velikosti intervalů, protož jednotky pravého času nejsou stejně dlouhé jako jednotky středního času:
(-1_S)_int ≠ (-1_P)_int, ale {-1_S}_souř = {-1_P}_souř.

Zpět k rovnici E (t) = T_P (t) – T_S (t)

Při běžném letmém pohledu na „rovnici času“ nejsou vidět všechny souvislosti této rovnice. Vztah se tradičně prezentuje jen jako součet nějakých časových intervalů: k času na hodinkách podle uvedené rovnice přičteme nebo odečteme podle astronomických tabulek minuty a sekundy a dostaneme dobu, kdy nastane pravé poledne. To nevypadá složitě, ale vztah veličin času je ve skutečnosti obecně komplikovanější, protože obsahuje součet souřadnic v různých časových soustavách a interpretace je proto složitější. Např.:

(1)          {00:10} (10 min) = 12:00_P – 11:50_S, 00:10 je zápis časových souřadnic, ne tradiční čas
Z logiky časové následnosti plyne, že pokud pravé poledne nastalo v 11:50 středního času, tak střední poledne nastane ve 12:00_S, tj. za 10 středních minut. Interval času₁ mezi poledny je 10 min_S.

(2)          {00:10} (10 min) = 12:10_P – 12:00_S
Pokud střední poledne nastalo ve 12:10_P, tak pravé muselo nastat ve12:00_P, to znamená před 10 pravými minutami. Interval času₂ mezi poledny je 10 „pravých“ minut (10 min_P). Interval₁ ≠ Interval₂, přesto že levé strany rovnice jsou stejné.

(3)          {- 00:10} (-10 min) = 12:00_P – 12:10_S
Pokud pravé poledne nastalo ve 12:10_S, je z rovnice jasné, že střední nastalo ve 12:00_S,to je před 10 středními minutami. Interval₃ = 10 min_S.

(4)          {- 00:10} (-10 min) = 11:50_P – 12:00_S
Pokud střední poledne nastalo v 11:50_P, pravé poledne nastane ve 12:00_P, tj. za 10 pravých minut. Interval₄ = 10 min_P. Opět platí, že Interval₃ ≠ Interval₄, přesto že levé strany rovnice jsou stejné.

Příklady potvrzují, že interpretace rovnice času pro různé kombinace časů je komplikovanější než se běžně prezentuje. Obecně z levé strany rovnice není možné možné bez znalosti pravé strany říci, o jaký časový interval se jedná. Veličina E proto pro různé kombinace časů na pravé strany reprezentuje pouze rozdíl souřadnic.

Dobře definovaná funkce E (t), vztažena k hodnotám T_P (12:00:00_P, 13:00:00_P …)

Kdy bude funkce E (t) dobře definovaná? Postupujme podle konfigurace z příkladu 1. Polohy a časy budeme měřit vždy v pravé poledne ve 12:00:00_P. Grafy funkce E (t) pro spojitý čas t vytvoříme buď jako propojení jednotlivých bodů, nebo můžeme měřit i další „geometrické úhly“ poloh pravého Slunce. Půjde o okamžiky 12:00:00_P (0⁰), 13:00:00_P (15⁰), 14:00:00_P (30⁰) atd., vždy po 15⁰ definujících hodinu. Levá strana rovnice bude zde reprezentovat souřadnice středního času (odchylku od „celé“) a časový interval mezi poledny v jednotkách středního času.

Konfigurace z příkladu 1: Předpokládejme například, že se rozdíl souřadnic posune každou pravou hodinu o 1 s_S a pravý den bude celkově delší o 24 středních sekund, S_P je na obloze před S₂.

{00:10:00} = 12:00:00_P (0⁰) – 11:50:00_S,12:00:00_S nastane za 10 min_S 00 s_S, (S_P je 10:00_S před S₂)
{00:09:59} = 13:00:00_P (15⁰) – 12:50:01_S,13:00:00_S nastane za 9 min_S 59 s_S, (S_P je 09:59_S před S₂)
{00:09:58} = 14:00:00_P (30⁰) – 13:50:02_S, 14:00:00_S nastane za 9 min_S 58 s_S, (S_P je 09:58_S před S₂)
{00:09:57} = 15:00:00_P (45⁰) – 14:50:03_S, 15:00:00_S nastane za 9 min_S 57 s_S, (S_P je 09:57_S před S₂)
atd. až
{00:09:36} = 12:00:00_P (360⁰) – 11:50:24_S,12:00:00_S nastane za 9 min_S 36 s_S, (S_P je 9:36_S před S₂)

Poloha pravého Slunce na obloze se měří geometrickým úhlem (360⁰ = 24 hod), kterému odpovídá čas. Čas je mapován úhly, a to znamená, že 12:00_P je moment, kdy je pravé Slunce v meridiánu (nad hlavou), 13:00:00_P je moment pro hodinový úhel 15⁰. Zda takto definovaný čas plyne nebo neplyne rovnoměrně, můžeme zjistit jen srovnáním s jiným dějem. Dnes víme, že takto definovaný čas rovnoměrně neplyne, proto je vhodné polohy S_P udávat ve středním čase. O něm předpokládáme, že plyne rovnoměrně a až do doby mapování času dle kmitů křemíkového krystalu a později dle dějů v atomu, tu nic lepšího nebylo.

Podobné konfigurace jsou i v případě opačných poloh Sluncí z příkladu 3 (S_P je na obloze za S₂):

{-00:10:00} = 12:00:00_P (0⁰) – 12:10:00_S,12:00:00_S nastalo před 10 min_S, (S_P je 10:00_S za S₂)
{-00:10:01} = 13:00:00_P (15⁰) – 13:10:01_S,13:00:00_S nastalo před 10 min_S 1 s_S, (S_P je 10:01_S za S₂)
{-00:10:02} = 14:00:00_P (30⁰) – 14:10:02_S, 14:00:00_S nastalo před 10 min_S 2 s_S, (S_P je 10:02_S za S₂)
{-00:10:03} = 15:00:00_P (45⁰) – 15:10:03_S, 15:00:00_S nastalo před 10 min_S 3 s_S, (S_P je 10:03_S za S₂)
atd. až
{-00:10:24} = 12:00:00_P (360⁰) – 12:10:24_S,12:00:00_S nastalo před 10 min_S 24 s_S, (S_P je 10:24_S za S₂)  

Oba příklady jsou ve shodě s předchozím zjištěním, že v oblasti s delším dnem (1, 4 – 5, 8) je derivace, resp. delta E záporné pro kladná i záporná čísla.

Takto definovaná funkce E (t) bude ve všech bodech dobře a jasně definovaná. Pokud budou v tabulkách hodnoty E (t), tj. hodnoty z levé strany „rovnic času“ {00:10:00}, {00:09:59} atd., potom T_S (pro okamžik 12:00:00_P) dostaneme z rovnice E = T_P – T_S  (T_S = T_P – E). Jinak řečeno, dokážeme určit, kdy nastane „pravý čas“ v souřadnicích středního času, to znamená na našich hodinkách.

T_S (pro okamžik 12:00:00_P) = T_P (pro okamžik 12:00:00_P) – E (pro okamžik 12:00:00_P) = 12:00:00_P – {00:10:00} = 11:50:00_S. Pravé poledne nastane v 11:50 středního času (o 10 min_S dříve).

Délka pravé hodiny = (15:00:00_P -14:00:00_P)_int = (01:00:00_P)_int = (15:10:03_S – 14:10:02_S)_int =
= (01:00:01_S)_int, je to 1 hodina a 1 sekunda v jednotkách středního času (1 hod_S 1s_S).

Graf pro dobře definovanou funkci E (t), vztaženou k hodnotám T_P (12:00:00_P, …):
Osa x: reprezentuje souřadnice T_P
Osa y: na grafu zobrazuje hodnoty E v souřadnicích středního času

O takto definované funkci E je možné říci, že je dobře definovaná, protože souřadnice v rovnici můžeme geometricky měřit ke stejnému okamžiku a rozdíl je měřen ve standardním středním čase:

{00:10:00} = 12:00:00_P (0⁰) – 11:50:00_S

Okamžik 12:00:00_P (0⁰) poznáme tak, že pravé Slunce je v meridiánu, poloha středního Slunce je dána středním časem, stačí se tedy podívat na hodinky. S uvedenými vztahy se navíc dobře pracuje.

Nevhodně definovaná funkce E (t), vztažena k hodnotám T_S (12:00:00_S, …)

Polohy pravého Slunce a časy budeme tady měřit vždy v době středního poledne ve 12:00:00_S. Mezi dvěma poledny získáme další hodnoty buď interpolací, nebo přesným astronomickým měřením poloh pravého Slunce v časech (13:00_S, 14:00_S atd.). Levá strana rovnice bude potom reprezentovat souřadnice pravého času a časový interval mezi poledny v jednotkách pravého času.

Konfigurace z příkladu 2: Předpokládejme například, že 1 pravá hodina bude o 1 s_P delší než střední hodina, Slunce S_P bude na obloze před S₂. Potom 1 pravá hodina = (01:00:00_P)_int = (01:00:00_S)_int + 1 s_P a (01:00:00_S)_int = (00:59:59_P)_int. Rozdíl souřadnic se posune každou střední hodinu o 1 s_P, pravé hodiny půjdou pomaleji než střední a pravý den bude celkově delší o 24 „pravých“ sekund.

{00:10:00} = 12:10:00_P – 12:00:00_S (0⁰), 12:00:00_P nastalo před 10 min_P, (S_P je 10:00_P před S₂)
{00:09:59} = 13:09:59_P – 13:00:00_S (15⁰), 13:00:00_P nastalo před 9 min_P 59 s_P, (S_P je 09:59_P před S₂)
{00:09:58} = 14:09:58_P – 14:00:00_S (30⁰), 14:00:00_P nastalo před 9 min_P 58 s_P, (S_P je 09:58_P před S₂)
{00:09:57} = 15:09:57_P – 15:00:00_S (45⁰), 15:00:00_P nastalo před 9 min_P 57 s_P, (S_P je 09:57_P před S₂)
atd. až
{00:09:36} = 12:09:36_P -12:00:00_S (360⁰), 12:00:00_P nastalo před 9 min_P 36 s_P, (S_P je 09:36_P před S₂)

 Při konfiguraci z příkladu 4 a opačných poloh Sluncí (S_P je na obloze za S₂) platí:

{-00:10:00} = 11:50:00_P – 12:00:00_S (0⁰), 12:00:00_P nastane za 10:00_P, (S_P je 10:00_P za S₂)
{-00:10:01} = 12:49:59_P – 13:00:00_S (15⁰),13:00:00_P nastane za 10:01_P, (S_P je 10:01_P za S₂)
{-00:10:02} = 13:49:58_P – 14:00:00_S (30⁰), 14:00:00_P nastane za 10:02_P, (S_P je 10:02_P za S₂)
{-00:10:03} = 14:49:57_P – 15:00:00_S (45⁰), 15:00:00_P nastane za 10:03_P, (S_P je 10:03_P za S₂)
atd. až
{-00:10:24} = 11:49:36_P – 12:00:00_S (360⁰), 12:00:00_P nastane za 10:24_P, (S_P je 10:24_P za S₂)

I tady jsou oba příklady ve shodě s předchozím zjištěním, že v oblasti s delším dnem (1, 4 – 5, 8) je derivace, resp. delta E záporné pro kladná i záporná čísla.

Proč je to nevhodně definovaná funkce?

Ve 12:00:00_S (0⁰) můžeme změřit ve stejném okamžiku polohu pravého a středního Slunce na obloze. Geometrickým úhlům přiřadíme časové souřadnice předpisem (15⁰ je hodina,15̕‘ je 1 časová minuta a 15‘‘ je 1 časová sekunda). Hodnoty funkce E budou v tabulkách rozdíly časových souřadnic dvou Sluncí ve dvou různých soustavách. Geometrický úhel pravého Slunce definuje souřadnice pravého času, hodinky určují souřadnice středního času, tj. body 12:00:00_S (0⁰ je poloha středního Slunce).

A pokud už máme tabulky pro E, tj. hodnoty z levé strany „rovnic času“ {00:10:00}, {00:09:59} atd., potom z příslušné rovnice pro 12:00:00_S dostaneme zpětně T_P (12:00:00_S):

E = T_P – T_S, (T_P = T_S + E)
T_P (12:00:00_S) = T_S (12:00:00_S) + E (12:00:00_S) = 12:00:00_S + {00:10:00} = 12:10:00_P
Dostaneme výslednou rovnici (tentokrát už z tabulek): {00:10:00} = 12:10:00_P – 12:00:00_S (0⁰).

Jde o operace se souřadnicemi, ne s intervaly. Z informace, že 12:10:00_P nastalo v okamžiku 12:00:00_S ale nevíme, jak dlouhý byl interval od 12:00:00_P do 12:10:00_P.

Rovnice {00:10:00} = 12:10:00_P – 12:00:00_S (0⁰) je špatně zpracovatelná. My můžeme jen říci, že 12:00:00_P nastalo před 10 pravými minutami, to dokážeme určit z měřeného úhlu a jemu příslušného času, ale netušíme, jak jsou ty pravé minuty dlouhé. Měření by muselo být víc, jedno nestačí.

Intervaly mezi pravými souřadnicemi se navíc neustále (kontinuálně) mění a nedají se rozumně definovat jako seriózní 2. hodiny, dokonce ani pro krátký interval 24 hodin. Délka jednotek pravého času je totiž jako guma, kterou „někdo“ neustále natahuje a povoluje bez jasného předpisu.

Pravé Slunce se pohybuje podle tiků pravého času (ty dokonce určuje), ale my tento měnící se tep pravých hodin neznáme. O příslušný úhel se tak S_P může posunout rychle nebo pomalu. Úhlům je možné přiřadit čas podle předpisu, že 15⁰ je 1 hodina pravého času atd., ale z jednoho naměřeného úhlu nejde určit intervaly času, tj. rychlost pohybu hodinových ručiček pravého času.

U hodinek, jejichž tep neznáme, neplatí, že když máme na jedněch hodinkách 11:50₁ a na druhých 12:00₂, tak ty první se dotočí na 12:00₁ za 10 min₂. Ony se tam sice dotočí za 10 minut, ale bude to za 10 min₁, a podle druhých hodinek to může trvat jen minutu (nebo naopak hodinu). Potom 12:00₁ nastane ve 12:01₂ (nebo ve 13:00₂). Z měření úhlů v jednom okamžiku nezjistíme o chodu hodin nic.

Z uvedených důvodů je funkce E (t), pro t = 12:00:00_S, definovaná nevhodně.

Astronomické tabulky

Tabulky uvádí odchylku pravého času v okamžiku středního poledne. Hodnoty časové rovnice jsou vztažené k času 12:00 UT (Universal Time), tj. k střednímu času. Kladná hodnota znamená čas, o který pravé Slunce předbíhá střední. Záporná hodnota znamená čas, o který se pravé Slunce opožďuje za středním. Je to rovnice typu: E (12:00:00 UT) = T_P (12:00:00 UT) – T_S (12:00:00 UT).

O nevhodnosti konstruovat rovnici (např. {00:10:00} = 12:10:00_P – 12:00:00_S (0⁰)) k času t = 12:00:00_S (0⁰) pojednává celá předchozí část jako o nevhodně definované funkci E (t).

Ale co kdybychom nahradili neznámý interval 10 min_P známým intervalem 10 min_S. Jak velká chyba může vzniknout? Maximální možná chyba by měla být při maximální odchylce chodu pravého času od středního (při 30 s_S na 24 hod_S je to cca 3,5×10^-4 s/s) a při současné maximální 15 min odchylce mezi „ukazateli – ručičkami“ pravého a středního času. Výsledkem je chyba asi 0.3 s, resp. méně. Proč?

Tam, kde je maximální hodnota rozdílu mezi pravým a středním časem (maximální E), má pravý den cca 24 hod. To znamená, že pravý a střední čas jdou přibližně stejně. Tam, kde tyto dvoje hodinky jdou výrazně odlišnou rychlostí, jsou „ručičky na obou hodinách“ zas blízko, protože je to oblast nedaleko nulových a inflexních bodů. Obě tyto skutečnosti odhadovanou maximální chybu ještě výrazně zmenší. Na určení hodnoty E by se tento trik tedy mohl použít, i když „košer“ to určitě není.

Definice E (t) nepřesnou rovnicí: E = T_P* (alfa S_P) – T_S (0⁰). „Hodinovému úhlu“ pro pravé Slunce (alfa S_P) přiřadíme „chybně“ souřadnici středního času T_P* předpisem (15⁰ = 1 hod_S) místo (15⁰ = 1 hod_P).

Graf funkce E (t), konstruované k hodnotám T_S (12:00:00_S, …)
Osa x: reprezentuje souřadnice T_S  
Osa y: na grafu k hodnotám T_S zobrazuje E (= T_P – T_S) v souřadnicích středního času

Co tedy popisuje funkce E (t) = T_P (t) – T_S (t)?

E (t) popisuje rozdíl časů na dvou hodinkách, kde hodinky T_P jsou navíc „šílené“. Nejsou to “normální“ hodinky. Jejich chod se kontinuálně mění. Někdy jdou rychleji než T_S a jindy zas pomaleji. Funkce E (t) je definována rozdílem souřadnic mezi dvěma časovými soustavami T_P a T_S. Tento rozdíl je funkcí času, a tak rovnosti (např. E = 12:00:00_P – 11:50:00_S = {00:10:00}) platí vždy jen pro jeden okamžik t.  Vztahy není možné chápat jako nějaké rovnice. K levé a pravé straně nemůžeme čísla libovolně přičítat ani odečítat, rozdíl souřadnic na dvou hodinkách se v čase nezachovává, ale mění se a pro posunuté (pozdější nebo dřívější) časy platí jiné rovnosti (tj. jiné hodnoty funkce E).

Souřadnice E dovolují interpretaci jak pro pravý, tak pro střední čas (viz příklady 1 – 4) a umožňují tak různé konstrukce funkce E. Pro rovnici z předchozího odstavce to znamená, že 12:00:00_S nastane za 10 min_S a 11:50:00_P bylo před 10 min_P.

A co popisuje funkce delta E?

Funkce delta E, definovaná jako rozdíl (E (t₂) – E (t₁)), vytvoří kromě vztahu souřadnic {}, dva nové časové intervaly: Δt = (t₂ – t₁) a ΔE se zajímavou interpretací. Vzniknou vlastně dvě rovnice.

Napišme si E pro dva časy t₁ < t₂:
{E} (t₂) = T_P (t₂) – T_S (t₂)
{E} (t₁) = T_P (t₁) – T_S (t₁), potom

(1) Δ{E} = E (t₂) – E (t₁) = (T_P (t₂) – T_P (t₁)) – (T_S (t₂) – T_S (t₁))
(2) (T_P (t₂) – T_P (t₁))_int = (T_S (t₂) – T_S (t₁))_int

Δ {E} udává vzájemný posun hodin, tj. změnu souřadnic pravého času Δ T_P (t₂ – t₁) v intervalu času Δt = (t₂ – t₁), (chod hodin 1), oproti změně souřadnic Δ T_S (t₂ – t₁), za stejný časový interval. Pokud oboje hodiny jdou stejně, tak Δ {E} = 0. Nenulové Δ {E} udává rozdíl chodu dvou různých „hodin“.

Jako ukázku si můžeme vzít první dva řádky z konfigurace 1 pro „dobře definovanou funkci“ E:
{00:10:00} = 12:00:00_P (0⁰) – 11:50:00_S,12:00:00_S nastane za 10 min_S 00 s_S, (S_P je 10:00_S před S₂)
{00:09:59} = 13:00:00_P (15⁰) – 12:50:01_S,13:00:00_S nastane za 9 min_S 59 s_S, (S_P je 09:59_S před S₂)

Když odečteme vztah pro 12:00:00_P od vztahu pro 13:00:00_P dostaneme:
{- 00:00:01}_S = {01:00:00_P (15⁰)} – {01:00:01_S}

Dva členy na pravé straně reprezentují jak rozdíl souřadnic, tak interval času těmto souřadnicím příslušející, oboje se stalo za 1 pravou hodinu. Platí proto také: (01:00:00_P)_int = (01:00:01_S)_int

Levá strana je rozdíl středních souřadnic, proto výsledkem jsou souřadnice středního času.

V souladu s „dobře definovanou funkcí“ E je možné konstatovat, že ΔE < 0 znamená, že pravá hodina je delší a ΔE > 0 znamená, že pravá hodina je kratší. Pokud bude zkoumaná jednotka času delší (například den), tak platí stejné pravidlo, že pro ΔE < 0 je pravý den delší a pro ΔE > 0 je pravý den kratší. Záporná hodnota na levé straně totiž znamená, že hodnoty vlevo se zmenšují, a to je proto, že časy vpravo (ve středních souřadnicích) se zvětšují z důvodu pravého dne delšího než 24 hod_S.

Pro velmi krátký časový interval, např 1 s_P platí:
{00:00:0(1-X)}_S = 00:00:01_P (15⁰) – 00:00:0X_S, kde t₂ = např. 00:00:03_P
                                                                                      t₁ = např. 00:00:02_P

Kromě souřadnicové rovnosti platí intervalová rovnost: (00:00:01_P (15⁰))_int = (00:00:0X_S)_int
X_S udává délku 1 s_P ve středních souřadnicích
(1-X) udává jejich rozdíl také ve středních souřadnicích

Jako příklad zvláštního (zajímavého) chování rovnice je možné uvést příklad z oblasti délky v prostoru:
(600 m – 100 m) – (1 km – 0,5 km) = {499,5}

Délky v obou závorkách jsou stejně dlouhé, je to 500 m = 0,5 km. Pravá strana je sumou souřadnic. Pokud se pravá strana má blížit k nule, nebo být přímo nulová, závorky vlevo budou muset mít stejně dlouhé jednotky („hodinky jdou stejně“). Pravá strana {499,5} reprezentuje rozdíl dvou „ciferníků“.

Na jednom naměříme 500 a na druhém 0,5. Pokud naměříme jednu délku 500 jednotek prvním měřidlem v metrech a druhou délku 500 jednotek druhým měřidlem v km, rozdíl mezi délkami bude 499,5 km. To je význam pravé strany pro tento případ. U hodin je to rozdíl v délce dne měřené dvěma různými hodinkami.

Změny délky dne jako změny funkce E

Změnu délky pravého dne určuje funkce:
((T_S (t₂) – T_S (t₁)) = (– ΔE), kde časy t₁ a t₂ jsou okamžiky, kdy pravé Slunce projde 2x po sobě meridiánem.
Hodnoty (– ΔE) jsou potom odchylky od 24 hod.

Pokud platí:
(– ΔE) = 0, pravý den má 24 hod stejně jako střední,
(– ΔE) < 0, pravý den má méně než 24 hod,
(– ΔE) > 0, pravý den má víc než 24 hodin.

E a ΔE jsou funkce času a otázkou je, jak zjednodušit hledání maximálních a minimálních hodnot, tj. jak co nejrychleji najít nejdelší a nejkratší dny, případně dny o 24 hodinách. Jednou z možností je spočítat 365 hodnot pro dny v roce měřené od jednoho poledne do druhého nebo od půlnoci do půlnoci a uspořádat je. To je taky nejpřesnější, protože funkce E se spojitě mění.

Jinou možností je podívat se, kdy funkce ((T_S (t₂) – T_S (t₁)) = (– ΔE) bude nabývat lokální extrémy. Za předpokladu, že se funkce E v průběhu 24 hodin mezi okamžiky t₁ a t₂ moc nemění a můžeme si ji v rámci těchto intervalů představit jako lineární funkci (přímou úměru), bude výraz ((T_S (t₂) – T_S (t₁)) hodnotově totožný s výrazem ((T_S (t₂) – T_S (t₁)) / ( t₂ – t₁), kde ( t₂ – t₁) = 1 den. Hodnota bude udávat směrnici tečny a zároveň i rozdíl hodnot. Pro spojité změny bude možné zkoumat (– ΔE) jako derivaci E, tj. (-dE/dt), protože funkci E si můžeme nakonec představit jako propojení a vyhlazení malých úseček z jednotlivých dnů.

Bodové zkoumání průběhu křivky nemusí být absolutně totožné s porovnáním rozdílu hodnot (– ΔE), ale většinou bude postačující, jak ukazuje i následující graf. Je třeba mít na paměti ale i možné drobné odchylky těchto dvou přístupů.

Odchylka délky dne Δt₂₄ = – ∆E₂₄ = – součet změn E za 24 hodin = – Integrál (součet součinů (dE/dt)*dt) v intervalu od jednoho poledne t₁ až do následujícího poledne t₂.

Minus Integrál = – (E (t₂) – E (t₁)), tím se v kruhu dostáváme na začátek definice ((T_S (t₂) – T_S (t₁)) = (– ΔE).

Změna funkce E, resp. součet všech změn za 24 hodin, znamená přímo hodnotu času, o jakou se pravý den (reálný den se skutečným Sluncem) liší od toho středního o 24 hodinách.

Spojité a diskrétní derivace E, funkce (d/dt) E a ∆E

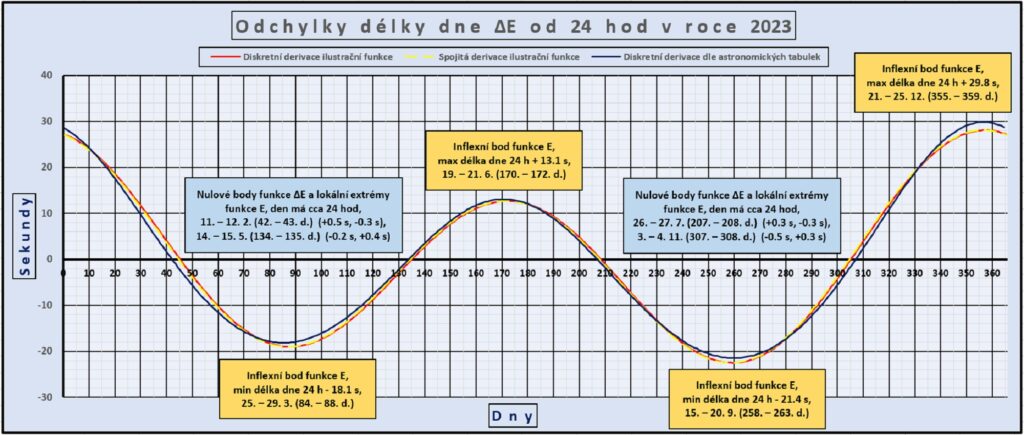
Porovnání 3 křivek derivací E

Na grafu jsou tři křivky. Jedna udává spojitou derivaci ilustrační funkce E, tj. dE/dt, jako matematickou funkci a druhá udává „diskrétní derivace“ ilustrační funkce, tj. změny ∆E za den, počítané od půlnoci do půlnoci. Třetí udává diskrétní derivace dle astronomických tabulek, měřené od jednoho poledne do druhého. Jak se dá očekávat, křivky jsou velmi podobné, ale ne absolutně totožné. Rozdíly v křivkách jsou navíc způsobené zejména velmi jednoduchým „ilustračním“ modelem křivky E, kdy ani zdaleka nejde o přesnou astronomickou křivku.

Všechny křivky jsou uvedené se znaménkem minus, protože odchylka délky dne Δt₂₄ = – ∆E₂₄. Skutečnost, že derivace funkce E udávají podobnou hodnotu jako „diskrétní derivace“ je očekávaná, derivace jsou limitní hodnoty podílů. „Diskrétní derivace“ jsou ale také určité integrály z derivací funkce E (suma součinů (dE/dt)*dt) od jednoho poledne do druhého nebo od půlnoci do půlnoci).

Z tohoto pohledu je podobnost hodnot změny délky dne za 24 hodin, tj. integrálu a „bodové“ derivace funkce E způsobena tím, že změny funkce E za 1 den nejsou velké a integrály se počítají za stejné jednotky času, na jaké se počítají derivace (tj. po dnech). Jsou to hodnoty na den a za den.

Pokud se například rychlost vlaku moc nemění, tak hodnota rychlosti 50 km/hod je číselně stejná jako vzdálenost 50 km, kterou vlak urazí za hodinu, je to číslo 50. Pokud se vzdálenost bude počítat za 2 hod nebo se rychlost bude v čase výrazně měnit, bude tam už větší číselný rozdíl.

Vztah mezi rychlostmi a časy

Skutečné a střední protiotáčení  

Měnící se otočení Země vůči Slunci můžeme popsat pomocí dodatečného úhlu „proti-otáčení“ (-ε) a následného „dotáčení“ (+ε, ε > 0) Země vůči Slunci. Definujme si úhel (-ε_S) jako průměrné proti-otočení za 24 hod a (ε_skutečné) jako reálné proti-otočení. Země se musí v průměru každý den ke Slunci „dotočit“ o cca 1⁰ (celkově o 360⁰ za rok). Otočení Země o 360⁰ reprezentuje hvězdný den, otočení o (360⁰ + ε_S) reprezentuje střední slunečný den o 24 hodinách a otočení o (360⁰ + ε_skutečné) reprezentuje pravý sluneční den (ε_skutečné je každý den trochu jíné).

t_P (doba rotace Země vůči S_P) = (360⁰ + ε_skutečné)/ω = 24 hod ± odchylka do ½ min,
t_S (doba rotace Země vůči S₂) = (360⁰ + ε_S)/ω =24 hod přesně,
kde ω = (360⁰ + ε_S)/24 hod (úhlová rychlost setrvačníkové rotace).

Platí: E = T_P – T_S = (α_P – α_S)_{na rotující Zemi} = – (α_P – α_S)_{na ekliptice}

Mapovaný čas Δt = T_P – T_S je určen funkcí E, kde E = – Δα_rel, pro úhly orientované na nebeském rovníku, znaménko bylo diskutováno dříve, 24 hod je definováno úhlem dvou po sobě následujících průchodů 2. středního Slunce meridiánem:

24 hod = – (α_S2 (t₂) – α_S2 (t₁)), střední úhel je cca 361⁰

ΔE = E (t₂) – E (t₁)= – (Δα_2rel – Δα_1rel) = – ((α_P (t₂) – α_S2 (t₂)) – (α_P (t₁) – α_S2 (t₁))) = – ((α_P (t₂) – α_P (t₁)) – (α_S2 (t₂) – α_S2 (t₁))) = – (Δα_P – (360⁰ + ε_s))

Když dvě polohy pravých Sluncí Δα_P po 24 hod odděluje úhel (360⁰ + ε_s), pak ΔE = 0 a pravý den má přesně 24 hod. Nenulová odchylka Δα_P od (360⁰ + ε_s) určuje odchylku od středního dne (od 24 hod) měřenou ve stupních (15⁰ je 1 hod). Určující není relativní poloha Sluncí, ale její změna.

Čas v tomto i v jiných případech je určen vždy změnou, a zde je změna délky dne určena změnou relativní polohy Sluncí, tzn. funkcí ∆E.

Změny funkce E udávají rychlosti i časy zároveň

V předchozích textech byla změna funkce E někdy rychlost a jindy čas (změna délky dne). To je trochu zvláštní. Jak to, že rychlost může být současně i časem a udávat změnu délky dne? Je to proto, že rychlost je změna dráhy (úhlu) za čas a dráha nebo úhel zde reprezentují mapovaný čas (pravý, střední nebo jejich vzájemný rozdíl). Přírůstek úhlu při mapování času definuje plynoucí čas.

Změny časových rozdílů E, tj. ΔE, udávají odchylky plynutí časových souřadnic u dvou systémů měření: dle pravého Slunce a dle středního: ((α_P (t₂) – α_P (t₁)) – (α_S2 (t₂) – α_S2 (t₁))). Stejný, ale jinak přepsaný výraz znamená změnu relativní rychlosti ((α_P (t₂) – α_S2 (t₂)) – (α_P (t₁) – α_S2 (t₁))) za 24 hod. Takže odchylka délky pravého dne je rovna změně relativní rychlosti za stejných 24 hod.

Bodové změny reprezentují průběh relativní úhlové rychlosti a zároveň malé bodové změny pravého času vůči střednímu. Integrály (součty součinů za 24 hodin), tj. diskrétní hodnoty ΔE jsou velké (intervalové) změny délky dne i relativní úhlové rychlosti.

Předchozí graf pro odchylky délky dne od 24 hod je proto i grafem průběhu relativní rychlosti pravého Slunce vůči střednímu. V nulových bodech tohoto grafu je odchylka plynutí pravého času vůči střednímu nulová, den má 24 hod a nule je rovna i relativní rychlost Sluncí.

Zdroje dat

Zdroj dat pro perihélium a afélium:
https://www.timeanddate.com/astronomy/perihelion-aphelion-solstice.html

Zdroj dat pro roční období:
https://en.wikipedia.org/wiki/Solstice

Zdroj astronomických dat pro hodnoty „rovnice času“:
https://kalendar.beda.cz/hodnoty-casove-rovnice