Teorie variabilního mapování času

Článek sumarizuje matematické poznatky získané při konstrukci časových systémů v letech 2018 – 2023. Teorie variabilního mapování času řeší hlavní problém strojového pásmového času. Tím je nesoulad mezi biologickým cyklem člověka svázaným se světlem a tmou (zejména s východy Slunce), a strojovým pásmovým časem, který je svázán s denním cyklem Slunce (se středním slunečním dnem), ale nerespektuje roční cyklus, tj. sezónní změny východů Slunce, zejména v oblasti mírného pásma mezi obratníky a polárními kruhy. Strojový čas není z tohoto důvodu pro člověka vhodný. Variabilní mapování přirozeného slunečního času definuje nový systém měření, který dokáže roční cyklus Slunce zohlednit.

Bezprostředně související články

Administrace přirozeného slunečního času
Symmetrical natural solar time tables
Symmetrical natural solar time graphs
Symmetrical natural solar time tables for the year 2020

Obsah teorie variabilního mapování času

1. Co je přirozený sluneční čas?
   1.1 Které body slunečního cyklu jsou pro člověka významné?
   1.2 Které body slunečního cyklu nejsou pro člověka významné?
   1.3 Které body slunečního cyklu jsou významné pro vědu a techniku?
2. Technický přirozený sluneční čas
   2.1 Základní pojmy a nastavení jednotek
   2.2 Variabilní mapování času – princip měření
   2.3 Nastavení bodů obratu
   2.4 Běžný a přestupný rok jako proměnná časového cyklu
   2.5 Systém značení a první pravidla pro nové jednotky času
3. Asymetrický přirozený sluneční čas (ANST)
   3.1 Asymetrický přirozený sluneční čas ANST₇₃
   3.2 Asymetrický přirozený sluneční čas ANST₉₁₁₅
   3.3 Přepočet časových souřadnic obecně
   3.4 Základní rovnice pro konstrukci ANST v běžném roce (365 dní)
   3.5 Vložení jednoho dne do ročního cyklu ANST
   3.6 Základní rovnice pro konstrukci ANST v přestupném roce (366 dní)
   3.7 Některé vybrané vlastnosti asymetrického času ANST₇₃
   3.8 Paradox ANST hodin
4. Symetrický přirozený sluneční čas (SNST)
   4.1 Symetrický přirozený sluneční čas SNST₇₃
   4.2 Symetrický přirozený sluneční čas SNST₉₁₁₅
   4.3 Přepočet časových souřadnic obecně
   4.4 Základní rovnice pro konstrukci SNST
   4.5 Vložení jednoho dne do ročního cyklu SNST
   4.6 Základní rovnice pro konstrukci SNST v přestupném roce (366 dní)
   4.7 Sčítání a odečítání u SNST hodin graficky
   4.8 Konstantní posuny časového systému SNST značené jako (-)
5. Vlastnosti a charakteristiky časových systémů
   5.1 Odchylky mezi symetrickými a asymetrickými sekundami
   5.2 Shoda časů a maximální odchylky mezi SNST₇₃ a ANST₇₃
   5.3 Shoda časů a maximální odchylky mezi SNST₉₁₁₅ a ANST₉₁₁₅
   5.4 Symetrie a asymetrie časových systémů
   5.5 Souřadné soustavy času
   5.6 Netransformovatelnost symetrických a asymetrických systémů
   5.7 Celočíselnost řešení pro běžný a přestupný rok
6. Další posuny času a vyrovnávání rozdílů mezi UTC a UT1
   6.1 Používané značky, zkratky a úvod do problematiky
   6.2 Přestupná sekunda
   6.3 Co je zdrojem nesouladu mezi UTC a UT1
   6.4 Přestupná sekunda a SNST₇₃ nebo SNST₉₁₁₅
   6.5 Jaký nejmenší čas je možné vkládat do SNST₇₃ a SNST₉₁₁₅?
   6.6 Vkládání a vynechávání časových intervalů v rámci SNST obecně
   6.7 Pružnost času
   6.8 Celočíselnost a vkládání časových intervalů do ročního cyklu
   • 6.8.1 Vložení nebo odebrání 1 sekundy
     6.8.2 Výsledky výpočtů pro vložení nebo odebrání 1 sekundy
     6.8.3 Jiné (menší) vložené intervaly a celočíselnost
     6.8.4 Výsledky výpočtů pro vložení nebo odebrání 0,1 s

1. Co je přirozený sluneční čas?

Za přirozený sluneční čas lidé v minulosti považovali různé časové systémy. Především lokální sluneční čas nebo později pásmový čas. V čem spočívá podstata skutečné opravdové „přirozenosti“?

Přirozený sluneční čas je čas určený slunečním cyklem a není deformován (pokřiven) žádnou nepřirozenou definicí, na které by se lidé z moci úřední nebo z moci panovnické dohodli. Je to reálný čas taktující cyklus života, který funguje v přírodě po tisíce let a nepotřebuje žádné hodinky ani umělé definice. Stačí popsat denní cyklus Slunce a do popisu zahrnout i jeho změny v průběhu roku.

Každý den začíná svítáním, pak nastává východ Slunce a celá příroda se probouzí, později s přibývajícím časem Slunce stoupá po obloze stále výš a výš, kulminuje v nejvyšším bodě své dráhy a následně zas klesá, aby nakonec pozdě večer na rozhraní dne a noci za obzorem zapadlo a po soumraku nastala noc. Právě tento časový cyklus vnímá celá příroda jako přirozený.

Je třeba se zamyslet, zda astronomy tolik oslavované poledne je skutečně tak důležité, a zda nejsou v životě lidí mnohem důležitější jiné body slunečního cyklu. A ukazuje se, že ano. Poledne je třeba smést z oltáře.

1.1 Které body slunečního cyklu jsou pro člověka významné?

Prvým významným bodem pro živou přírodu je moment, kdy noc ztrácí na síle, začíná svítání a po nějakých 30 až 40 minutách vychází Slunce. To pozná každé zvířátko i každá rostlina.

Druhým významným bodem je západ Slunce a následný soumrak, kdy přichází noc. Čas, který se řídí podle těchto důležitých a významných bodů je možné označit za přirozený sluneční čas a moderní měření času by se mu mělo alespoň v rámci nějakého „technického kompromisu“ co nejvíce přiblížit.

Významné body pro živou přírodu jsou východ a západ Slunce.

1.2 Které body slunečního cyklu nejsou pro člověka významné?

Poledne není pro živou přírodu nijak zvlášť významný bod. Zvířata ani rostliny poledne jako exaktní bod kulminace Slunce neregistrují, významný je hlavně růst teploty prostředí, ale ta roste s jistým zpožděním až v odpoledních hodinách a nekulminuje ve 12:00, takže zvířata vnímají spíše kulminaci odpoledního horka než nějaké pravé poledne. Přesto, že existuje přímá souvislost mezi kulminací Slunce na obloze a odpoledním horkem vrcholícím kolem druhé až čtvrté hodiny odpolední, pravé poledne jako bod má smysl spíš v teorii než v realitě.

Poledne (jako exaktní časový bod 12:00:00) není pro živou přírodu vůbec významné, důležitá je spíš kulminace odpoledního tepla.

Půlnoc je ještě daleko bezvýznamnější, tu neregistruje už vůbec nikdo. Půlnoc je naprosto umělý matematický bod, který není bez měření a „technických pomůcek“ vlastně vůbec „rozeznatelný“. Těžko by někdo mohl uprostřed noci, jen na základě svého vnitřního pocitu nebo pohledem po krajině, prohlásit nějaký časový okamžik za půlnoc. Z tohoto důvodu je možné říci, že půlnoc jako exaktní časový bod 24:00:00 je pro živou přírodu zcela bezcenná.

Půlnoc (jako exaktní časový bod 24:00:00) je pro živou přírodu zcela bezcenná.

1.3 Které body slunečního cyklu jsou významné pro vědu a techniku?

Současné měření času, definované na základě intervalu od jednoho poledne do druhého, svoji logiku má, protože na začátku bylo potřebné hledat nějaké stabilní periodické děje, a právě tato „mezi-polední“ doba takovým relativně stabilním periodickým dějem je.

Kdyby lidé měřili čas od jednoho východu Slunce do druhého, časové intervaly by se nikdy nemohly správně nastavit a řádné měření času by možná nikdy nevzniklo. Od našich předků to bylo velmi moudré rozhodnutí měřit čas právě takto a ne jinak. Věda tak mohla definovat například střední sluneční den jako abstraktní veličinu vhodnou k dalším teoretickým nebo experimentálním účelům.

V minulosti bylo možné právě na základě těchto měření nastavit délku sekundy jako jednotky času a přesto, že sekunda dnes už není definována jako 1/86 400 část dne, původně tak vznikla. Dnešní definice je už mnohem přesnější a umožňuje měřit dokonce i změny a nepravidelnosti rotace Země.  

Poledne je proto významným bodem pro vědu, časový interval mezi následujícími kulminacemi Slunce na obloze trvá cca 24 hodin a je periodickým dějem vhodným k měření.

Půlnoc je v cyklu dne opakem poledne a v teorii má také svoje místo. V moderním světě definuje například začátek dne, týdne, měsíce i nového roku. Zcela nepřirozený a odlidštěný bod, kdy jsou lidské aktivity významně utlumené, je vhodný na technické oddělení dvou dnů v rámci kalendářního systému.

Dnešní doba je naštěstí už někde jinde, věda a technika zvládají měření času s vysokou přesností, sekunda je dnes taktována atomovými hodinami, a proto se můžeme posunout o krok dál s vědomím, že bez dlouhé a náročné cesty, kterou technika v minulosti urazila, by následující krok nebyl možný.

Významné body pro vědu jsou poledne (12:00:00) a půlnoc (24:00:00).

2. Technický přirozený sluneční čas

2.1 Základní pojmy a nastavení jednotek

Významné body pro živou přírodu jsou východ a západ Slunce, ale protože měření času musí splňovat také podmínku smysluplnosti měření fyzikální veličiny a nemůžeme měřit „od buka do buka“ jako Jánošík, je třeba zavést pojem „technický přirozený sluneční čas“, který se v rámci kompromisu snaží zohlednit jak ideální přirozený sluneční čas, tak rozumné měření fyzikální veličiny, včetně zakomponování „globalizace“ života lidí v moderní době. Není možné, aby měl každý člověk nějaký svůj osobní (byť ideální) čas. Synchronizace časů ve společnosti je nutnost.

„Technický přirozený sluneční čas“ je z hlediska jednotek a taktování hodin odvozen od UTC a jednotek SI. Na tomto v současnosti nejmodernějším strojovém času jsou vytvořené nové technické křivky, které se v rámci možností snaží modelovat ideální přirozený sluneční čas. To jasně vymezuje potřebné mantinely a trochu uměleckou až bohémskou definici přirozeného slunečního času vrací zpět k technice, fyzice a potřebné přesnosti.

Časový systém UTC (Coordinated Universal Time) je čas měřený na základě atomových hodin a korigovaný dle UT (Universal Time). Je to mezinárodní standard pro měření času. Podobně jako GMT používá také časová pásma (UTC+1, UTC+2…) a v běžné mluvě se s ním někdy zaměňuje.

Přirozený sluneční čas, popsaný na předchozích stranách, je ideál a vzor. Pokud je v dalším textu tento pojem používán ve výpočtech, rovnicích a tabulkách, jedná se vždy o technický přirozený sluneční čas. Důvodem je stručnost vyjadřování.

Strojový (robotický) čas je současný časový systém definovaný na základě stále stejných po sobě následujících intervalů času, jejichž délka se nemění. Strojový čas je vhodný na řízení chodu strojů a přístrojů, a je využívaný ve vědě a technice, protože umožňuje jednoduše srovnatelná měření a tvorbu fyzikálních zákonů. Slovo „robotický“ zde není používáno jako technický pojem (vztaženo k robotům), ale ve smyslu „uměleckém“ jako protiklad k něčemu živému, pružnému a elegantnímu, tzn. jako těžkopádný, nepružný a neživý. Příkladem je tančící robot vykonávající těžkopádné a nepřirozené pohyby v protikladu k tanečnici s ladnými a harmonickými pohyby. 

Pro úpravu strojového času na přirozený sluneční čas, vhodný k celoročnímu používání, stačí prodloužit nebo zkrátit každou sekundu o malý zlomek času v řádu 10^-4 sekundy. Od zimního do letního slunovratu hodiny půjdou trochu rychleji, nejlépe o 1 s/hod (nová sekunda na hodinách bude tedy zkrácená) a od letního do zimního slunovratu hodiny půjdou o stejnou hodnotu pomaleji (nová sekunda na hodinách bude delší).

Hodiny na jaře tikají o 2,8*10^-4 sekundy rychleji a na podzim o stejnou hodnotu pomaleji.

Takto nepatrná a v reálném životě nepozorovatelná změna znamená 24 sekund za den a za půl roku do slunovratu je to přesně 73 min. V případě urychlení (zpomalení) hodin o 1,25 s/hod je to 30 sekund za den a za půl roku 91 minut a 15 sekund. Vzhledem k tomu, že čas na hodinách se o stejnou hodnotu první půlrok natáhne a druhý půlrok zkrátí, vždy jeden den v roce, v době zimního slunovratu, se oba časy (starý a nový) setkají s naprostou přesností.

2.2 Variabilní mapování času – princip měření

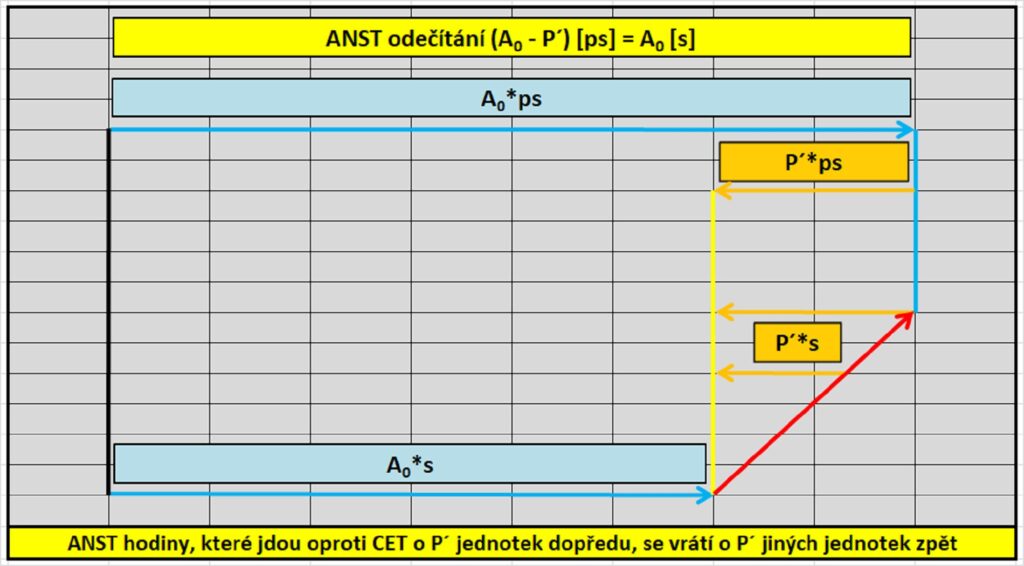
Jak je vidět z obrázku, u současného měření se hodnota měřené veličiny mění jako násobek základní jednotky a plyne stále stejně až do nekonečna. Při novém způsobu měření dochází k periodické změně časové jednotky (zde po půl roce) tak, aby se na ukazatel času navázané činnosti a aktivity lidí spojitě přesouvaly v čase jedním nebo druhým směrem.

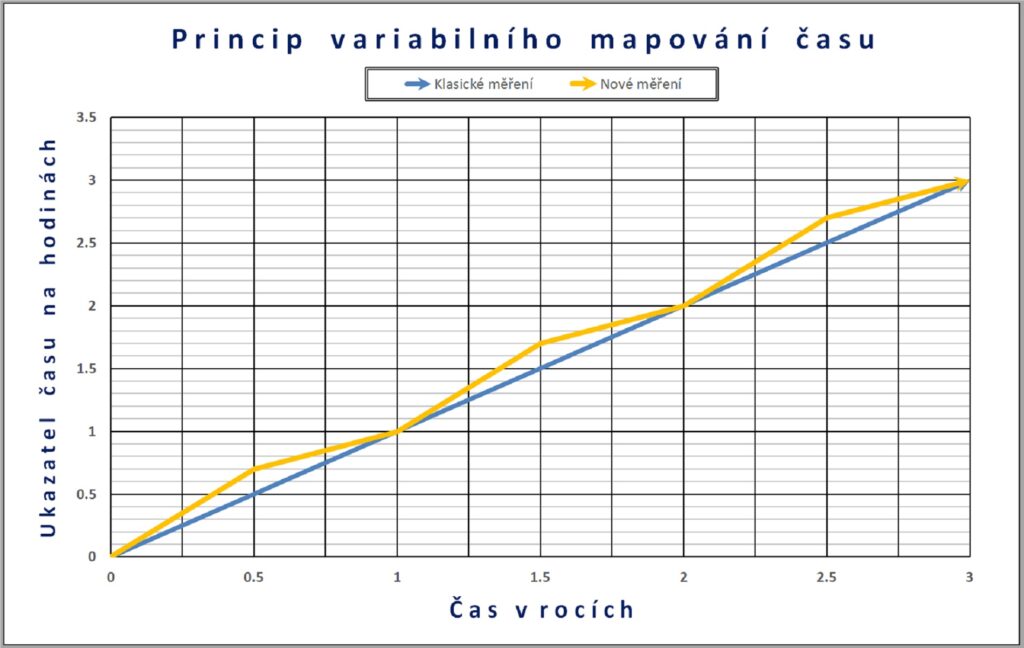
Obrázek ukazuje pouze princip, ne velikost odchylky. Aby odchylka žluté čáry od modré na svislé ose byla 1 mm, musela by být vodorovná osa dlouhá 3,6 metru, a to znamená, že i na hodně velkém grafu obě čáry splývají jako naprosto totožné. Proto by „utajenou“ záměnu hodin u všech lidí najednou jen málokdo zaregistroval.

Ve zdokonalené variantě může nové časové vlákno to hlavní dvourozměrně „ovinout“, pokračovat z plusových hodnot až do mínusových a posouvat čas i v zimě. Průběh občanského času (osa y) je na grafu zobrazen neperiodicky, tj. jako suma všech hodnot.

2.3 Nastavení bodů obratu

Setkání dvou časových systémů jako svátek a oslava času – the show must go on

Východiskové body obratu, vhodné pro změnu chodu hodin, jsou zimní a letní slunovrat. Letní slunovrat se neslaví, ani se mu nevěnuje nějaká zvláštní pozornost, svátek je tedy „neobsazený“. V zimě hned po slunovratu přichází Vánoce, proto se den zimního slunovratu na zavádění nových zvyků nehodí, ale po Vánocích následuje konec starého a začátek nového roku, a nemůže být nic vhodnějšího a lepšího než tato světská událost, spojená s kultovním sledováním tikajících hodin.

Tradice s megalomanským Silvestrem, kterou provází divoké bujaré oslavy a ohňostroje po celém světě, je pro start nového času jako stvořena, proto může právě na Silvestra o půlnoci pravidelné setkávání a rozcházení obou časů začít. Náměstí a dvoje hodiny, které se přesně o půlnoci sejdou a hned zas rozejdou, mohou znamenat příjemné zpestření života i kontrolu času zároveň.

Astronomické argumenty

K pokračování silvestrovské show nepřímo nabádá i astronomie. Při prvním pohledu je ideálním bodem k obratu a nastavení počátku nového měření den zimního slunovratu. Při bližším zkoumání ale objevujeme nečekanou souvislost. Navzdory očekávání, že hned na druhý den po slunovratu bude Slunce vycházet každý den dřív a dřív zjišťujeme, že ještě déle než týden Slunce vychází stále později, i když se den už prodlužuje.

Vše se otočí až po Novém roce. Obrat v den slunovratu by znamenal, že svítání kolem Vánoc a Nového roku by se opožďovalo ještě víc. To rozhodně není cílem konstrukce technického přirozeného slunečního času. Proto je i z astronomického hlediska vhodné obrat posunout až na konec kalendářního roku. The show must go on.

Hledisko administrativní

Z administrativního hlediska konec roku znamená hodnocení všech důležitých aktivit za uplynulý rok. Závěr roku je spojen s bilancováním soukromého i pracovního života. Ve firmách se hodnotí lidé, výroba i finance, např. množství vyrobených výrobků, roční obrat, příjmy a výdaje, zisk, úspory nebo daně. Na úřadech provádí kalkulace různých ukazatelů a parametrů jednotlivých činností a projektů, a vyhodnocení provádí také školy, nemocnice, pojišťovny nebo vědecko-výzkumné organizace. Bilancují lidé, firmy i stát. Nějaká výrazná a zcela zásadní změna by mohla pravidelný chod těchto důležitých činností vážně narušit a z tohoto důvodu je prakticky nemyslitelná.

Začátek a konec nového kalendářního a časového systému musí být v souladu se současným koncem kalendářního roku. Navržené systémy to splňují v některých případech s absolutní přesností a k průsečíku časů dochází přesně o půlnoci. V jiných případech, kdy časové systémy využívají také optimalizaci konstantním časovým posunem, aby modelovaly nejen „letní“, ale také „zimní“ čas, se Silvestr může lišit maximálně o desítky minut (vždy je to méně než 1 hodina). Bilancování na konci roku proto může nerušeně pokračovat dál.

2.4 Běžný a přestupný rok jako proměnná časového cyklu

Při nastavováním bodů obratu bude nutné v konstrukci časových systémů zohlednit ještě skutečnost, že délka roku není v kalendářních a administrativních jednotkách stále stejná.

Každý čtvrtý rok má 366 dní místo obvyklých 365 dní, a to v případě, že letopočet je dělitelný čtyřma (s výjimkami každých sto let). Den navíc se vkládá do měsíce únor jako 29. den v pořadí. V přestupném roce tedy únor nemá 28, ale 29 dní. Proč musíme vkládat každé čtyři roky 1 den? Protože oběh Země kolem Slunce netrvá přesně 365 dní, ale přibližně 365,25 dne. Bylo by docela překvapivé, kdyby oběh Země kolem Slunce trval přesně celočíselný násobek dnů, tj. otočení Země kolem své osy. Tyto děje spolu totiž nesouvisí.

Při každém oběhu Země kolem Slunce (měřeném podle kalendářního roku o 365 dnech) Země na oběžné dráze zaostane o cca ¼ dne a tomu odpovídající vzdálenost (365 dní < skutečná doba oběhu Země 365,24219 dne). V takovém případě se roční období v kalendáři posouvají na pozdější datum. Za 40 let se opozdí asi o 10 dní (9,7). Po staletích by to znamenalo, že léto by bylo v prosinci a zima v červnu (posun o půl roku by nastal za 754 let). Proto Julius Caesar nařídil vkládání přestupného dne každé 4 roky už v roce 45 př. n. l. a zavedl tak na mnoho staletí juliánský kalendář.

Protože skutečná délka oběhu Země kolem Slunce není 365,25 dne, ale 365,24219 dne, roční období se i nadále posouvala, i když už pomaleji, cca 1 den za 128 let, a pro změnu zas opačným směrem, tj. na dřívější období (365,25 dne > 365,24219 dne). Proto zavedl papež Gregor (Řehoř) XIII. v roce 1582 ještě další korekci vztaženou na přesnější a realitě bližší číslo 365,2425.

Tato korekce říká, že po každých 100 letech žádný přestupný rok nebude (0,24*100 = 24 dní, ne 25), ale po 400 letech ano (400*0,0025 = 1 den). Tento kalendář používáme dodnes jako tzv. gregoriánský kalendář. Ty „drobné“ mezi 365,2425 a 365,24219 se časem nasčítají a budou se muset jednoho dne (za 3226 let) opět řešit.

Nové pravidlo o přestupných dnech ale nestačilo. V roce 325 byl totiž v Nikaji stanoven jako den jarní rovnodennosti a začátek jara 21. březen v souvislosti s výpočty data pro Velikonoce. Velikonoční svátky nastávají první neděli po prvním úplňku po 21. březnu. Jarní den se posouval každých 128 let o 1 den dříve a do roku 1582 tento rozdíl (s juliánským kalendářem) narostl na 10 dní, a to bylo dlouhodobě neakceptovatelné (v současnosti je to už 13 dní). Z tohoto důvodu bylo potřebné, kromě nového pravidla pro vkládání přestupných dní, posunout i datum a 10 dnů z kalendáře vynechat.

Tak se nový gregoriánský kalendář posunul o deset dní dál. Juliánský kalendář se tak oproti gregoriánskému skokově zpozdil, a protože juliánský rok (365,25 dne) je delší než gregoriánský (365,2425 dne), zpožďování pokračuje dál. U juliánského kalendáře nastává letos jarní rovnodennost „už“ 7. března místo 20. března 2023. Proto byla říjnová revoluce v roce 1917 v Rusku podle dnešního gregoriánského kalendáře 7. listopadu, ale podle juliánského, který se opožďuje o 13 dní, „už“ 25. října. Opoždění kalendáře nebo času znamená, že událost nastává zdánlivě dříve.

Nové časové systémy proto musí být schopné vkládat každé čtyři roky do konstrukce systému měření časový interval 24 hod = 86 400 s a synchronizovat ho s dvěma odlišně měřenými intervaly času, jeden bude v krátkých (jarních) a druhý v dlouhých (podzimních) sekundách.

O přestupném roce
https://kalendar.beda.cz/proc-existuji-prestupne-roky

2.5 Systém značení a první pravidla pro nové jednotky času

Zkratky a pravidla pro jednotky

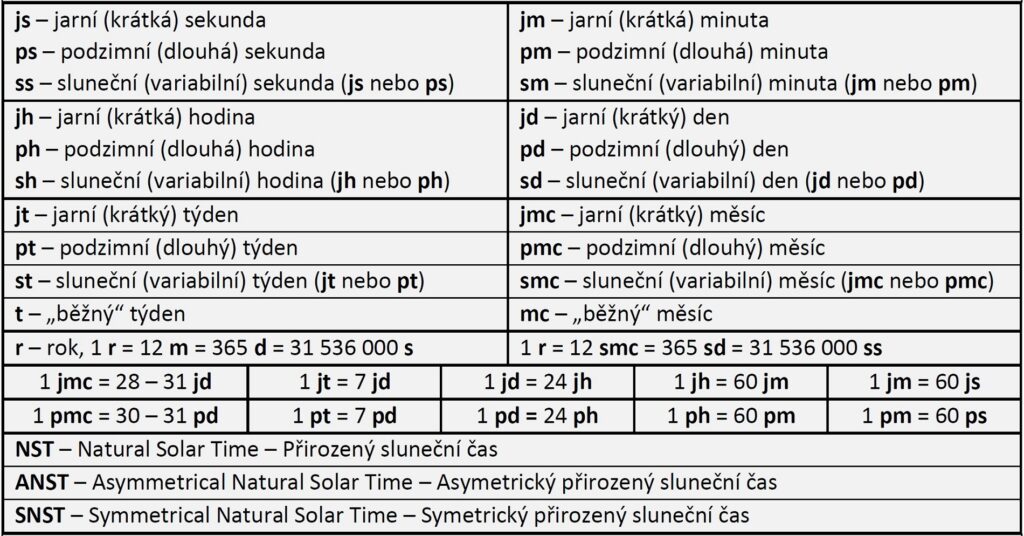
Slovo „jarní“ tu znamená období od zimního slunovratu do letního podobně jako slovo „podzimní“ znamená období od letního slunovratu do zimního. Časový interval není slunovraty ohraničen úplně přesně, protože je tvořen obraty, které nejsou se slunovraty absolutně totožné. Jsou posunuté asi o týden. „Sluneční“ je původně používané slovo pro jarní a podzimní sekundy, které říká, že časové jednotky souvisí se Sluncem a snahou zachovat co největší soulad se slunečním cyklem. Oproti současným jednotkám, které maximálně optimalizují soulad s denním cyklem Slunce, nové jednotky optimalizují soulad s ročním cyklem.

Výrazy „dlouhý“, „krátký“ a „variabilní“ jsou neutrálnější a nemají žádnou vazbu na roční období. Jsou vázané pouze na fyzikální délku časové jednotky.

Vzhledem k tomu, že takto koncipované časové a kalendářní jednotky mají „správní“ charakter, týkají se správy a řízení chodu společnosti, výraz „variabilní“ je možné nahradit i „civilnějším“ slovem „administrativní, občanská“ sekunda (minuta, hodina, den, týden a měsíc).

3. Asymetrický přirozený sluneční čas (ANST)

Výpočet slunečních (variabilních) jednotek času je možné nastavit buď symetricky, nebo asymetricky. Jako první uvedeme asymetrický NST. V úvahách vznikl jako první. Pokud začneme uvažovat o posunu času, v první fázi nás pravděpodobně vždy napadne asymetrický NST. Přesto, že se intuitivně snažíme o symetrickou konstrukci, výsledek je asymetrický. 

Chceme, aby hodiny šly půl roku rychleji, proto ke každé hodině chodu běžných hodin přidáme (například) jednu sekundu. Potom půl roku každou hodinu stejnou sekundu zas ubíráme, aby hodiny šly pomaleji a vrátily se zpět. Synchronizujeme to vždy s celou hodinou běžných hodin, které intuitivně považujeme za ty „správné“ (referenční). Výsledkem je asymetrický NST. Proč?

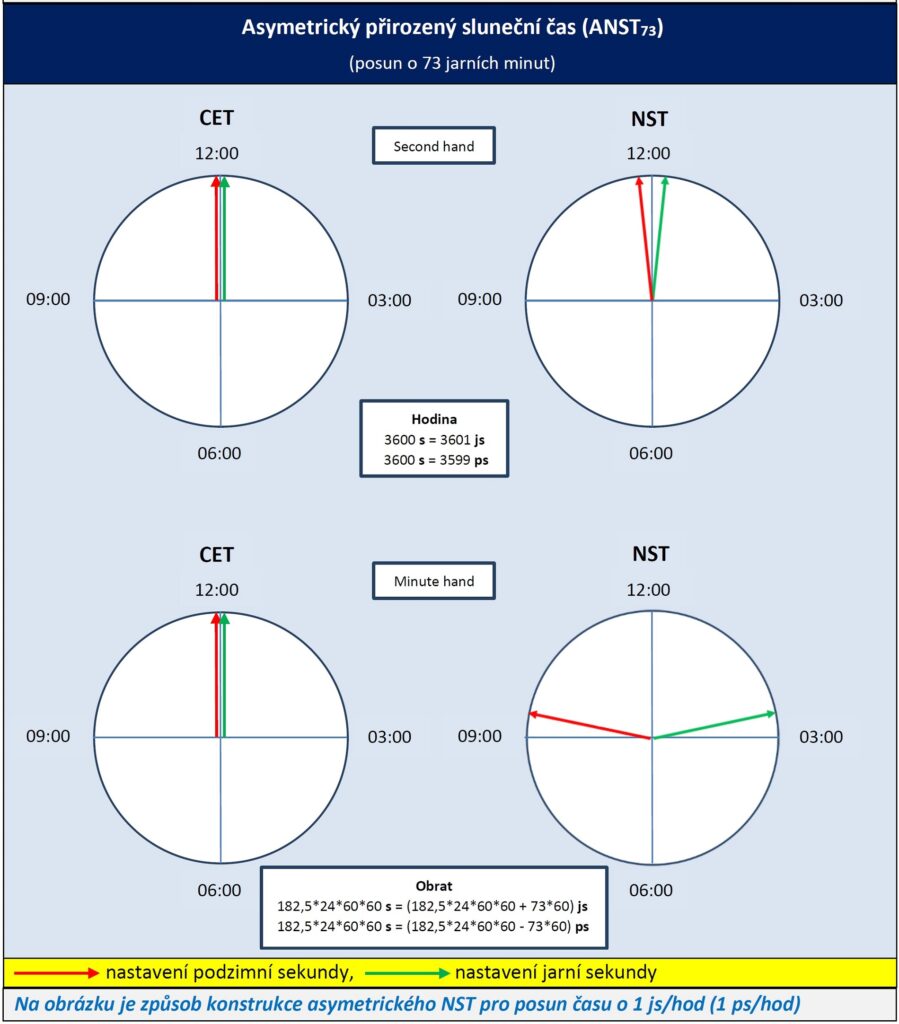
Pokud považujeme původní hodiny za správné a referenční (jak jinak, ty nové jsou přece „divné“), logicky nastavíme obrat na polovinu roku: 183. den ve 12:00 dle CET, to je 183. den ve 13:13 dle ANST. To má za následek, že počet jarních a podzimních sekund není stejný a důsledkem toho ani jejich „prodloužení“ nebo „zkrácení“ vůči „běžné“ sekundě není stejné, je asymetrické.

3.1 Asymetrický přirozený sluneční čas ANST₇₃

Parametry rovnic

A – počet sekund od začátku roku do daného okamžiku, ale maximálně do bodu obratu [s]
B – počet sekund od bodu obratu do daného okamžiku, ale maximálně do konce roku [s]
C = A + B – celkový počet sekund od začátku roku do daného okamžiku [s]

A´ – počet js od začátku roku do daného okamžiku, ale maximálně do bodu obratu [js]
B´ – počet ps od bodu obratu do daného okamžiku, ale maximálně do konce roku [ps]
C´ = A´ + B´ – celkový počet slunečních sekund od začátku roku do daného okamžiku [ss]

Přepočet CET → ANST₇₃
ANST₇₃ [ss] = A´ + B´ = A/(js [s]) + B/(ps [s]) = A * 3601/3600 + B * 3599/3600 = C + (A – B)/3600

Přepočet ANST₇₃ → CET
CET [s] = A + B = A´/(s [js]) + B´/(s [ps]) = A´ * 3600/3601 + B´ * 3600/3599 = C´ + (B´/3599 – A´/3601)

Důležité: Při výpočtech se ukázala jako nejlepší „nepuristická formulace rovnic“ s maximem „bezrozměrných“ parametrů, které fungují jen jako „čísla“ a s minimem explicitních časových jednotek. Rovnice popisují jen časové jednotky: s, js_s, ps_s, ss_s, js_a, ps_a, ss_a. Jde o „násobky“ sekundy, kde násobek není tisíc ani milion, ale velmi malý zlomek: 3599/3600 nebo 3600/3601 atd. Puristické uvádění všech jednotek v rovnicích u všech zlomků se ukázalo jako možné (pak je nutné dosazovat jednotky i ke všem číslům: 3600 s, 3601 js, 3599 ps), ale kontraproduktivní a neužitečné.

3.2 Asymetrický přirozený sluneční čas ANST₉₁₁₅

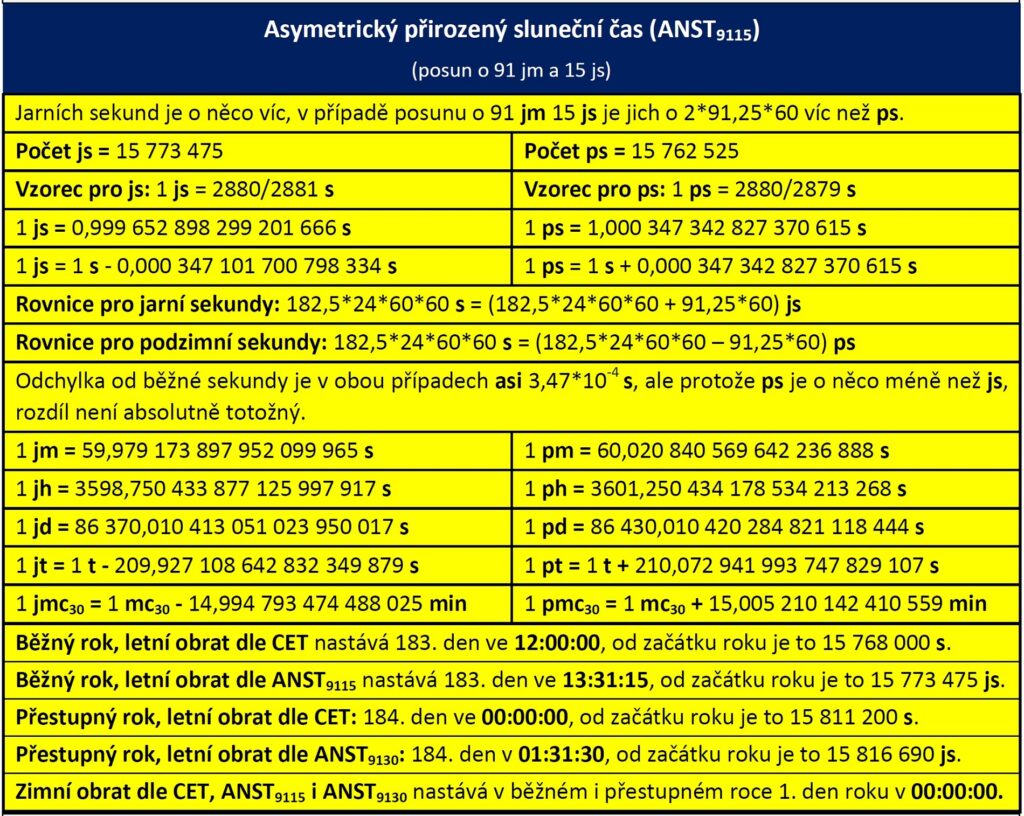
Parametry rovnic

A – počet sekund od začátku roku do daného okamžiku, ale maximálně do bodu obratu [s]
B – počet sekund od bodu obratu do daného okamžiku, ale maximálně do konce roku [s]
C = A + B – celkový počet sekund od začátku roku do daného okamžiku [s]

A´ – počet js od začátku roku do daného okamžiku, ale maximálně do bodu obratu [js]
B´ – počet ps od bodu obratu do daného okamžiku, ale maximálně do konce roku [ps]
C´ = A´ + B´ – celkový počet slunečních sekund od začátku roku do daného okamžiku [ss]

Přepočet CET → ANST₉₁₁₅
ANST₉₁₁₅ [ss] = A´ + B´ = A/(js [s]) + B/(ps [s]) = A * 2881/2880 + B * 2879/2880 = C + (A – B)/2880

Přepočet ANST₉₁₁₅ → CET
CET [s] = A + B = A´/(s [js]) + B´/(s [ps]) = A´ * 2880/2881 + B´ * 2880/2879 = C´ + (B´/2879 – A´/2881)

3.3 Přepočet časových souřadnic obecně    

Přepočet CET → ANST
ANST [ss] = C´ = A´ + B´ = A/(js [s]) + B/(ps [s]) = A*(k+1)/k + B*(k-1)/k = C + (A – B)/k

Přepočet ANST → CET
CET [s] = C = A + B = A´/(s [js]) + B´/(s [ps]) = A´*k/(k+1) + B´* k/(k-1) = C´ + (B´/(k-1) – A´/(k+1))

Platí: 1 js = k/(k+1) [s]
          1 ps = k/(k-1) [s]

Z pohledu CET jednotek času se jedná o k-cyklus, z pohledu ANST jednotek je to buď (k+1)-cyklus pro js nebo (k-1)-cyklus pro ps.

Dvě rovnice a jejich výklad

C´ = C + (A – B)/k
C = C´ + (B´/(k-1) – A´/(k+1))

Tyto rovnice jsou jen algebraickou úpravou definičních vztahů pro převod souřadnic mezi časovými systémy, ale jejich zajímavý algebraický tvar nutí k zamyšlení nad významem těchto upravených rovnic.

Rovnice C´ = C + (A – B)/k

Co tato rovnice znamená? Jak je vidět z úvodního obrázku, kde se nastavuje js, ps a s, na každý uzavřený k-cyklus v CET, dostaneme v ANST co do počtu jednotek jednu časovou jednotku (1 js) navíc, nebo o jednu jednotku (1 ps) méně. Interval A sekund bude obsahovat (A/k) k-cyklů, tj. (A/k) js navíc oproti počtu sekund v intervalu A (kterému odpovídá v ANST příslušný počet A js + přírůstek).

Počet js: A´ = (A + A/k)

V intervalu B bude na každý uzavřený k-cyklus (v CET) v systému ANST naopak o 1 ps méně. Interval B bude obsahovat (B/k) cyklů, tj. o (B/k) ps méně, než je počet sekund v intervalu B (kterému odpovídá i příslušný počet B ps – úbytek).

Počet ps: B´ = (B – B/k)

Rovnice C = C´ + (B´/(k-1) – A´/(k+1))

I zde je nutné vyjít z úvodního obrázku pro seřízení všech časových jednotek. Po každém (k+1)-cyklu odehrávajícím se v intervalu A´ bude z pohledu ANST v souřadnicích CET o 1 jednotku (sekundu) méně. Zde k-cyklus v CET reprezentuje (k+1) cyklus v ANST a js. Na interval A´ to bude A´/(k+1) proběhlých (k+1)-cyklů, tj. v CET bude ve srovnání s A´ o A´/(k+1) CET jednotek méně.

Počet sekund: A = A´ – A´/(k+1)

V intervalu B´ bude na každý (k-1)-cyklus v ANST, v systému CET naopak o 1 jednotku (sekundu) více než je počet ps. V celém intervalu B´ to bude o B´/(k-1) jednotek více.

Počet sekund: B = B´ + B´/(k-1)

3.4 Základní rovnice pro konstrukci ANST v běžném roce (365 dní)

Parametry rovnic

A₀ – počet CET sekund za půl roku, A₀ = 182,5*24*60*60
A_j´ – počet jarních sekund od začátku roku do bodu obratu, jarní půlrok, A_j´ ≠ A₀
A_p´ – počet podzimních sekund od obratu do konce roku, podzimní půlrok, A_p´ ≠ A₀, A_p´ ≠ A_j´
P´ – časový posun letního bodu obratu v js, maximální posun ANST hodin oproti CET hodinám v js
k – koeficient zrychlení (zpomalení) hodin ANST
Fyzikální jednotky jsou součástí rovnic.

Závorkový formalizmus

( ) – běžný matematický formalizmus

[ ] – například A₀ [s] = (A₀ + P´) [js] znamená A₀ * (1 s) = (A₀ + P´) * (1 js) = (A₀ + P´) * (1 js [s]), výsledkem je číselná rovnice, protože sekundy se vykrátí, 1 js [s] je 1 js v sekundách, 1 js [s] = číslo * (1 s)  

{ } – A₀ {ss} znamená “kvalitativní součet”. Jednotky v závorce sčítáme jako stejné bez ohledu na jejich velikost, pokud mají stejnou kvalitu. Krátké (jarní) a dlouhé (podzimní) sekundy považujeme za jednotky stejné kvality ve smyslu administrativním (účetním) a označujeme je jako sluneční (variabilní) sekundy:

1 {js} =^→ 1 {ss}, 1 {ps} =^→ 1 {ss},         např. 90 {js} + 30 {ps} =^→ 120 {ss}
Pozn.: 1 km = 1000 m, ale 1 {km} ≠ 1000 {m}, výsledná rovnost bilančních rovnic není samozřejmost.

Sluneční (variabilní) sekunda, minuta, hodina nebo den (týden a měsíc) je společný kvalitativní název pro krátkou jarní nebo dlouhou podzimní jednotku času. Víc je v článku o administraci, tj. správě časových systémů a jejich jednotek: https://zimnialetnicas.cz/administrace-prirozeneho-slunecniho-casu/.

Zrychlení a zpomalení hodin

Zrychlení hodin:    k [s] = (k + 1) [js]
Zpomalení hodin: k [s] = (k – 1) [ps]

Pro pochopení rovnic je nejlepší úvodní obrázek kapitoly o ANST, který dává jasný pohled na princip posunu hodinových ručiček. Například pro k = 3 600 platí, že pokud bude v prvním půlroce na CET hodinách „celá“ hodina, na ANST hodinách bude „celá“ +1 js, a pokud bude ve druhém půlroce na CET hodinách „celá“, na ANST hodinách bude za 1 ps „celá“.

Od jednoho k-cyklu k bilanci celého roku

Pokud za půl roku (A₀ sekund) nastane P´ jednotlivých k-cyklů hodin, tak A₀ = P´*k. Vynásobíme jednu i druhou rovnici *P´ a dostaneme:

P´*k [s] = P´*(k + 1) [js]                A₀ [s] = (A₀ + P´) [js]
P´*k [s] = P´*(k – 1) [ps]               A₀ [s] = (A₀ – P´) [ps]

Protože k-cyklus znamená posun ANST hodin o 1 časovou jednotku v [js], číslo P´ reprezentuje celkový posun ANST hodin až do obratu počítaný v [js]. Rovnice pro zrychlení a zpomalení hodin definují zároveň velikost jarní a podzimní jednotky času. Z nich odvozené bilanční rovnice pro každý půlrok jsou s prvními dvěma ekvivalentní. Zpětně se z nich dá odvodit velikost js a ps.

Pro ANST₇₃ platí:    P´ = 182,5*24*60*60/3600 = 4 380 (v js), 4 380 js = 73*60 js = 73 jm
Pro ANST₉₁₁₅ platí: P´ = 182,5*24*60*60/2880 = 5 475 (v js), 5 475 js = 91,25 jm = 91 jm 15 js

Od bilance celého roku k jednomu k-cyklu

Postupovat je možné i opačně, napsat nejdříve bilanční rovnice pro celý rok a z nich odvodit vztahy pro js a ps. Za půl roku dojde k celkovému posunu zrychlených ANST hodin o (+P´) jednotek, zatímco celkový počet sekund bude A₀. Ve 2. půlroce dojde k opačnému posunu o (-P´) jednotek u zpomalených ANST hodin. Počet sekund bude i zde A₀. Jde o zachování celkového počtu časových jednotek v roce.

Rovnice pro js_a:   A_j´ [js] = (A₀ + P´) [js] = A₀ [s]                  (A₀ + P´) [js] = A₀ [s]
Rovnice pro ps_a:  A_p´ [ps] = (A₀ – P´) [ps] = A₀ [s]               (A₀ – P´) [ps] = A₀ [s] 

Pokud P´ = A₀/k

Pro js platí:   1 [js] = (A₀/(A₀ + P´) [s]                      1 [js] = 1/(1+1/k) [s] = (1 – 1/(k + 1)) [s] = k/(k+1) [s]
Pro ps platí: 1 [ps] = (A₀/(A₀ – P´) [s]                      1 [ps] = 1/(1-1/k) [s] = (1 + 1/(k – 1)) [s] = k/(k-1) [s]

V modrém rámečku (vpravo uprostřed) vidíme asymetrii variabilních jednotek vůči délce sekundy.

Zachování celkového počtu jednotek času a celkového časového intervalu pro roční cyklus

Ať už používáme současné jednotky času nebo nové variabilní (sluneční), rok jako administrativní jednotka času musí být „vyrovnaný“. Celková délka časového intervalu musí být pro běžný rok stále stejná, a po příslušné korekci, kdy přičteme k 365 dnům ještě 1 den, musí být délka roku stále stejná také pro přestupný rok. I ten musí mít vždy stejný počet jednotek času (sekund, minut, hodin, týdnů a měsíců), aby administrativní úkony mohly probíhat ve všech časových soustavách ve stejném režimu jako teď.

Pro ověření sečteme rovnice pro jarní a podzimní sekundy a dostaneme:

2A₀ [s] = ((A₀ + P´) [js] + (A₀ – P´) [ps])

Rovnice znamená, že časový interval 1 roku v běžných sekundách a variabilních je stejně dlouhý, protože:

2A₀ = 2*(1/2 roku v sekundách) = 1 rok,
A_j´ [js] = (A₀ + P´) [js], jarní půlrok v [js],
A_p´ [ps] = (A₀ – P´) [ps], podzimní půlrok v [ps],
A_j´ [js] + A_p´ [ps] = 1 rok v [ss].

Počet administrativních jednotek je:

2A₀ [s] = ((A₀ + P´) [js] + (A₀ – P´) [ps])
2A₀ {s} = ((A₀ + P´) {ss} + (A₀ – P´) {ss}) = 2A₀ {ss}

Celkový počet časových jednotek v roce je zachován pro běžné i variabilní jednotky, stejně tak i délka roku jako časového intervalu.

3.5 Vložení jednoho dne do ročního cyklu ANST

Pro systémy typu ANST se využití v přestupném roce (a důsledkem toho ani v jiných letech) zatím nepředpokládá, zejména z důvodu komplikovanějších a méně názorných vlastností časového systému. Přesto zde provedeme prodloužení roku o 1 den i pro systémy typu ANST.

Pro přestupný rok potřebujeme nalézt řešení, kde součet (x₁*js + x₂*ps) dá přesně 24 hod dle CET.

Jedná se o řešení rovnice:

x₁ [js_a] + x₂ [ps_a] = 24*60*60 [s], kde
(x₁ + x₂) = 24*60*60 z důvodu zachování počtu administrativních jednotek času v přestupném roce.

Rovnice pro vložení 24hodinového časového intervalu do ANST₇₃ a ANST₉₁₁₅

(1) Rovnice: x₁ [js_a] + x₂ [ps_a] (= x₁ [js_a] + (24*3600 – x₁) [ps_a]) = 24*60*60 [s]
pro js_a = 3600/3601 s, ps_a = 3600/3599 s
        vede k řešení: x₁ = 43 212 a x₂ = 43 188.

(2) Rovnice: x₁ [js_a] + x₂ [ps_a] (= x₁ [js_a] + (24*3600 – x₁) [ps_a]) = 24*60*60 [s]
pro js_a = 2880/2881 s, ps_a = 2880/2879 s
        vede k řešení: x₁ = 43 215 a x₂ = 43 185.

Pro x₁ platí: x₁ = 12*3600*(k+1)/k = 12*3600/(1 js [s]) 
                     x₂ = 12*3600*(k-1)/k = 12*3600/(1 ps [s]), pokud 1 js = k/(k+1) s, 1 ps = k/(k-1) s

Minimální a dvojitý celočíselný součet, tj. minimální kompaktní CET – ANST interval

Hledáme takový nejmenší časový interval (x₁ + x₂) [s], který je možné složit z x₁ [js_a] + x₂ [ps_a]. Jednotlivé koeficienty a součty musí být celá čísla.

Použijeme předchozí rovnici: x₁ [js_a] + x₂ [ps_a] = (x₁ + x₂) [s],
kde platí 1 js_a = k/(k + 1), 1 ps_a = k/(k – 1) a x₁ + x₂ = x_min. Po úpravách dostaneme:

x₁ = x_min * (k + 1)/2k
x₂ = x_min * (k – 1)/2k Pokud mají být řešením celá čísla x₁ a x₂, tak:
x_min = x₁ + x₂ = 2k,   x₁ = (k + 1),   x₂ = (k – 1)

x₁ * js = ½ * x_min [s] = k [s]
x₂ * ps = ½ * x_min [s] = k [s]

(k + 1) [js_a] + (k – 1) [ps_a] = (k + k) [s], asymetrie [ss] a symetrie [s] kolem bodu obratu 

Pro ANST₇₃ to znamená, že x_min = 7 200 s = 120 min, x₁ = 3 601 (počet js), x₂ = 3 599 (počet ps), dvojice ANST a CET souřadnic jsou (3 601 js + 3 599 ps) = (3 600 s + 3 600 s).

Pro ANST₉₁₁₅ to znamená, že x_min = 5 760 s = 96 min, x₁ = 2 881 (počet js), x₂ = 2 879 (počet ps), dvojice ANST a CET souřadnic jsou (2 881 js + 2 879 ps) = (2 880 s + 2 880 s).

Minimální interval (zde roven dvojitému celočíselnému součtu) pro ANST₇₃ je 120 min a pro ANST₉₁₁₅ 96 min. 24 hod obsahuje 12, resp. 15 násobek těchto intervalů umožňujících celočíselný součet.

Pokud bychom aplikovali stejný postup i na později probírané SNST, dostaneme x_min = 2. To odpovídá skutečnosti, že:
1 js +1 ps = 2 s, na minimální celočíselný součet (ne dvojitý) stačí dvě SNST jednotky.

3.6 Základní rovnice pro konstrukci ANST v přestupném roce (366 dní)

Parametry rovnic

A₀ – počet CET sekund za půl roku, A₀ = 183*24*60*60
A_j´ – počet jarních sekund od začátku roku do bodu obratu, jarní půlrok, A_j´ ≠ A₀
A_p´ – počet podzimních sekund od obratu do konce roku, podzimní půlrok, A_p´ ≠ A₀, A_p´ ≠ A_j´
P´ – časový posun letního bodu obratu v js, maximální posun ANST hodin oproti CET hodinám v js
k – koeficient zrychlení (zpomalení) hodin ANST
Fyzikální jednotky jsou součástí rovnic.

Roční cyklus se prodlouží vložením 24 hod [CET] = 12 hod + 12 hod. Platí rovnice:

Rovnice pro js: A₀ [s] = (A₀ + P´) [js]    ⇔    1 [js] = 1/(1+1/k) [s] = (1 – 1/(k + 1)) [s] = k/(k+1) [s]
Rovnice pro ps: A₀ [s] = (A₀ – P´) [ps]    ⇔   1 [ps] = 1/(1-1/k) [s] = (1 + 1/(k – 1)) [s] = k/(k-1) [s]

Tyto rovnice můžeme používat jako platné i nadále, pouze je v nich jiné A₀ a P´.

Pro ANST₇₃₁₂ platí: P´ = 183*24*60*60/3600 = 4 392 (v js), 4 392 js = (73*60 + 12) js = 73 jm 12 js
Pro ANST₉₁₃₀ platí: P´ = 183*24*60*60/2880 = 5 490 (v js), 5 490 js = 91,5 jm = 91 jm 30 js

Jinou možností je používat už dříve spočtené souřadnice času a k nim dopočítávat jen přírůstky času. V rovnicích pro js a ps provedeme substituci:

 A₀ → A₀ + x, P´ → P´ + y, kde A₀ = 182,5*24*60*60.

Rovnice pro js:  ((A₀ + x) + (P´ + y)) [js] = (A₀ + x) [s]
Rovnice pro ps: ((A₀ + x) – (P´ + y)) [ps] = (A₀ + x) [s]

x je prodloužení půlroku o 12*3 600 sekund (1/2 dne) a
y je další přídavný posun ANST hodin oproti CET hodinám v js

Dodatečný posun y u ANST hodin oproti CET hodinám v js v letním bodě obratu spočteme na základě předchozích dvou rovnic odečtením dřívějších dvou rovnic:

(A₀ + P´) [js] = A₀ [s]
(A₀ – P´) [ps] = A₀ [s].

Pak budou pro časové posuny platit stejné rovnice:
(x + y) [js] = x [s]
(x – y) [ps] = x [s]

Rovnice jsou vzhledem k linearitě vztahů vlastně očekávané a za předpokladu, že:
1 [js]  = k/(k + 1) [s] a
1 [ps] = k/(k – 1) [s], dostaneme v obou případech vztah:

y = x/k, kde x, y, k jsou příslušné parametry rovnic

Přidaná odchylka y pro ANST₇₃₁₂ hodiny od CET intervalu 12 hod je 12*3600/3600 [js] = 12 [js]
Přidaná odchylka y pro ANST₉₁₃₀ hodiny od CET intervalu 12 hod je 12*3600/2880 [js]= 15 [js]

Výsledek plyne z logiky lineárních funkcí. Buď řešíme celý půlroční interval a dostáváme celkový sumární výsledek, nebo hledáme jenom přírůstek, a ten musíme k dřívějšímu výsledku přičíst.

Zachování celkového počtu jednotek času a celkového časového intervalu pro roční cyklus

Sečteme rovnice pro js a ps a získáme počet CET sekund a variabilních sekund v přestupném roce.
((A₀ + x) + (P´ + y)) [js] + ((A₀ + x) – (P´ + y)) [ps] = (2A₀ + 2x) [s]
((A₀ + x) + (P´ + y)) {js} + ((A₀ + x) – (P´ + y)) {ps} = (2A₀ + 2x) {s}, {} – počty kvalitativně stejných jednotek
2(A₀ + x) {ss} = 2(A₀ + x) {s}

Podobně jako v předchozím případě platí i zde, že součtem obou půlroků, jarního v js a podzimního v ps, dostaneme celý rok, a z rovnice
((A₀ + x) + (P + y))*js + ((A₀ + x) – (P + y))*ps = (2A₀ + 2x)*s
plyne, že interval ve [ss] je stejný jako interval v [s]. Pro přestupný rok souhlasí roční časový interval i počet jednotek. Časový systém je konstruován dobře.

3.7 Některé vybrané vlastnosti asymetrického času ANST₇₃

Při pohledu do žluté tabulky vidíme na některých místech zajímavou shodu desetinných čísel a na jiných místech tabulky zas to, že desetinná čísla jsou tam, kde by člověk mohl čekat celá čísla. Je to chyba výpočtu nebo nepřesnost?

Jarní sekunda a jarní hodina

Jarní sekunda je o ∆t = 0,000 277 700 638 711 469 s kratší než sekunda (∆t = 1 s – 1 js)

Délka jarní hodiny je 3 599, 000 277 700 638 711 469 s. Proč to není přesně 3 599 s, a proč je tam stejné desetinné číslo? Je to náhoda nebo chyba?

Platí: 3 601 js = 3 600 s, vyplývá to z definice ANST₇₃
1 jh = 3 600 js = 3 600 s – 1 js = 3 600 s – (1 s – ∆t) = 3 599 s + ∆t

Stejná hodnota časového rozdílu se neobjevuje náhodně ani výpočetní chybou. Od hodiny se odečítá 1 js, ne 1 s, celé číslo je to v js, ale ne v sekundách.

Jarní hodina je od běžné kratší o 1 js, ne o 1 s.

Podzimní sekunda a podzimní hodina

Podzimní sekunda je o ∆t´ = 0,000 277 854 959 711 031 s delší než sekunda (∆t´ = 1 ps – 1 s)

Délka podzimní hodiny je 3601, 000 277 854 959 711 031 s. Opět shoda čísel.

Platí: 3 599 ps = 3 600 s, vyplývá to z definice ANST₇₃
1 ph = 3600 ps = 3600 s + 1 ps = 3600 s + (1 s + ∆t´) = 3601 s + ∆t´

Stejná hodnota časového rozdílu se ani zde neobjevuje náhodně nebo výpočetní chybou. Vidíme, že se přičítá 1 ps, ne 1 s, celé číslo je to v ps, ale ne v sekundách.

Podzimní hodina je od běžné delší o 1 ps, ne o 1 s.

Jarní den v sekundách

Proč má jarní den 86 376,006 664 815 329 075 257 s, proč to není přesně 86 376 s?

Platí: 3 601 js = 3 600 s, vyplývá to z definice ANST₇₃, vynásobíme*24 obě strany rovnice
86 424 js = 86 400 s přesně, na 86 400 js (= 1 jd) musíme odečíst 24 js, ne 24 s.

Jarní den je od běžného kratší o 24 js, ne o 24 s.

Podzimní den v sekundách

Proč má podzimní den 86 424,006 668 519 033 064 740 s, proč to není přesně 86 424 s?

Platí: 3 599 ps = 3 600 s, je to z definice ANST₇₃, vynásobíme*24 obě strany rovnice
86 376 ps = 86 400 s přesně, na 86 400 ps (= 1 jd) musíme připočíst 24 ps, ne 24 s.

Podzimní den je od běžného delší o 24 ps, ne o 24 s.

Složitější asymetrické vztahy mohou na první pohled vypadat jako výpočetní chyba. A nejen zde.

3.8 Paradox ANST hodin

P´*k [s] = P´*(k + 1) [js]               ⇔         A₀ [s] = (A₀ + P´) [js]
P´*k [s] = P´*(k – 1) [ps]               ⇔         A₀ [s] = (A₀ – P´) [ps]

P´ je v obou rovnicích stejné číslo z důvodu zachování počtu “administrativních” jednotek času v roce. Z hlediska prvního půlroku můžeme říci, že se hodiny posunou o P´ js dopředu, ale z hlediska druhého půlroku se hodiny posunou o P´ ps dozadu.

Platí: 1 js ≠ 1 ps, a proto P´*(1 js) ≠ P´*(1 ps). Jak je potom možné, že se hodiny v jednom půlroce posunou o P´ jednotek dopředu, ve druhém o P´ jednotek dozadu, a nakonec se po této „operaci“ vrátí zpět do neposunutého stavu shodného s CET časem, když je velikost jednotek času ANST (js a ps) odlišná? Jednotky nejsou stejné ani v symetrii prodloužení nebo zkrácení. Prodloužení dlouhé sekundy není stejné jako zkrácení krátké sekundy.

Tato otázka, stejně jako mnoho dalších, patří k záludnostem asymetricky konstruovaných časů. Zde rovnost nastane až po součtu (A₀ + P´) nebo (A₀ – P´) a následném součinu s [js] nebo [ps]. Až potom platí, že
((A₀ + P´) js [s] = ((A₀ – P´) ps [s] = A₀ [s]. Rovnice nejsou problémem, ale běžné úvahy o čase ano.

Logická (symetrická) úvaha totiž říká, že pokud časový (nebo prostorový interval) rozdělíme na dvě stejné půlky A₀, tak když k první ½ intervalu něco přidáme, tak od druhé ½ intervalu musíme to samé odečíst, aby součet nových délek dal tu původní (A₀ + d) + (A₀ – d) = 2A₀. V symetrickém světě platí, že když se něco od něčeho odečte, musí se to samé i přičíst, aby vznikl původní celek.

Tady se odečítání a sčítání neodehrává od stejné hodnoty A₀, ale od různých hodnot A₀*js nebo A₀*ps. Zdánlivě k hodnotě A₀ přičítáme P´, ve skutečnosti k zkrácené hodnotě A₀*js přičítáme opět zkrácené P´*js. Až jejich součtem dostaneme A₀, ne (A₀ + P´). Už to svědčí o předchozí deformaci.

Ve druhém případě pro ps také neodečítáme P´ od A₀. Ve skutečnosti od prodloužené hodnoty A₀*ps odečítáme prodloužené P´*ps. Výsledkem je opět A₀, ne (A₀ – P´). Proto vzniká zdánlivá absurdita, že například u ANST₇₃ se první půlrok hodinky posunou o 73 jm dopředu, druhý o 73 pm dozadu, a přesto, že se jedná o různě velké jednotky, celkový interval času jednoho roku se zachová.

V běžném životě ale neuvažujeme v rovnicích, používáme jednoduché úvahy, a to může být problém. Otázkou je, jaké další zdánlivé paradoxy a „klamy“ může takto měřený čas přinést. Zda se nemůže stát, že v nějaké klíčové situaci dojde při analýze nějakého problému k dezorientaci a chybné úvaze.

CET hodiny si za 1. půlrok odtikají A₀ sekund a ANST hodiny ve stejné době odtikají (A₀ + P´) js. Ve 2. půlroce CET hodiny odtikají opět A₀ sekund, ale ANST hodiny jen (A₀ – P´) ps. ANST hodiny tikají 1. půlrok o P´ časových jednotek víc než CET a 2. půlrok o P´ časových jednotek míň než CET.

Další rozvoj asymetrických časových systémů

Z těchto důvodů byly pro další výpočty a optimalizaci časových systémů vybrané a rozvíjené už jen symetrické systémy, pro jednodušší vlastnosti i krásu symetrie. Běžné úvahy o čase jsou v symetrických systémech daleko názornější a jednodušší než stejné úvahy v asymetrických systémech.

4. Symetrický přirozený sluneční čas (SNST)

Jak bylo v předchozích kapitolách vidět, u asymetrického času počet jarních a podzimních časových jednotek v roce není stejný. Proto ani jejich prodloužení nebo zkrácení vůči běžné sekundě není stejné. Vztahy a představy o průběhu času vyžadují nepřirozené asymetrické uvažování. Symetrický přístup je nám bližší a při řešení malých časových úkolů v běžném životě je daleko názornější.

Proto je užitečné a příjemné nastavit rovnice na stejný počet jarních a podzimních sekund, aby byla délka jarních a podzimních sekund vůči běžné sekundě symetrická. Obrat v běžném roce potom nastane vždy 183. den ve 12:00:00 NST (183. den v 10:47:00 dle CET pro SNST₇₃). Takto definovaný čas je vhodnější pro praktické použití a umožňuje elegantní řešení problematiky přestupného roku.

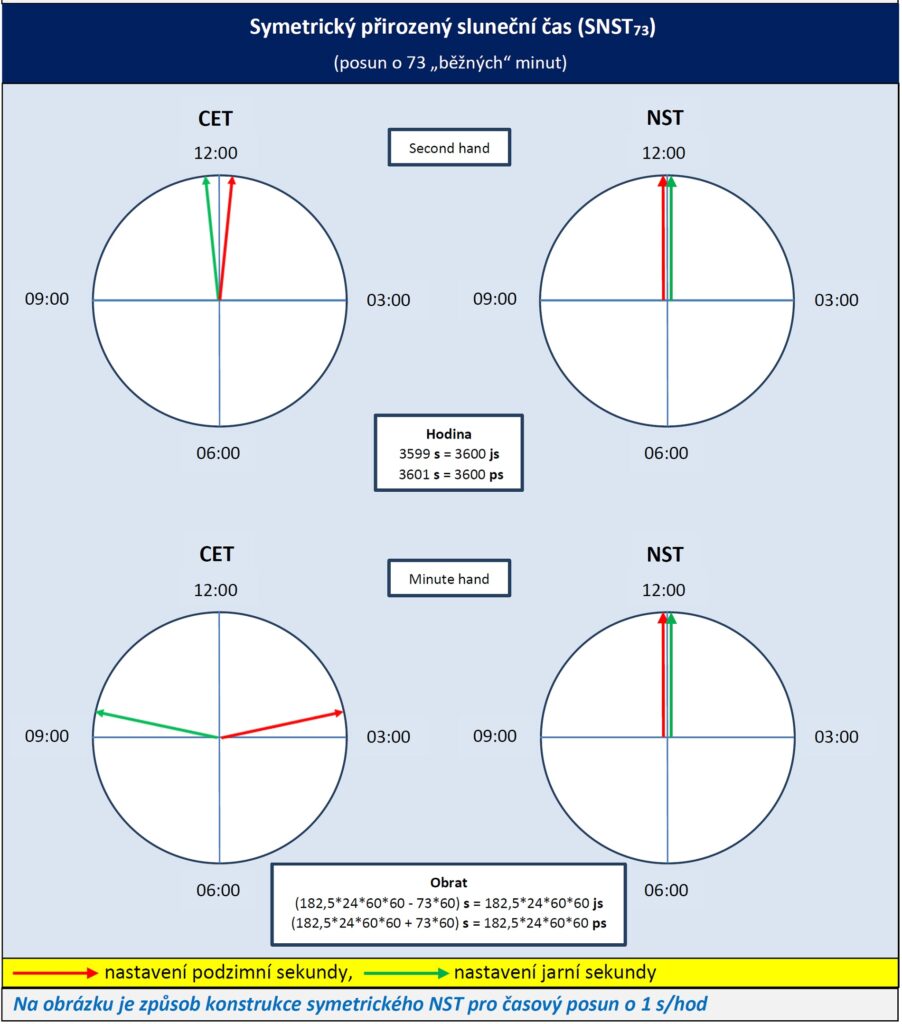
Jako první verze symetrického časového systému se nabízí varianta s posunem o 1 s/hod. V tomto případě ale nebude zrychlený (zpomalený) systém NST porovnán s celou hodinou SEČ, ale naopak „celá“ hodina NST bude porovnána s pomalejším (rychlejším) SEČ. Tato zdánlivě bezvýznamná a malicherná změna znamená výraznou změnu rovnic a následných vlastností časového systému.

4.1 Symetrický přirozený sluneční čas SNST₇₃

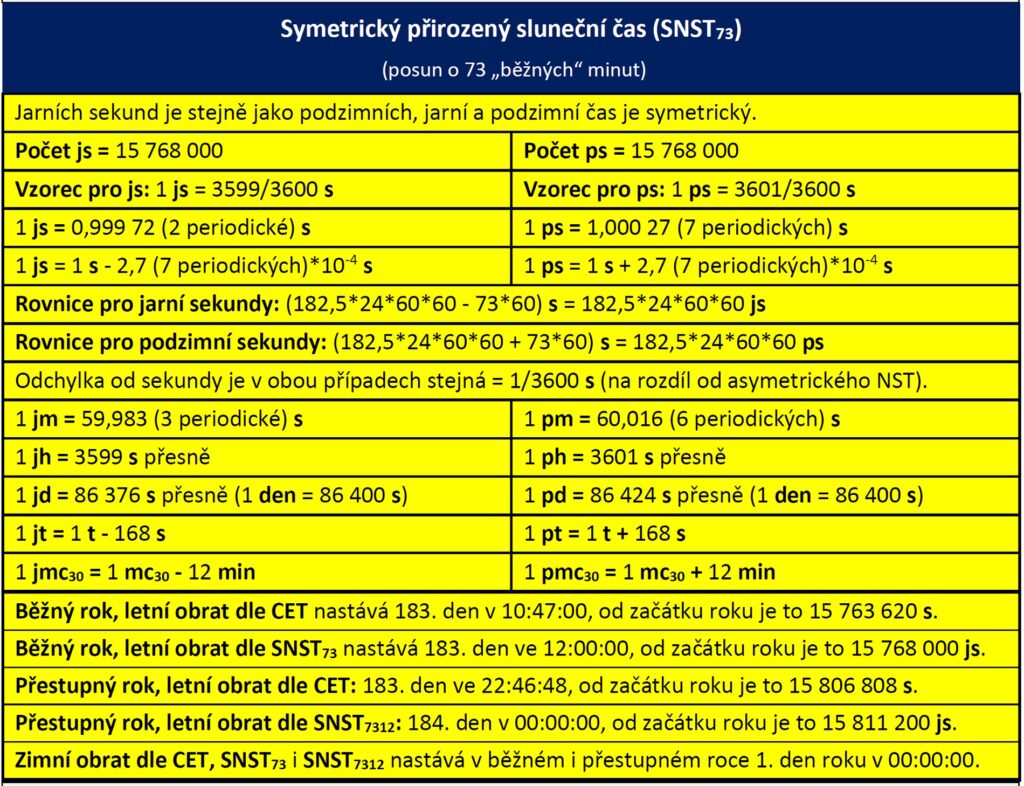
Parametry rovnic

A – počet sekund od začátku roku do daného okamžiku, ale maximálně do bodu obratu [s]
B – počet sekund od bodu obratu do daného okamžiku, ale maximálně do konce roku [s]
C = A + B – celkový počet sekund od začátku roku do daného okamžiku [s]

A´ – počet js od začátku roku do daného okamžiku, ale maximálně do bodu obratu [js]
B´ – počet ps od bodu obratu do daného okamžiku, ale maximálně do konce roku [ps]
C´ = A´ + B´ – celkový počet slunečních sekund od začátku roku do daného okamžiku [ss]

Přepočet CET → SNST₇₃
SNST₇₃ [ss] = A´ + B´ = A/(js [s]) + B/(ps [s]) = A * 3600/3599 + B * 3600/3601 = C + (A/3599 – B/3601)

Přepočet SNST₇₃ → CET
CET [s] = A + B = A´/(s [js]) + B´/(s [ps]) = A´ * 3599/3600 + B´ * 3601/3600 = C´ + (B´ – A´)/3600

Jako druhá verze symetrického časového systému se nabízí varianta s posunem o 1,25 s/hod. Systém konstrukce rovnic zůstává zachován. Zvětšení časového rozdílu znamená, že celkový posun do letního bodu obratu bude větší, až 91 min a 15 s. To v praxi znamená, že bude využita větší část 4hodinového časového rozdílu mezi východy Slunce v zimě a v létě na 50. rovnoběžce.

4.2 Symetrický přirozený sluneční čas SNST₉₁₁₅

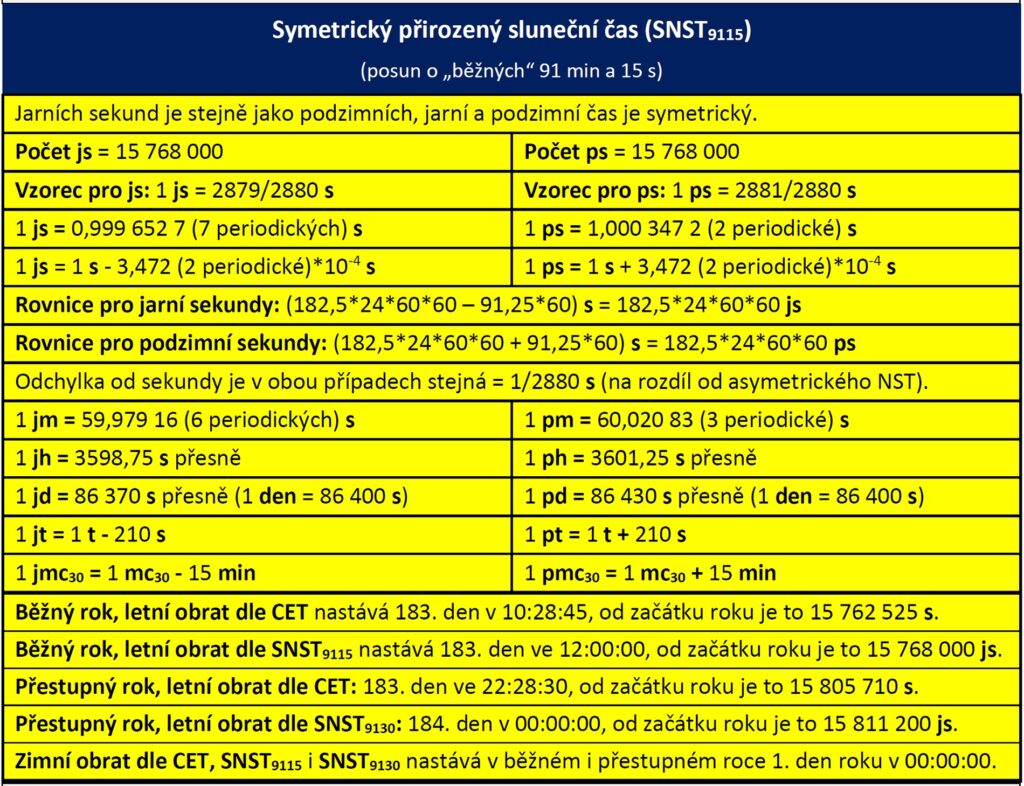
Parametry rovnic

A – počet sekund od začátku roku do daného okamžiku, ale maximálně do bodu obratu [s]
B – počet sekund od bodu obratu do daného okamžiku, ale maximálně do konce roku [s]
C = A + B – celkový počet sekund od začátku roku do daného okamžiku [s]

Parametry rovnic

A₀ – počet CET sekund za půl roku, A₀ = 182,5*24*60*60
A_j´ – počet jarních sekund od začátku roku do bodu obratu, jarní půlrok, A_j´ = A₀
A_p´ – počet podzimních sekund od obratu do konce roku, podzimní půlrok, A_p´ = A₀
P – časový posun letního bodu obratu v [s], maximální posun CET hodin oproti SNST hodinám v [s]
k – koeficient zrychlení (zpomalení) hodin SNST
Fyzikální jednotky jsou součástí rovnic.

Zrychlení a zpomalení hodin

Zrychlení hodin: k [js] = (k – 1) [s]
Zpomalení hodin: k [ps] = (k + 1) [s]

Pro pochopení rovnic je nejlepší úvodní obrázek, který dává jasný pohled na princip posunu hodinových ručiček. Například pro k = 3600 platí, že každá celá hodina v prvním půlroce nastane na SNST₇₃ hodinách, když bude na CET hodinách za 1 s „celá“, a každá celá hodina ve druhém půlroce nastane na SNST₇₃ hodinách, když bude na CET hodinách „celá“ + 1 s.

Od jednoho k-cyklu k bilanci celého roku

Pokud za půl roku (A₀ sekund) nastane počet P jednotlivých (k-cyklů) hodin, tak A₀ = P*k. Vynásobíme jednu i druhou rovnici *P a dostaneme:

P*k [js] = P*(k – 1) [s]                   A₀ [js] = (A₀ – P) [s]
P*k [ps] = P*(k + 1) [s]                 A₀ [ps] = (A₀ + P) [s]

Protože k-cyklus znamená posun o jednu CET časovou jednotku v [s], P reprezentuje celkový posun CET hodin až do obratu počítaný v [s]. Rovnice pro zrychlení a zpomalení hodin definují zároveň velikost jarní a podzimní jednotky času. Z nich odvozené “bilanční” rovnice pro každý půlrok jsou s prvními dvěma ekvivalentní. Zpětně se z nich dá odvodit velikost js a ps.

Pro SNST₇₃ platí: P = 182,5*24*60*60/3600 = 4380 (v [s]), 4380 s = 73*60 s = 73 min
Pro SNST₉₁₁₅ platí: P = 182,5*24*60*60/2880 = 5 475 (v [s]), 5 475 s = 91,25 min = 91 min 15 s

Od bilance celého roku k jednomu k-cyklu

Postupovat je možné i opačně a napsat nejdříve bilanční rovnice pro celý rok. Z nich potom dostáváme vztahy pro js a ps. Za půl roku dojde k celkovému posunu CET hodin o (-P) jednotek, zatímco počet js bude A₀. Ve druhém půlroce musí dojít k opačnému posunu o (+P) jednotek u CET hodin. Počet ps bude i zde A₀. Jde o zachování celkového počtu časových jednotek v roce.

Rovnice pro js_s: (A₀ – P) [s] = A_j´ [js] = A₀ [js]                       (A₀ – P) [s] = A₀ [js]
Rovnice pro ps_s: (A₀ + P) [s] = A_p´ [ps] = A₀ [ps]                  (A₀ + P) [s] = A₀ [ps]

Pokud P = A₀/k

Pro js platí: 1 [js] = (1 – P/A₀) [s]               1 [js] = (1 – 1/k) [s] = (k – 1)/k [s]
Pro ps platí: 1 [ps] = (1 + P/A₀) [s]            1 [ps] = (1 + 1/k) [s] = (k + 1)/k [s]

V modrém rámečku (vpravo uprostřed) vidíme symetrii variabilních jednotek vůči délce sekundy.

Zachování počtu administrativních jednotek času a časového intervalu pro roční cyklus

Pro ověření sečteme rovnice pro jarní a podzimní sekundy a dostaneme: 2A₀ [s] = (A₀ [js] + A₀ [ps]). Délka roku jako časového intervalu je zachována pro běžné i variabilní jednotky. Pro počet jednotek v roce platí: 2A₀ {s} = 2A₀ {ss}. Celkový počet jednotek v roce je zachován.

4.5 Vložení jednoho dne do ročního cyklu SNST

Vložení jednoho dne do ročního cyklu SNST na základě úvah

Jak řešit přestupný rok, tj. jeden vložený den o 24 hodinách složených z běžných sekund a minut v rámci nově navrženého systému s přirozeným slunečním časem? Odpověď je velmi jednoduchá. Využijeme SNST a posuneme letní obrat o 12 jh. Obrat nenastane 183. den ve 12:00:00, ale 184. den v 00:00:00 dle SNST. Oproti normálnímu roku necháme běžet jarní čas ještě dalších 12 jarních hodin.

Protože na celý vložený den potřebujeme 24 hod, a navíc se dodatečný časový rozdíl mezi variabilním časem a CET časem musí vrátit do bodu na začátku této „operace“, aby nebyl narušen „chod a jízdní řád“ dříve navrženého časového systému pro 365 dní, necháme 12 ph běžet i podzimní čas. Dodatečný časový rozdíl se tak vrátí zpět a v intervalu 24 hod bude nulový. Tím vložíme 24 hod dle CET zároveň jako 24 slunečních hodin dle SNST a zachováme symetrii SNST.

Platí: 12 jh + 12 ph = 12*3600 js + 12*3600 ps = 12*3600*((1 – Δt) + (1 + Δt)) s = 24 hod
Δt – posun js, resp. ps oproti běžné sekundě (pro SNST obecně je interval pro obě sekundy stejný)

24 slunečních hodin je v tomto případě svojí délkou přesně rovno 24 hodinám dle CET.

Vložení jednoho dne do ročního cyklu SNST na základě rovnic

Předchozí úvahy ilustrují jednoduchost a názornost práce s časovými systémy typu SNST. Řešení bylo možné zkonstruovat i bez rovnic na základě jednoduchých úvah. Je ale možné postupovat i podle rovnic jako u systémů typu ANST.

Pro přestupný rok potřebujeme nalézt řešení, kde součet (x₁*js + x₂*ps) dá přesně 24 hod dle CET.

Jedná se o řešení rovnice:
x₁ [js_s] + x₂ [ps_s] = 24*60*60 [s], kde
(x₁ + x₂) = 24*60*60 z důvodu zachování počtu administrativních jednotek času v přestupném roce.

Rovnice pro vložení 24hodinového časového intervalu do SNST₇₃ a SNST₉₁₁₅

(1) Rovnice: x₁ [js_s] + x₂ [ps_s] (= x₁ [js_s] + (24*3600 – x₁) [ps_s]) = 24*60*60 [s]
pro js_s = 3599/3600 s, ps_s = 3601/3600 s
        vede k řešení: x₁ = 43 200 a x₂ = 43 200.

(2) Rovnice: x₁ [js_s] + x₂ [ps_s] (= x₁ [js_s] + (24*3600 – x₁) [ps_s]) = 24*60*60 [s]
pro js_s = 2879/2880 s, ps_s = 2881/2880 s
        vede k řešení: x₁ = 43 200 a x₂ = 43 200.

Pro x₁ platí: x₁ = 12*3600
                      x₂ = 12*3600, pokud 1 js = (k-1)/k [s], 1 ps = (k+1)/k [s], řešení je pro oba systémy stejné.

Minimální a dvojitý celočíselný součet, tj. minimální kompaktní CET – SNST interval

Hledáme takový nejmenší časový interval (x₁ + x₂) [s], který je možné složit z x₁ [js_s] + x₂ [ps_s]. Jednotlivé koeficienty a součty musí být celá čísla.

Použijeme předchozí rovnici: x₁ [js_s] + x₂ [ps_s] = (x₁ + x₂) [s],
kde platí 1 js = (k-1)/k [s], 1 ps = (k+1)/k [s] a x₁ + x₂ = x_min. Po úpravách dostaneme:

x₁ = x_min/2
x₂ = x_min/2   Pokud mají být řešením celá čísla x₁ a x₂, tak: x_min = 2,   x₁ = 1,   x₂ = 1

1 [js] + 1 [ps] = ((k-1)/k + (k+1)/k) [s] = 2 [s] 

Minimální základní interval pro SNST₇₃ i pro SNST₉₁₁₅ jsou 2 s. Denní cyklus času (24 hod) potom obsahuje 43 200 násobek těchto minimálních intervalů umožňujících celočíselný součet.

Dvojitý celočíselný součet nastane pro:

k [js_s] + k [ps_s] = (k-1) [s] + (k+1) [s], symetrie [ps_s] a asymetrie [s] kolem bodu obratu

Je to analogická situace jako u ANST. Pro SNST₇₃ to znamená interval 7 200 s = 120 min, dvojice SNST a CET souřadnic jsou (3 600 js + 3 600 ps) = (3 599 s + 3 601 s). Pro SNST₉₁₁₅ to znamená 5 760 s = 96 min, dvojice SNST a CET souřadnic jsou (2 880 js + 2 880 ps) = (2 879 s + 2 881 s).

4.6 Základní rovnice pro konstrukci SNST v přestupném roce (366 dní)

Parametry rovnic

A₀ – počet CET sekund za půl roku, A₀ = 183*24*60*60
A_j´ – počet jarních sekund od začátku roku do bodu obratu, jarní půlrok, A_j´ = A₀
A_p´ – počet podzimních sekund od obratu do konce roku, podzimní půlrok, A_p´ = A₀
P – časový posun letního bodu obratu (maximální posun CET hodin oproti SNST hodinám v [s])
k – koeficient zrychlení (zpomalení) hodin SNST
Fyzikální jednotky jsou součástí rovnic.

Roční cyklus se prodlouží vložením 24 hod [CET] = 12 jh + 12 ph. Platí rovnice:

Rovnice pro js: (A₀ – P) [s] = A₀ [js]          ⇔       1 [js] = (1 – 1/k) [s] = (k – 1)/k [s]
Rovnice pro ps: (A₀ + P) [s] = A₀ [ps]       ⇔       1 [ps] = (1 + 1/k) [s] = (k + 1)/k [s]

Tyto rovnice můžeme používat jako platné i nadále, pouze je v nich jiné A₀ a P.

Pro SNST₇₃₁₂ platí: P = 183*24*60*60/3600 = 4 392 (v [s]), 4 392 s = (73*60 + 12) s = 73 min 12 s
Pro SNST₉₁₃₀ platí: P = 183*24*60*60/2880 = 5 490 (v [s]), 5 490 s = 91,5 min = 91 min 30 s

Jinou možností je používat dříve spočtené souřadnice času a k nim dopočítávat jen přírůstky. V rovnicích pro js a ps provedeme substituci

A₀ → A₀ + x, P → P + y, kde A₀ = 182,5*24*60*60.

Rovnice pro js: ((A₀ + x) – (P + y)) [s] = (A₀ + x) [js]
Rovnice pro ps: ((A₀ + x) + (P + y)) [s] = (A₀ + x) [ps]

Dodatečný posun y u CET hodin oproti SNST hodinám v sekundách v letním bodě obratu spočteme na základě předchozích dvou rovnic odečtením:
(1) (A₀ – P) [s] = A₀ [js] a
(2) (A₀ + P) [s] = A₀ [ps]

Pak bude platit:

(x – y) [s] = x [js]
(x + y) [s] = x [ps]

Rovnice jsou vzhledem k linearitě vztahů vlastně očekávané a za předpokladu, že:
1 [js]  = (k – 1)/k [s] a
1 [ps] = (k + 1)/k [s], dostaneme v obou případech očekávaný vztah:

y = x/k, kde x, y, k jsou příslušné parametry rovnic 

x je prodloužení o (1/2 dne) = 12*3 600 [s] a
y je další přídavný posun CET hodin oproti SNST hodinám v [s]

Přidaná odchylka (zpoždění) y CET hodin oproti SNST₇₃₁₂ je za 12 jh: 12*3600/3600 = 12 [s]
Přidaná odchylka (zpoždění) y CET hodin oproti SNST₉₁₃₀ je za 12 jh: 12*3600/2880 = 15 [s]

Výsledek plyne z logiky lineárních funkcí. Buď řešíme celý půlroční interval a dostáváme celkový sumární výsledek, nebo hledáme jenom přírůstek, a ten musíme k dřívějšímu výsledku přičíst.

Přirozený sluneční čas se v přestupném roce během prvních 12 jh posune vůči CET v případě SNST₇₃₁₂ o dalších 12 běžných sekund a v průběhu následujících 12 ph se o stejných 12 běžných sekund vrátí zpět (pro SNST₉₁₁₅ by to bylo o 15 sekund tam a zase zpět). Zbytek roku před a po této „operaci“ je stejný jako v běžném roce s 365 dny. Křivky SNST₇₃ a SNST₉₁₁₅ prodloužené na přestupný rok jsou značené jako SNST₇₃₁₂ a SNST₉₁₃₀.

Zachování počtu administrativních jednotek času a časového intervalu pro roční cyklus

Sečteme rovnice pro js a ps a dostaneme časový interval pro přestupný rok: 2(A₀ + x) [s] = (A₀ + x) [js] + (A₀ + x) [ps]. Délka roku jako časového intervalu je zachována pro běžné i variabilní jednotky. Pro počet jednotek v roce platí: 2(A₀ + x) {s} = 2(A₀ +x) {ss}. Počet jednotek je zachován. Časový systém je konstruován dobře.

Obrat SNST₇₃₁₂ spočtený jako přírůstek a posun času k běžnému roku

Letní obrat dle CET: x [js] = (x – y) [s]. 12 jh = 12 hod – 12 s, v CET se obrat posune o tuto hodnotu z původních 10:47:00. Obrat nastane 183. den ve 22:46:48. Od začátku roku uběhne 15 806 808 s. Čas na CET hodinách se bude zpožďovat o dalších 12 s.

Letní obrat dle SNST₇₃₁₂: x [js] = (x – y) [s]. Vložení dalších 12 jh do ročního cyklu znamená posun obratu o 12 jh = 12*3 600 js = 43 200 js. Původní obrat je v běžném roce ve 12:00:00, posunutý nastane 184. den v 00:00:00, od začátku roku uběhne 15 811 200 js.

Obrat SNST₉₁₃₀ spočtený jako přírůstek a posun času k běžnému roku

Letní obrat dle CET: x [js] = (x – y) [s]. 12 jh = 12 hod – 15 s, v CET se obrat posune o tuto hodnotu z původních 10:28:45. Obrat nastane 183. den ve 22:28:30. Od začátku roku uběhne 15 805 710 s. Čas na CET hodinách se bude zpožďovat o dalších 15 s.

Letní obrat dle SNST₉₁₃₀: x [js] = (x – y) [s]. Vložení dalších 12 jh do ročního cyklu znamená posun obratu o 12 jh = 12*3 600 js = 43 200 js oproti obratu v běžném roce ve 12:00:00. Nový obrat nastane 184. den v 00:00:00, od začátku roku uběhne 15 811 200 js.

4.7 Sčítání a odečítání u SNST hodin graficky

Schémata ukazují podstatný rozdíl mezi ANST a SNST. Hodinky v bodě letního obratu ukazují u ANST (A₀ + P´) časových jednotek, o P´ víc než CET hodiny. U SNST je to stejné číslo zde značené jako P, ale v sekundách. Rozdíl je v tom, že u ANST vzniká paradox, že se hodiny posunou o P´ js tam, pak o P´ ps zpět, a přesto se nakonec dostanou do výchozího bodu. U SNST hodin se hodiny posunou o P sekund nejdříve tam, a pak o stejných P sekund zpět. Bez paradoxů, jasně a pochopitelně.

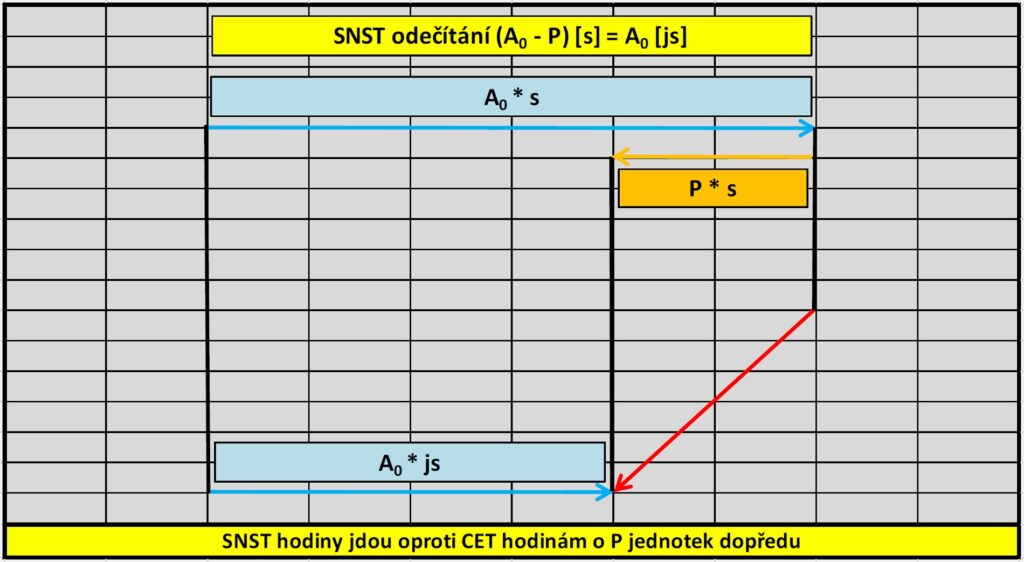
SNST hodiny v 1. půlroce odtikají A₀ js a ve 2. půlroce A₀ ps. CET hodiny si za 1. „jarní“ půlrok odtikají (A₀ – P) sekund a za 2. „podzimní“ půlrok (A₀ + P) sekund.

4.8 Konstantní posuny časového systému SNST značené jako (-)

Optimalizace časového systému konstantním posunem stupnice

Na základě dříve uvedených rovnic je možné konstruovat časové systémy typu SNST s využitím základních rovnic, a tyto můžeme následně dál optimalizovat tak, že seřídíme časovou stupnici SNST i numericky. Čísla, reprezentující časové souřadnice, musí co nejlépe odpovídat současnému rozvrhu hodin spojenému s východy a západy Slunce jako nejdůležitějšími body NST.

V tabulkách (viz odkazy na začátku článku) se nachází systémy SNST₇₃₁₂ a SNST₉₁₃₀, vytvořené pro přestupný rok 2020 a SNST₇₃₁₂ (-) a SNST₉₁₃₀ (-), konstruované z předchozích odečtením konstantního časového intervalu Δt tak, aby v létě Slunce nezapadalo „numericky“ později než dnes. Pro první křivku je Δt = 13 „min“ 12 „s“, pro druhou je Δt = 31 „min“ 30 „s“. Posunuté jsou všechny body křivek, včetně obou obratů. Optimalizace posunem časové škály byla v článku „Správný čas“ provedena i z hlediska dalších parametrů pro hodnocení časových systémů.

Položme si proto otázku, co toto numerické odečítání vlastně znamená? Z hlediska matematiky na odečítání není nic zajímavého. Každý bod funkce (křivky) posuneme o stejnou konstantu:

y₂(x) = y₁(x) ± konstanta

Intervaly mezi body y se v takovém případě nemění. Tak proč to vůbec zkoumat? Protože se tu nejedná o úplně obyčejné křivky, jsou to křivky, které popisují čas a z technického hlediska chod hodin. Vzniká proto oprávněná otázka, co a jak se vlastně posouvá. Pokud „přetáčíme“ současné hodiny, kde jsou časové intervaly stejné, časový posun je taky všude stejný, ale co to znamená u hodin, kde se jednotky času mění? Tam už to není tak samozřejmé.

Jaké jednotky vlastně aplikujeme, když odečítáme v každém řádku tabulky jedno stejné číslo (např. 13 „min“ a 12 „s“). Jsou to současné běžně známé sekundy a minuty, nebo jsou to jarní jednotky, nebo podzimní? Nebo se v řádcích, kde jsou jarní jednotky, odečítají ty, a v řádcích, kde jsou podzimní jednotky se odečítají zas ty druhé? Nemůže se potom celé měření „rozejít“ do naprosto nesmyslných a bezcenných údajů, které nebudou nikdy udávat správný čas?

Formální matematická funkce dává tušit, že výpočet by měl být „asi“ dobře, ale otázek je příliš mnoho a za odpověď rozhodně stojí. Můžeme například zkonstruovat „základní“ hodiny jako SNST₇₃₁₂ nebo SNST₉₁₃₀, a až pak, před digitálním zobrazením na číselníku odečteme X čísel. Základní časový systém SNST považujeme za prozkoumaný a funkční. Posunuté (přetočené) hodinky (-) proto musí také fungovat, protože na samotných číslech nezáleží, pokud jsou zachovány intervaly času.

Odečítání stejného čísla znamená, že intervaly času se nemění, kde byly jarní jednotky, tam budou i nadále, a kde byly podzimní jednotky, tam také zůstanou. Intervaly se v čase nikam neposouvají, mění se jen jim přiřazené hraniční numerické hodnoty. Navzorkované intervaly času zůstávají.

Body obratu z hlediska posunu křivky

Body obratu jsou u SNST₇₃₁₂ nebo SNST₉₁₃₀ fixované na roční období, proto je v CET nemůžeme výrazně měnit už z podstaty věci. Otázkou ale je, zda posun souřadnic SNST neposune nechtěně obrat i v CET. Letní obrat je matematicky změna směrnice křivky, přičtení konstanty neovlivní polohu této změny na ose x. Při konstantním posunu křivky SNST se proto obrat v CET nemění.

Obrat se v CET nikam nepřesouvá. K danému fyzikálnímu času jen potřebujeme namapovat jinou hodnotu ukazatele času SNST. Je to podobné jako teď, když ke stejné hodnotě času přiřadíme letní čas. Proto se obrat na ose y (v jednotkách SNST) posune, ale na ose x, kde je vlastní tok času, ne.

Body obratu v jednotkách SNST získáme odečtením příslušných numerických hodnot:

Platí: SNST₇₃₁₂ (-) = SNST₇₃₁₂ – 13:12 (zimní obrat v SNST už nebude v bodě nula)
          SNST₉₁₃₀ (-) = SNST₉₁₃₀ – 31:30 (ani zde zimní obrat v SNST už nebude v bodě nula)

„Přetočení“ ciferníku o X jednotek znamená, že o stejný počet čísel posuneme v SNST jak zimní, tak letní obrat, a s nimi všechny namapované časové souřadnice.

Kdy nastane silvestrovská půlnoc?

Jaký vliv bude mít odečítání numerických hodnot na půlnoc? Když ručičky na „základních“ (nepřetočených) SNST hodinách přetočíme na Silvestra o půlnoci (dle CET i SNST) o X jednotek zpět (odečítání znamená, že na hodinách bude menší číslo, proto otáčíme proti směru hodinových ručiček), zimní obrat v SNST posuneme numericky a administrativně na předchozí den.

Důležité je, že stupnice SNST se tím vůči CET neposouvá jako celek jedním ani druhým směrem jako při běžné představě posunu časové škály, která má stejné intervaly času. Podzimní jednotky se proto nepřesunou ani jedním, ani druhým směrem a skončí o půlnoci. Stupnice jako vzor pro mapování časových souřadnic zůstává, je jen přečíslovaná z důvodu „seřízení“ s rozvrhem hodin.

SNST po obratu pokračují v js, protože js po půlroce nahrazují ps. Půlnoc tedy budeme na NST hodinách slavit už v js. Po časovém intervalu 13:12 nebo 31:30 (v jm a js přesně), měřeném od tradiční CET půlnoci nastane i na SNST hodinách půlnoc jako čas 00:00:00.

V tomto případě budeme půlnoc na Silvestra slavit 2x.

První půlnoc nastane dle CET hodin, dnes tuto půlnoc považujeme za začátek nového dne i roku. Tady bude spojena hlavně s obratem, změnou dlouhé podzimní sekundy na krátkou jarní a po cca 13 jm nebo 31 jm (dle vybrané verze SNST) nastane po dosažení časové souřadnice 00:00:00 druhá půlnoc, jako začátek nového dne i kalendářního roku dle SNST. Jediným problémem bude nutnost opatřit si dvě láhve šampaňského.

Posuny hodin dopředu a zpět

Posun hodin dopředu (ve směru hodinových ručiček)

Všechny události svázané s hodinkami a rozvrhem hodin nastanou ve srovnání s CET skutečně dříve (poledne ve 12:00:00 i ranní vstávání, začátek práce, odchod autobusu). Děje nesvázané s hodinkami budou dle nových posunutých souřadnic probíhat zdánlivě později (pravé poledne, východy i západy Slunce).    

Posun hodin zpět (proti směru hodinových ručiček)

Všechny události svázané s hodinkami a rozvrhem hodin nastanou ve srovnání s CET skutečně později (silvestrovská půlnoc v 00:00:00 i ranní vstávání, začátek školy, odchod autobusu). Děje nesvázané s hodinkami budou dle nových posunutých souřadnic probíhat zdánlivě dříve (východy i západy Slunce, pravé poledne).

Převzorkování a nová mapa časových souřadnic

Z předchozích úvah je vidět, že z důvodu optimalizace časových systémů typu NST potřebujeme někdy manipulovat s časovými souřadnicemi (posouvat je). Pokud se pro uvažovanou událost časové souřadnice ve strojovém čase (CET) nemění, budou v rovnicích pro převod souřadnic časových systémů platit pro danou událost stále stejné koeficienty A i B v sekundách.

To znamená, že u takové události (např. východ Slunce) se nezmění ani A´, ani B´ (počet js a ps bude stejný) a vzor (hranice a šířka intervalů) pro mapování času systémem SNST zůstává. Časové jednotky se nezmění v CET ani v SNST. Posouváme jen čísla na ciferníku, ale ne časové intervaly (měřítko). Obrat v SNST a všechny ostatní hodnoty času pro danou událost budou pouze přečíslované.

Letní obrat se nachází na konci intervalu s [js]: A_j´ = A_p´ = A₀´ (jarní půlrok = 182,5*24*3 600 js)

Pak bude platit přepočet CET → SNST       SNST [ss] = A₀´ = A₀/(js [s])
                         a přepočet SNST → CET        CET [s] = A₀ = A₀´/(s [js])

Po provedení konstantního posunu (-) v SNST platí:

 A₀´(-) = A₀´ + konst
 A₀´(-) = A₀/(js [s]) + konst
 A₀/(js [s]) = A₀´(-) – konst = A₀´
 A₀ = A₀´*(js [s]) = A₀´/(s [js]), protože js [s] = 1/(s [js])

Souřadnice obratu v CET se nezměnila, jak se dalo očekávat. Interval js začíná na začátku kalendářního roku a končí letním obratem. Interval ps začíná letním obratem a končí na konci roku. Vzor krátkých a dlouhých sekund zůstává vzhledem k CET „na místě“, tzn. že se v CET souřadnicích nemění.

Vzor pro číselné mapování znamená, že v intervalu 0 až A₀´ jsou namapované intervaly pro js a od A₀´ do B₀´ jsou namapované intervaly pro ps. K nim se potom přiřadí časové souřadnice 0 – 24 sh.

Pokud ale posuneme zimní nebo letní obrat i v CET (pro zachování symetrie musíme posunout oba), časové měřítko SNST se posune a převzorkuje daný interval času, a ten bude „namapován“ jinak. Rovnice se změní a odečítat konstantu už nebude stačit. Pro danou událost, například východy a západy Slunce bude potřebný nový výpočet.

5. Vlastnosti a charakteristiky časových systémů

5.1 Odchylky mezi symetrickými a asymetrickými sekundami

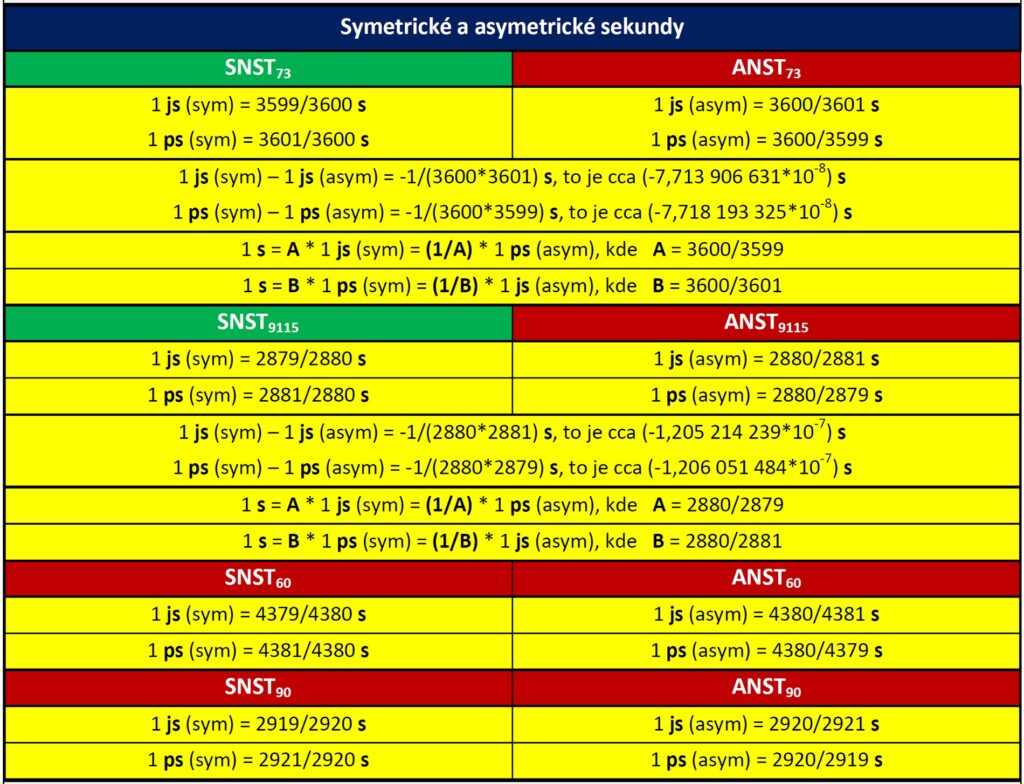
Rozdíl mezi symetrickými a asymetrickými veličinami je velmi malý. Je to řádově asi 10^-7 s. Asymetrická sekunda je vždy větší než její příslušná symetrická varianta. Platí to pro jarní i podzimní sekundu.

5.2 Shoda časů a maximální odchylky mezi SNST₇₃ a ANST₇₃

Obrázek ukazuje principiální schéma. Pokud je obrat SNST₇₃ na ose x vzdálen od středu obrázku o 73 min doleva, tak platí ∆x/x = 73*60/(182,5*24*3600) = 1/3600 a 1 mm ∆x na obrázku znamená 3,6 m x. Aby byl vidět detail, musí být na obrázku ∆x cca 1 cm. Polovina obrázku by potom byla dlouhá 36 m a celý obrázek až 72 m. Stejný princip platí i pro svislý směr a posun hodin o 73 jm u ANST₇₃.

Jak je vidět nejen z obrázku, ale i z výpočtů, čím větší je sekunda, tím menší počet sekund je potřebný na daný časový interval, tj. tím menší bude pro danou událost hodnota na ukazateli času (na ose y). Asymetrická sekunda je větší než symetrická, takže pro daný časový bod bude příslušný počet asymetrických sekund menší než symetrických (s výjimkou oblasti Y₁, Y₃). Z obrázku je také vidět, že věc symetrická z jednoho hlediska je asymetrická z jiného a opačně.

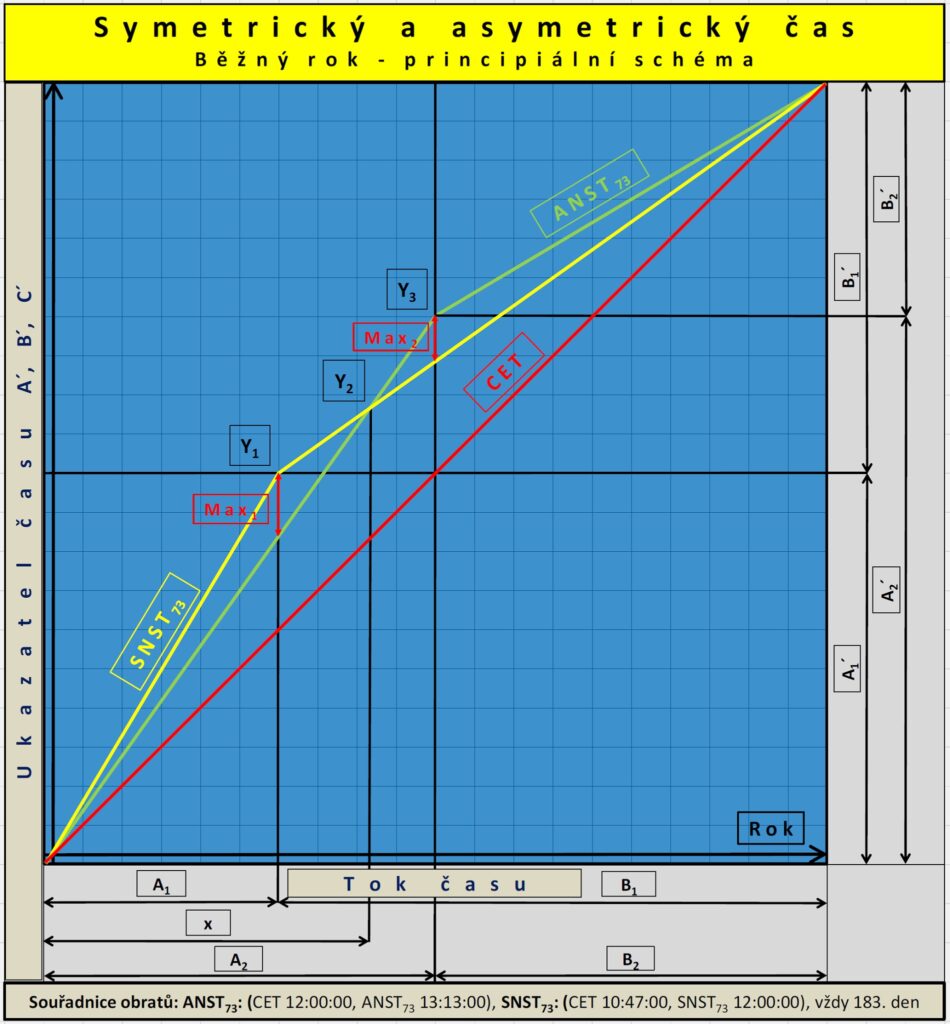
Administrativní a strojové jednotky času na grafu

Graf ukazuje, že na ose y tikají jak „administrativní (občanské)“ jednotky času s variabilní délkou časových intervalů, tak strojový čas se stejnou délkou časových intervalů. Na ose x probíhá „neviditelný“ tok času, který musíme nějakým procesem nejdříve „namapovat“ a čas „zviditelnit“.

Rovnice a hodnoty pro běžný rok (365 dní)

SNST₇₃ a posun o 73 běžných minut

Maximální počet symetrických js_s: A₁´ = 15 768 000                        1 js_s = 3599/3600 s
Maximální počet symetrických ps_s: B₁´ = 15 768 000                       1 ps_s = 3601/3600 s
CET souřadnice obratu v sekundách: A₁ = 15 763 620

SNST₇₃ [ss] = A_s´ + B_s´ = A/(1 js_s) + B/(1 ps_s) = A * 3600/3599 + B * 3600/3601

A, B je počet běžných sekund, A_s´, B_s´ je počet js_s a ps_s pro daný okamžik.

ANST₇₃ a posun o 73 jarních minut

Maximální počet asymetrických js_a: A₂´ = 15 772 380                       1 js_a = 3600/3601 s
Maximální počet asymetrických ps_a: B₂´ = 15 763 620                      1 ps_a = 3600/3599 s
CET souřadnice obratu v sekundách: A₂ = 15 768 000

ANST₇₃ [ss] = A_a´ + B_a´ = A/(1 js_a) + B/(1 ps_a) = A * 3601/3600 + B * 3599/3600

A, B je počet běžných sekund, A_a´, B_a´ je počet js_a a ps_a pro daný okamžik.

Rok = 31 536 000 s, půlrok = 15 768 000 s

Bod Y₁

První dvě časové souřadnice (CET a SNST) byly spočtené už dříve. Pro ANST₇₃ platí:

ANST₇₃ [ss_a] = A * 3601/3600 = A₁ * 3601/3600 = 15 767 998,783 (3 period) [js_a]

Maximální rozdíl mezi ukazatelem času na SNST hodinách a ANST hodinách je cca 1,2 „s“ (ss_s, ss_a).

Bod Y₃

Dvě souřadnice (CET a ANST) byly spočtené už dříve. Pro SNST₇₃ platí:

SNST₇₃ [ss_s] = A_s´ + B_s´ = A₁´ + B_s´ = A₁´ + B * 3600/3601 = A₁´ + (A₂ – A₁) * 3600/3601 =
15 772 378,783 671 202 444 [ss_s]

Maximální rozdíl mezi ukazatelem času na SNST hodinách a ANST hodinách je cca 1,2 „s“ (ss_s, ss_a).

Výpočet souřadnice x pro bod Y₂

CET [s] = x [s]
ANST₇₃ [ss_a] = A_a´ = A * 3601/3600 = x * 3601/3600
SNST₇₃ [ss_s] = A_s´ + B_s´ = A₁´ + (x – A₁) * 3600/3601

Rovnice pro bod Y₂

ANST₇₃ [ss_a] (x) = SNST₇₃ [ss_s] (x)
x * 3601/3600 = A₁´ + (x – A₁) * 3600/3601
x * (3601/3600 – 3600/3601) = A₁´ – A₁ * 3600/3601
x * 7201/(3600 * 3601) = A₁´ – A₁ * 3600/3601
x = (A₁´ * 3601 * 3600 – A₁ * 3600²)/7201

Když porovnáme všechny hodnoty, tak 183. den (v polovině roku) dojde v 11:47:00 CET k tomu, že ANST₇₃ se bude asi o 1,2 „s“ (ss_a) opožďovat za SNST₇₃ a ve 12:00:00 CET se naopak SNST₇₃ bude o 1,2 „s“ (ss_s)opožďovat za ANST₇₃. Vzhledem k tomu, že se jedná o maximální odchylky, symetrický a asymetrický čas se liší jen velmi málo. Druhé maximum je nepatrně menší.

Mezi těmito časy dochází ke shodě. Setkání časů nastává v 11:23:30 dle CET, kdy ANST₇₃ a SNST₇₃ ukazují stejný čas 12:36:29,7. První čas je v asymetrických jednotkách a druhý v symetrických.

5.3 Shoda časů a maximální odchylky mezi SNST₉₁₁₅ a ANST₉₁₁₅ 

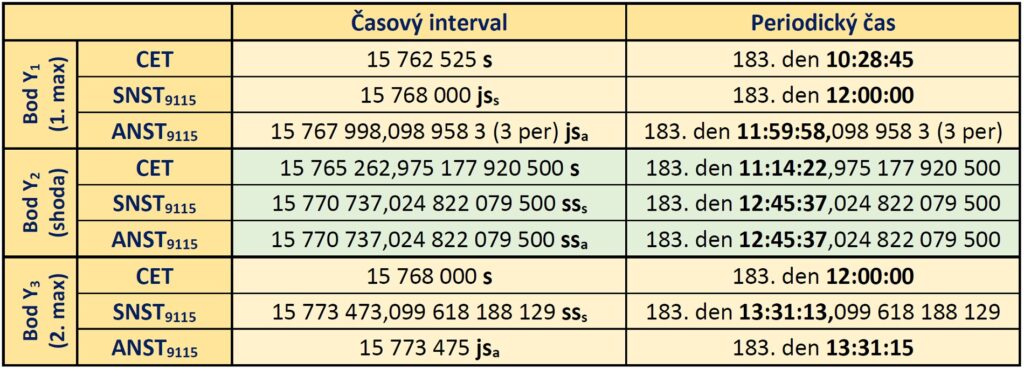
Když porovnáme tabulkové hodnoty, tak 183. den (v polovině roku) dojde v 10:28:45 CET k tomu, že ANST₉₁₁₅ se bude asi o cca 1,9 „s“ (ss_a) opožďovat za SNST₉₁₁₅ a ve 12:00:00 CET se naopak SNST₉₁₁₅ bude opožďovat o 1,9 „s“ (ss_s) za ANST₉₁₁₅. Vzhledem k tomu, že se jedná o maximální odchylky, symetrický a asymetrický čas se liší jen velmi málo. Druhé maximum je nepatrně menší.

Mezi těmito časy dochází ke shodě. Setkání časů nastane v cca 11:14:23 dle CET, kdy ANST₇₃ a SNST₇₃ ukazují stejný čas cca 12:45:37. První čas je v asymetrických jednotkách a druhý v symetrických.

5.4 Symetrie a asymetrie časových systémů

SNST

Předchozí graf ukazuje způsob konstrukce časových systémů. Pro SNST je zachována symetrie v počtu krátkých a dlouhých jednotek času. Je to symetrie kolem vodorovné osy (y = A₁´). Počet js je stejný jako počet ps (A₁´= B₁´). Počet CET jednotek času je vzhledem k bodu obratu asymetrický (A₁ ≠ B₁), ale protože CET sekundy jsou stále stejně dlouhé, tento druh asymetrie nevadí.

Vodorovný posun obratu doleva od středu je vlastně vzájemný posun SNST času vůči CET času ve strojových CET jednotkách. Tento posun je značený jako parametr P. Pokud se konec první části lomené křivky SNST posune vodorovně o P jednotek doleva, konec druhé části lomené křivky se posune o stejnou část doprava. Srovnáváme to s přímkou y = 1x, zde jí reprezentuje CET čas. Jde o „zákon, pravidlo“ zachování počtu CET jednotek v roce.

Směrnice křivek SNST

SNST₇₃ [ss] = A´+ B´ = A (s) * 3600/3599 + B (s) * 3600/3601,        k₁ = 3600/3599,        k₂ = 3600/3601
SNST₉₁₁₅ [ss] = A´+ B´ = A (s) * 2880/2879 + B (s) * 2880/2881,    k₁ = 2880/2879,        k₂ = 2880/2881

ANST

Pro ANST je zachována symetrie kolem svislé osy (x = A₂), počet strojových CET jednotek času do obratu a po obratu je stejný (A₂ = B₂). Tím vznikne rozdílný počet jarních a podzimních jednotek času (A₂´≠ B₂´). Jednotky jsou navíc asymetrické i navzájem svojí délkou vůči běžné sekundě. Tento druh asymetrie způsobuje mnohem větší složitost úvah o průběhu času a při výpočtech působí další komplikace. Posun obratu na svislé ose je posun ANST času vůči CET času v ANST jednotkách, konkrétně v jarních sekundách. Pro ANST jednotky bude posun značen jako parametr P´.

Pokud se konec první části lomené křivky posune svisle o P´ jednotek nahoru, konec druhé části lomené křivky se posune o stejnou část dolů. Opět srovnáváme s přímkou y = 1x, zde jí reprezentuje CET čas. Znovu jde o „zákon, pravidlo“ zachování počtu ANST jednotek v roce.

Směrnice křivek ANST

ANST₇₃ [ss] = A´+ B´= A (s) * 3601/3600 + B (s) * 3599/3600,        k₁ = 3601/3600,        k₂ = 3599/3600
ANST₉₁₁₅ [ss] = A´+ B´= A (s) * 2881/2880 + B (s) * 2879/2880,     k₁ = 2881/2800,        k₂ = 2879/2880

Přestupný rok

SNST

Zachování symetrie v přestupném roce znamená, že u SNST musíme zachovat symetrii podle vodorovné osy, tj. pro SNST₇₃₁₂ musíme vložit den o 24 hod kolem osy jako (12 jh + 12 ph)_SNST = (43 188 s + 43 212 s)_CET a pro SNST₉₁₃₀ vložíme (12 jh + 12 ph)_SNST = (43 185 s + 43 215 s)_CET. Zachová se tak symetrie vyžadovaná systémem SNST i celkový počet sekund a délka intervalu (1 js + 1 ps = 2 s).

ANST

U ANST je potřebné vložit 12 hod + 12 hod kolem svislé osy, proto jde o strojové CET jednotky. Na svislé ose to znamená, že ke 12 jh = 43 200 js patří dalších 12 js posunu v případě ANST₇₃, nebo 15 js v případě ANST₉₁₁₅. Tyto systémy proto můžeme v přestupném roce označit jako ANST₇₃₁₂ a ANST₉₁₃₀. Dále jsou uvedené přírůstky ANST souřadnic pro letní obrat oproti běžnému roku.

∆t ANST₇₃₁₂: 1 js = 3600/3601 s, 1s = 3601/3600 js, 12 hod = 43 200 * 3601/3600 js = 43 212 js
∆t ANST₉₁₃₀: 1 js = 2880/2881 s, 1s = 2881/2880 js, 12 hod = 43 200 * 2881/2880 js = 43 215 js

Vložení časového intervalu do ANST₇₃₁₂ znamená: (12 hod + 12 hod)_CET = (43 212 js + 43 188 ps)_ANST, pro ANST₉₁₃₀ to znamená: (12 hod + 12 hod)_CET = (43 215 js + 43 185 ps)_ANST. CET souřadnice vkládáme kolem svislé a ANST souřadnice kolem vodorovné osy, obrat je tu centrální bod a průsečík os.

5.5 Souřadné soustavy času

Běžné hodinky

Představme si dva majitele běžných hodinek. První má „přesné“ hodinky, protože jeho hodinky jdou dle CET a jsou neustále synchronizované s atomovými hodinami. Druhý má „nepřesné“ hodinky, protože jeho hodinky jdou napřed (nebo se opožďují). V nějakém okamžiku se oba podívají každý na svoje hodinky. Pan „přesný“ konstatuje, že je 8:40, pan „nepřesný“, že je 8:50. Protože oba vědí, že pan „přesný“ má hodinky synchronizované s atomovými hodinami, nehádají se a konstatují, že panu „nepřesnému“ jdou hodiny o 10 min napřed. Je to ale pravda?

Odpověď  není tak jednoduchá jak se zdá. Kdyby se ručičky na „nepřesných“ hodinách pohybovaly tak, aby jejich „10 min“ bylo opravdu 10 min dle atomových hodin, tak by nešly napřed, ale přesně. O kolik tedy vlastně jdou napřed? Těch „10 min“ na nepřesných hodinách by se teoreticky mohlo „natočit“ i za několik minut, pokud se hodiny budou točit dostatečně rychle.

Konstrukce rovnic typu ANST

Přesné hodinky necháme dojít na celou hodinu, počet jednotek času, o které jdou druhé nepřesné hodiny napřed je počet krátkých minut a sekund. U ANST to byly js (u „pomalých“ hodin ps). Jejich velikost zjistíme ze samostatných rovnic (zvlášť pro ty, co jdou rychleji v krátkých sekundách ks,  a zvlášť pro ty, co jdou pomaleji v dlouhých sekundách ds). Rovnice tady netvoří jeden měřící systém, týkají se různých hodin.

A [s] = (A + P_1A) [ks], pro hodiny, které jdou rychleji
A [s] = (A – P_1A) [ds], pro hodiny, které jdou pomaleji

Význam parametrů je stejný jako v předchozím textu s tím, že na začátku musí být hodinky synchronizované, musí mít společný počátek. Hodinky jdou o P₁ ks dopředu, nebo se o P₁ ds opožďují, protože A je souřadnice (číslo), které reprezentuje pro daný časový bod přesný čas a P_1A definuje vzájemný posun. Velikost ks a ds lze podle známých (a dříve popsaných) postupů dopočítat. Parametry A a P_1A jsou intervaly času a jsou to funkce času v různých časových jednotkách. P_1A je v ks nebo ds, A je někdy v „s“,a někdyv ks nebo ds.

Konstrukce rovnic typu SNST

Nepřesné hodinky necháme dojít na „celou“ hodinu, počet jednotek času, o které jdou druhé přesné hodiny pozadu je počet přesných minut a sekund. Jejich velikost zjistíme z rovnic:

(A – P_2S) [s] = A [ks], pro hodiny, které jdou rychleji
(A + P_2S) [s] = A [ds], pro hodiny, které jdou pomaleji

Význam parametrů je stejný jako dříve s tím, že na začátku musí být hodinky synchronizované. Paramery A, P_2S jsou intervaly času a jsou to funkce času. A je někdy v „s“ a někdy v ks nebo ds a P_2S je v „s“. Tady platí, že rychlé hodinky jdou o P_2S „s“ dopředu, nebo se o P_2S „s“ opožďují, protože P_2S je souřadnice (číslo), které reprezentuje pro daný časový bod posun časových souřadnic.

Proč je to někdy v sekundách a jindy v ks nebo ds?

Můžeme říci, že pokud čteme z ciferníku rychlých hodin, protože přesné máme nastavené na periodickou nulu (celou otočku), rozdíl je přímo v ks. Pokud čteme z přesných hodin, protože nepřesné máme nastavené na periodickou nulu, výsledek je v běžných minutách. Jenomže ciferníky jsou stejné a oboje hodiny si můžeme představit jako dvě dvojice ručiček, rychlých a pomalých na jednom ciferníku. Tak kdy odečítáme krátké sekundy a kdy přesné? Navíc tu odečítáme rozdíl dvou čísel na různých hodinách. Co s tím?

Jedná se o dvě různé časové soustavy. Pokud se díváme na přesné hodinky, tak jim bude trvat 10 min, než se dostanou z bodu 8:40 do bodu 8:50. Z pohledu nepřesných hodin se uvedený časový interval bude odehrávat 10 krátkých minut. Pokud by se točily opravdu rychle, těch 10 „min“ mohou „natočit“ i za několik běžných minut. Odpověď závisí na souřadné soustavě, ze které se na to díváme.

Časový posun je nejen relativní, ale není ani konstantní. Odpověď na otázku, o kolik jdou hodiny dopředu je závislá na čase, protože pokud hodiny jdou dopředu, tak to bude stále a rozdíl v časech se bude jen zvětšovat. V běžném životě je ale rozdíl v rychlostech hodin malý, a tak konstatování, že hodinky jdou o 10 min dopředu je většinou tolerovatelné pro všechny hodinky‚ přesné i nepřesné.

Rovnice pro přesné a nepřesné hodinky

Na obrázcích pro kostrukci SNST nebo ANST jsou výše uvedené rovnice konstruované buď pro k-cyklus, jednu celou otočku sekundové ručičky, nebo jako sumární pro intervaly A, P_1A,P_2S. V rámci této bilanční interpretace rovnice platí v celém časovém intervalu pro libovolný čas, tj. i pro všechny mezipolohy mimo dvě krajní (jednu pro konstrukci SNST a druhou pro konstrukci ANST). Konkrétní polohu ručiček určují proměnné intervaly času určené parametry hodin.

Rovnice je možné psát pro každý čas t a pro dvě časové souřadné soustavy.

Rovnice pro dvoje hodiny a časy 8:40 a 8:50

Z pohledu přesných hodin nastal čas A [s], rychlé hodiny jdou napřed a je na nich (A + 10*60) [ks].
A [s] = (A + 10*60) [ks] je rovnice pro časové souřadnice z pohledu přesných hodin, typ ANST.

Konstrukce rovnic typu ANST je vlastně konstrukce z pohledu časové souřadné soustavy základních referenčních hodin. Rozdíl v chodu hodin vychází v krátkých sekundách. Proto tyto rovnice také vznikly jako první.

Z pohledu rychlých hodin nastal čas A [ks], přesné hodiny se opožďují a je tam (A – 10*60) [s].
A [ks] = (A – 10*60) [s] je rovnice pro časové souřadnice z pohledu rychlých hodin, typ SNST.

Konstrukce rovnic typu SNST je konstrukce z pohledu souřadné soustavy nově konstruovaných atypických hodin, které považujeme za referenční. Časový posun tam vychází v sekundách.

Rovnice pro třetí pomalé hodiny a čas 8:27

Z pohledu přesných hodin nastal čas A [s], pomalé hodiny se opožďují a je na nich (A – 13*60) [ds].
A [s] = (A – 13*60) [ds] je rovnice pro časové souřadnice z pohledu přesných hodin, typ ANST.

Z pohledu pomalých hodin nastal čas A [ds], přesné jdou napřed a je tam (A + 13*60) [s].
A [ds] = (A + 13*60) [s] je rovnice pro časové souřadnicez pohledu pomalých hodin, typ SNST.

Velikost jednotek zjistíme už dříve popsaným způsobem. Je potřebné ale poznat společný počátek obou hodin, tj. bod, kdy nastala synchronizace časů, aby bylo možné určit délku intervalu A, na které  došlo k napředování nebo zpožďování hodin.

Můžeme mluvit o symetrických nebo asymetrických jednotkách času u běžných hodin?

Ne, protože symetrie a asymetrie se nastavují až vůči opačným jednotkám ve „společném měřícím systému“. U hodin, které jdou nejdříve dopředu vůči dlouhým, a u hodin, které jdou nejdříve pozadu vůči krátkým jednotkám.

Běžné hodinky, které jdou napřed, půjdou napřed pořád, ke shodě s přesným časem nedojde nikdy, protože se „rychlé“ hodiny nepřemění v půlce měřeného intervalu na „pomalé“. Stejné je to u hodin, které se opožďují. Zde je použitý pouze ANST a SNST postup konstrukce rovnic, který je u běžných hodin ekvivalentní. Pokud rovnice popisují jedny běžné hodiny, jsou navzájem transformovatelné.

Ekvivalentnost „SNST a ANST konstrukce“ rovnic pro běžné hodiny

Z pohledu rychlých hodin: (A – P_2S) [s] = A [ks], pro hodiny, které jdou rychleji
Z pohledu přesných hodin: (A + P_1A) [ks] = A [s], pro hodiny, které jdou rychleji

Rovnici „typu SNST“ algebraicky upravíme na „typ ANST“ přičtením výrazu P_2S. Rovnice budou stále popisovat stejný bod v čase t₀, ne časový vývoj, kde by se měnilo i A.

(A – P_2S) [s] = A [ks],
A [s] = A [ks] + P_2S [s], 1 s = k₁* ks, kde k₁ > 1,
A [s] = A [ks] + P_2S * k₁*ks, 
A [s] = (A + P_1A) [ks], kde P_1A = P_2S * k₁*ks, 
P_1A > P_2S

Rychlé hodiny jdou o P₁ krátkých sekund napřed (v původní rovnici se o P_2S „s“ zpožďovaly). U rovnic výše je důležité, že i když se jedná o parametry závislé na čase, úpravy rovnice jsou jen algebraické, pro jeden stejný čas t₀. Opačný postup je identický, viz rovnice v další kapitole.

Pokud máme stejný posun P_1A = P_2S, tak hodiny definované konstrukcí typu SNST pujdou rychleji než hodiny definované konstrukcí typu ANST a stejným parametrem (číslem). Jednotky ANST jsou vždy větší než ekvivalentní jednotky SNST, proto hodiny typu ANST tikají pomaleji. Platí to pro ks i ds.

Například u dříve použitého k-cyklu pro SNST₇₃ (3 600 s ± 1 s), pokud vyjdeme z SNST konstrukce pro rychlé hodiny (celá a celá – 1 s) budou dvě sekundové ručičky za další 1 s přibližně v „pozici ANST“ (celá a celá + „1 s“), ale ta rychlejší ručička bude o trochu dál než na 1 „s“, protože rychlé hodinky se k rozdílu jednoho dílku dopracovaly už o 1 s dříve, a tak za další 1 s udělají rychlé hodinky 1 ks (1 dílek) + něco navíc.

Dvěma různými typy rovnic se stejně velkými parametry (P_1A = P_2S) definujeme dvoje různě rychlé hodiny (rychlejší SNST a pomalejší ANST). Pokud dvěma rovnicemi chceme definovat jedny stejné hodiny, musí platit: P_1A > P_2S, jak bylo i vypočteno. Menší P_2S „SNST konstrukci“ chodu hodin zpomalí.

5.6 Netransformovatelnost symetrických a asymetrických systémů

Postup z předchozí kapitoly pro běžné hodiny by mohl vyvolat oprávněný dojem, že symetrické a asymetrické systémy jsou vzájemně převeditelné. To ale není pravda. Běžné hodiny (rychlé nebo pomalé) netvoří symetrický ani asymetrický měřící systém, proto je transformace možná. V dalších úpravách rovnic je ukázáno, proč rovnice dvou systémů nejsou navzájem transformovatelné.

Opět je i zde důležité, že úpravy rovnic jsou jen algebraické úpravy pro jeden stejný čas t₀.

ANST → SNST

Pro ks:
A [s] = (A + P_1A) [ks],
A [s] – P_1A [ks] = A [ks], 1 ks = k₁*s, k₁ < 1,
A [s] – P_1A* k₁*s = A [ks],
(A – P_2S) [s] = A [ks], kde P_2S [s] = P_1A* k_{1 *}s,
P_2S < P_1A

Pro ds:
A [s] = (A – P_1A) [ds],
A [s] + P_1A [ds] = A [ds], 1 ds = k₂*s, k₂ > 1,
A [s] + P_1A* k₂*s = A [ds],
(A + P_2S) [s] = A [ds], kde P_2S [s] = P_1A* k_{2 *}s,
P_2S > P_1A

Nejsou to rovnice pro systém SNST, protože P_2S z rovnice pro ks není totožné s P_2S z rovnice pro ds.
(A – P_2S) [s] = A [ks],
(A + P_2S^´) [s] = A [ds],
P_2S^´ ≠ P_2S

Důležité pravidlo (zákon) zachování počtu administrativních jednotek v roce by neplatil. Stejný výsledek dostaneme i při opačném postupu.

SNST → ANST

Pro ks:
(A – P_2S) [s] = A [ks],
A [s] = A [ks] + P_2S [s], 1 s = k₁*ks, k₁ > 1,
A [s] = A [ks] + P_2S* k₁*ks,
 A [s] = (A + P_1A) [ks], kde P_1A = P_2S* k₁*ks,
P_1A > P_2S

Pro ds:
(A + P_2S) [s] = A [ds],
A [s] = A [ds] – P_2S [s], 1 s = k₂*ds, k₂ < 1,
A [s] = A [ds] – P_2S* k₂*ds,
A [s] = (A – P_1A) [ds], kde P_1A = P_2S* k₂*ds,
P_1A < P_2S

Nejsou to rovnice pro systém ANST, protože P_1A z rovnice pro ks není totožné s P_1A z rovnice pro ds.
A [s] = (A + P_1A) [ks],
A [s] = (A – P_1A^´) [ds]
P_1A ≠ P_1A^´

Důležité pravidlo (zákon) zachování počtu administrativních jednotek v roce by neplatil.

Symetrické a asymetrické systémy nejsou navzájem transformovatelné. Z obrázku „Symetrický a asymetrický čas“ v kapitole 5.2 je důvod jasný stejně jako příčina, proč je to u běžných hodin možné.

5.7 Celočíselnost řešení pro běžný a přestupný rok

Celočíselný počet sekund v roce

A₀ [s] = (A₀ + P´) [js]
A₀ [s] = (A₀ – P´) [ps]

Jak je vidět z rovnic pro bod obratu, v případě asymetrického času bude počet jarních a podzimních sekund celočíselný pouze tehdy, pokud bude celkové posunutí času (hodin) P´ celočíselné.

A₀ [js] = (A₀ – P) [s]
A₀ [ps] = (A₀ + P) [s]

U symetrického času by posun P mohl být teoreticky i neceločíselný a počet js, ps i běžných sekund v roce by zůstal celočíselný (s neceločíselným obratem v sekundách).

Je celočíselný počet sekund v roce nutný?

Pro zachování přehledného časového a kalendářního systému musí být počet běžných i variabilních sekund (js i ps) v roce vždy celočíselný. Všechny rovnice pro NST tuto podmínku pro běžný rok o 365 dnech splňují automaticky pro celočíselný časový posun. Pro SNST je to splněno vždy, pro každé P.

Pro body obratu je také lepší, ale už ne nutné, aby obrat nastal na konci jedné a na začátku druhé sekundy, běžné i variabilní. Hodiny jsou stroj a nejlepší je měnit variabilní sekundu na konci jedné a na začátku druhé sekundy, běžné i variabilní. Pro rok o 365 dnech je to za výše uvedených podmínek splněno. Pro přestupný rok o 366 dnech tato další podmínka omezuje počet možných řešení.

SNST

Musí platit: 1 js*12*60*60 je v sekundách celé číslo a zároveň 1 ps*12*60*60 je v sekundách celé číslo. Obě výše uvedené podmínky vyplývají z řešení přestupného roku (vkládání časového intervalu). Z tohoto důvodu v tabulkách ani grafech není zvažována křivka SNST₆₀ (posun o 60 min přesně) ani SNST₉₀ (posun o 90 min přesně). Ani jedna z křivek není vhodná pro přestupný rok, protože obrat u nich nenastane pro celočíselný násobek běžných sekund, ale jen variabilních sekund. Křivky uvedené v tabulkách a grafech, na které odkazuje začátek tohoto článku, podmínky celočíselného řešení splňují.

ANST

Jak je vidět z kapitoly 5.4, pro ANST₇₃₁₂ a ANST₉₁₃₀, celočíselná řešení existují nejen v běžném roce (365 dní), ale i v přestupném roce (366 dní). Řešení mají do obratu i po obratu celočíselný počet sekund (js, ps i běžných sekund). Asymetrické křivky proto můžeme alespoň teoreticky použít také pro běžný i přestupný rok.

6. Další posuny času a vyrovnávání rozdílů mezi UTC a UT1

6.1 Používané značky, zkratky a úvod do problematiky

GMT – Greenwich Mean Time – Greenwichský střední čas založený na rotaci Země.
UT – Universal Time – světový čas založený na rotaci Země, obecnější pojem než GMT.
UT0 – to je GMT, solární čas pozorovaný na jakémkoliv místě na Zemi přepočtený na nultý poledník.
UT1 – je upřesněním UT0, zohledňuje pohyb osy rotace Země.
UT2 – upřesněné UT1, započteny ještě sezónní změny rychlosti rotace Země.
UTC – Coordinated Universal Time – koordinovaný světový čas založený na atomových hodinách, UTC je od roku 1972 korigován podle UT1 (UTC – UT1 < 0,9 s). UTC+1 a UTC+2 je „zimní“ a letní čas v ČR.
TAI – International Atomic Time (TAI), čas podle atomových hodin, od UTC se liší o vložené sekundy (UTC +37 s = TAI ke dni 30. 3. 2020).

Vznik pojmů UT a UTC. Pojem UT (Universal Time) vznikal už v devatenáctém století jako protipól k místnímu času. Měl reprezentovat obecnost a univerzalitu a nebyl exaktně definován. V devatenáctém století se používal spíše pojem GMT (Greenwich Mean Time), dnes všeobecně známý pojem pro měření času na základě polohy Slunce na nultém poledníku.

Až v roce 1928 IAU (International Astronomical Union) doporučila používat název „Universal Time“ jako náhradu za GMT i GCT (Greenwich Civil Time). GMT se měřil od jednoho poledne do druhého a GCT naopak od půlnoci. Tak vznikla v roce 1928 vlastně první exaktní definice UT. Čas se podle UT začal jednoznačně měřit od půlnoci do půlnoci jako dnes.

Ve čtyřicátých letech se k vysílání časových signálů začaly používat krystalické hodiny – quartz crystal clock a v padesátých letech atomové hodiny. Protože čas závisel nejdříve na kmitech krystalu a později na frekvenci přechodu energetických hladin atomu Cézia, začal se oddělovat od astronomie a musel se korigovat s rotací Země.

Korekce na skutečnou rotaci Země se prováděla nejdříve na UT2 vkládáním úseků menších než 1 s, ale protože se časové skoky (time steps) v technice neosvědčily, po roce 1972 se čas začal korigovat na UT1 vkládáním celých sekund (leap second).

V roce 1959 se zjistilo, že různé země vysílají různé navzájem nekoordinované signály. Proto se několik významných světových laboratoří dohodlo na vzájemné koordinaci časových signálů založených na atomových hodinách a UT. Tak začala spolupráce mnoha laboratoří ve světě na měření „atomového“ času. Koordinace začala 1. 1. 1960 a pro takto měřený čas (na základě atomových hodin a korigovaných dle UT) se začal používat název UTC – Coordinated Universal Time.

V současnosti UTC plně nahradil původní „solární čas“ na celém světě a stal se mezinárodním standardem pro měření času. Podobně jako GMT používá také časová pásma (UTC+1, UTC+2…) a v běžné mluvě se s ním někdy zaměňuje, i když GMT se nerovná UTC.

6.2 Přestupná sekunda

V současné době je čas, který využívá periodický děj – otáčení Země kolem své osy (UT1), zpřesněn a zdokonalen jiným časem (TAI) založeným na periodickém procesu, který probíhá v atomu, a který je mnohem stabilnější než rotace Země. Tento čas je měřen podle tzv. atomových hodin a přesnost se tam blíží k dokonalosti. Koneckonců Země je jen „velká brambora“, která se otáčí kolem své osy a působí na ni další kosmické síly, které mají na otáčení a tím i přesnost periodického děje vliv.

UTC je čas, jehož jednotky nezávisí na rotaci Země, ale jen na atomových hodinách. UTC je kombinací atomových hodin a korekce podle UT1, protože i UTC chceme svázat s rotací naší planety a nechceme, aby se tento čas od skutečného dne úplně „utrhl“. Aby se UTC a UT1 nerozcházely (UTC tiká trochu rychleji než UT1), vkládá se do UTC občas (např. v letech 2005, 2008, 2012, 2015, 2016) jedna sekunda, aby odchylka UTC od UT1, který reprezentuje skutečnou rotaci Země kolem své osy, byla menší než 1 sekunda.

Rotace Země se zpomaluje, proto přesných časových jednotek potřebných na synchronizaci UTC s rotací bude třeba dlouhodobě stále víc (teď stačí 1 sekunda na několik let). Sekunda se vkládá tak, že v případě potřeby na Silvestra (nebo 30. června) po čase 23:59:59 následuje ještě 23:59:60, a až pak 00:00:00 jako začátek nového dne. Přes zdánlivou podobnost UTC není GMT, UTC jsou tikající atomové hodiny (s občasnou korekcí).

V posledních letech (2023) se mluví také o opačném vlivu urychlování rotace Země, pravděpodobně vlivem změny momentu setrvačnosti v důsledku přeskupování hmot na naší planetě. To může být způsobeno zemětřeseními nebo i jako důsledek oteplování (tání ledovců) atd. V budoucnosti by se proto mohlo stát, že se „vložená sekunda“ bude naopak ubírat.

6.3 Co je zdrojem nesouladu mezi UTC a UT1

Otočení Země kolem své osy trvá v současnosti asi 86 400,002 s místo správných 86 400 s. Nejedná se tu o žádný konkrétní den, ale o střední den měřený vůči Slunci. Nesoulad délky dne znamená, že každých 500 dní, tj. cca každých 1,5 roku je potřebné vkládat 1 přestupnou sekundu. Proč to vědci neudělali pořádně, aby UTC bylo v souladu s UT1? Kde se tento šlendrián vzal? Dá se to spravit?

Složky nestability rotace Země

Už poměrně dávno se zjistilo, že rotace Země není stabilní a mění se jednak ze dne na den z hlediska otáčení vůči Slunci, a jednak dlouhodobě. Prvním zdrojem nestability je měření rotace vůči Slunci. Sluneční den by byl nestabilní, i kdyby byla rotace setrvačníku absolutně stabilní. Nestabilitu tam vnáší pohyb Země kolem Slunce, nerovnoměrná rychlost pohybu i geometrie elipsy a její sklon. Sekunda byla proto definována jako 1/86 400 část středního slunečního dne, ne běžného dne.

Druhým zdrojem jsou dlouhodobé změny rotace Země jako setrvačníku. Nejvýznamnější je vliv Měsíce, který zpomaluje otáčení Země kolem své osy. Zpomalování důsledkem slapových sil je asi 0,0023 s za století (zpomalení na 1 otočení Země). Důvodů pro nestabilní rotaci je ale víc.

Rotace se mění také tím, že se mění rozložení hmoty setrvačníku. Významnou složkou je například tání ledovců. Voda ze severního a jižního pólu odtéká a půda se zvedá, protože tlak ledovců na povrch Země klesá. Hmota se jakoby přesouvá víc k severu a rozložení hmoty setrvačníku se mění.

Důsledkem je naopak mírné zrychlování rotace a zkrácení délky dne o 0,6 ms/století. Dále ke změně rotace přispívají jakékoliv přesuny hmot v souvislosti s ročními obdobími nebo jinými vlivy. Celkově je rotace Země zpomalována a den se prodlužuje o 0,0017 s/století (0,0023 – 0, 0006).

Bylo proto nutné hledat jiné stabilnější periodické děje. Mezikrokem bylo vynalezení hodin řízených kmity krystalu, ale po vynálezu céziových atomových hodin v roce 1955 se ukázalo, že čas se dá měřit ještě mnohem přesněji. Právě na základě těchto hodin vznikla v roce 1967 nová definice „atomové“ sekundy jako násobku period záření atomu Cézia.

Přechodem mezi stejnými energetickými hladinami dochází k vyzáření vždy stejné frekvence záření a počet cyklů (period) tohoto vyzařování definuje novou „atomovou“ sekundu. 1 s = 9 192 631 770 period záření mezi přesně definovanými hladinami atomu Cézia. Takový čas už nezávisí na rotaci Země a kalibrační zdroj časomíry je použitelný všude: na zemi, ve vzduchu i v kosmu. Periodický děj poskytuje neskutečnou přesnost. K odchylkám o 1 s dochází v řádu milionů až desítek milionů let.

Aby bylo možné nastavit počet cyklů záření, musela se nejdříve vzít nějaká rozumná délka sekundy, na kterou se to „naroubovalo“. Stará a nová sekunda se musely nějak „sešít“. Udělalo se to tak, že se vzal rok 1900 a z něj se odvodila délka sekundy jako 1/86 400 část středního slunečního dne. Potom se definoval počet cyklů vyzařování tak, aby jejich celková doba byla s takto definovanou délkou sekundy shodná.

Problém je v tom, že je těžké napasovat něco, co je stabilní na něco, co se mění jak krátkodobě, tak dlouhodobě, a tak se od roku 1900 doba rotace Země změnila z původních 86 400 s až na současných 86 400,002 s. Když se v šedesátých letech minulého století ve většině zemí zavedl UTC jako časový standard, bylo nutné začít vkládat přestupnou sekundu, aby nedocházelo k rozcházení mezi „atomovým“ časem a slunečním. V současnosti existují i názory, že by se vkládání přestupné sekundy mělo zrušit, protože vkládání sekund působí v technice problémy.

6.4 Přestupná sekunda a SNST₇₃ nebo SNST₉₁₁₅

Úloha zní: vložit do SNST₇₃ přestupnou sekundu z důvodu zpomalování rotace Země. Jak to udělat? Provedeme jednoduché posunutí „obratu“ o půl sluneční hodiny, tj. v přestupném roce už na 23:30:00 místo 24:00:00 dle SNST a v běžném roce na 11:30 místo 12:00:00 dle SNST. Výsledkem bude posunutí o potřebnou sekundu.

Pokud posuneme uvedeným způsobem „obrat“, pro součet času za celý rok v běžných jednotkách bude platit následující:

(182,5 jd – 30 jm) + (182,5 pd + 30 pm) = 365 dní + (30 pm – 30 jm) = 365 dní + 30*60* (1 ps – 1 js) = 365 dní + 30*60*((1 + Δt) – ( 1 – Δt)) s = 365 dní + 60*60*Δt s = 365 dní + 1 s

Δt = 1/3600 s

Touto velmi jednoduchou „operací“ je možné do daného kalendářního roku s přirozeným slunečním časem vložit 1 běžnou sekundu, aniž by se celkový počet slunečních sekund v daném roce změnil. Žádná přestupná sekunda, která by narušovala počet sekund v roce, se do NST vkládat nemusí. Pro SNST₉₁₁₅ by se obrat musel posunout o 24 jm (Δt = 1/2880 s).

6.5 Jaký nejmenší čas je možné vkládat do SNST₇₃ a SNST₉₁₁₅?

Princip variabilního mapování času umožňuje velmi elegantní posouvání času a vkládání libovolných časových úseků i mnohem kratších, než je 1 sekunda. Nejmenší jednotkou, o kterou je možné posunout obrat je 1 js (viz poznámka) ve směru nebo proti směru hodinových ručiček (tj. dopředu nebo dozadu).

Celkový počet slunečních sekund v průběhu roku musí být zachován a celočíselný (86 400 denně x 365 resp. 366 dní v roce). Kolik jarních sekund se přidá, tolik podzimních sekund se musí ubrat (a opačně). Posun obratu o 1 sekundu znamená buď o 1 js víc a o 1 ps míň nebo opačně.

Pozn.: Z pohledu času probíhajícího od začátku roku můžeme říci, že „obrat“ posuneme o 1 js doprava nebo doleva. Z pohledu druhého „půl roku“ by se dalo říci, že „obrat“ posouváme naopak o 1 ps doleva nebo doprava. Vypadá to jako rozpor, ale není. Výsledek je v obou případech stejný, protože se jednotky navzájem vymění a celkový časový posun je jejich vzájemný rozdíl, který se touto úvahou nezmění. Je proto jedno jak to popíšeme.

Čas, který uběhne za rok při posunutí obratu o 1 sluneční sekundu

• Obrat posuneme o 1 sluneční sekundu zpět (proti směru hodinových ručiček), tj. rok bude mít o 1 js méně a místo ní o 1 ps více (celkový počet slunečních sekund v roce bude stejný)

(182,5 jd – 1 js) + (182,5 pd + 1 ps) = 365 dní + (1 ps – 1 js) = 365 dní + ((1 + Δt) – (1 – Δt)) s = 365 dní + 2*Δt s = 365 dní + 2/3600 s. V tomto případě se rok o (2/3600) sekundy prodlouží.

• Obrat posuneme o 1 „sluneční sekundu“ dopředu (ve směru hodinových ručiček), tj. rok bude mít o 1 js více a 1 ps méně (celkový počet slunečních sekund v roce bude opět stejný)

(182,5 jd + 1 js) + (182,5 pd – 1 ps) = 365 dní + (1 js – 1 ps) = 365 dní + ((1 – Δt) – (1+Δt)) s = 365 dní – 2*Δt s = 365 dní – 2/3600 s. V tomto případě se rok o (2/3600) sekundy zkrátí.

To samé ještě jinak: 2 sekundy, na které by se změnila 1 js + 1 ps nahradíme buď dvakrát js, nebo dvakrát ps.

2 js – 2 s = (2*(1 – Δt) – 2) s = -2*Δt s (rok se o 2/3600 sekundy zkrátí)
2 ps – 2 s = (2*(1 + Δt) – 2) s = 2*Δt s (rok se o 2/3600 sekundy prodlouží)

Nejmenší čas, který je možné vkládat do UTC je 1 běžná „vložená“ sekunda (pokud nechceme vkládat zlomek časové jednotky) a počet administrativních jednotek času v jednom kalendářním roce se tím změní. Rok má o 1 sekundu víc.

Nejmenší čas, který je možné vkládat do SNST₇₃ (nebo odečítat) je 5,5 (5 „periodických“) * 10^-4 sekundy. Pro SNST₉₁₁₅ je to 6,94 (4 „periodické“) * 10^-4 sekundy. Počet administrativních jednotek času v jednom kalendářním roce se tím nezmění. Rok nemá ani o 1 administrativní sekundu víc, přesto je o 1 sekundu delší.

6.6 Vkládání a vynechávání časových intervalů v rámci SNST obecně

Vzhledem k symetrii slunečních jednotek platí vždy, že součet „stejné“ jarní a podzimní jednotky času (sluneční sekundy, minuty, hodiny a dne) je 2x běžná jednotka času (sekunda, minuta, hodina a den). Naopak rozdíl „stejných“ jednotek bude vždy 2*Δt, kde Δt je odchylka dané konkrétní sluneční jednotky od běžné časové jednotky stejné „velikosti“, stejného „řádu“ (hodiny, minuty, sekundy).

Například: 1 jh + 1 ph = ((1 hod – Δt_hod) + (1 hod + Δt_hod)) = 2 hod
                    1 jh – 1 ph = ((1 hod – Δt_hod) – (1 hod + Δt_hod)) = -2*Δt_hod = -2 s

Dva příklady pro SNST₇₃: Posun obratu o 10 dní dříve by znamenal vložení 8 běžných minut (z tabulky 10*48/60) do kalendářního roku, aniž by se musel měnit počet administrativních sekund v daném roce. Posun obratu o 5 hodin později by znamenal zkrácení roku o 10 běžných sekund (z tabulky 5*2).

6.7 Pružnost občanského (administrativního) času

Variabilní čas je pružný jako guma na trenýrkách. Pokud pevný (modrý) vodorovný pás reprezentuje tok času a naprostou pevnost a neměnnost časových cyklů (u jednotlivých po sobě následujících let), žluto-červená linie ukazuje, že administrativní jednotky je možné skládat různě a výsledkem je pružnost délky časového intervalu. Svislá osa znázorňuje předcházení nebo opožďování hodin včetně symbolického počtu dvou (ilustračních) administrativních jednotek na ukazateli času.

Při prvním způsobu (schéma 2+2) jdou hodiny nejdříve napřed (o 2 administrativní jednotky času), pak se o stejné 2 jednotky času vrátí, křivky se protnou a časy se shodují jak počtem časových jednotek, tak délkou časového intervalu.

Při druhém způsobu se skládají jednotky jako (3+1), tři krátké a jedna dlouhá. Časový interval je potom kratší při stejném počtu uběhlých administrativních sekund. Po uzavření časového cyklu (1 roku) jdou hodinky ve srovnání se SEČ napřed. Časové systémy se v zimním bodě obratu nesetkají (neukazují stejný čas).

Ve třetí variantě se skládá kombinace 1+3 (jedna krátká a tři dlouhé). Výsledkem je delší časový interval a stejný počet administrativních jednotek času. Po uzavření časového cyklu (1 roku) se hodinky ve srovnání se SEČ opožďují. Časové systémy se v zimním bodě obratu nesetkají (neukazují stejný čas).

Tento druh změn je z hlediska běžného uživatele času nepozorovatelný.

6.8 Celočíselnost a vkládání časových intervalů do ročního cyklu

6.8.1 Vložení nebo odebrání 1 sekundy

Jak bylo v kapitole 6.4 popsáno, v případě SNST₇₃ posun obratu doleva o 30 jm znamená vložení 1 s do ročního cyklu. V současnosti se tento postup občasného „přifouknutí roku“ používá na vyrovnávání rozdílu mezi UTC a UT. Stejný posun doprava by znamenal naopak odebrání 1 s. U SNST₉₁₁₅ na vložení 1 sekundy stačí posun obratu o 24 jm.

Rozdíl mezi novým a starým systémem je v tom, že vložení 1 s už neznamená administrativní změnu počtu sekund v roce, jak je to dnes. Sekunda se může vložit do variabilního času s využitím pružnosti časového systému s nezměněným počtem administrativních jednotek v roce.

Posun obratu doleva o 30 jm u SNST₇₃ znamená, že se obrat posune v CET o 30*60*3599/3600 = 3599*0,5 sekund doleva. Z hlediska celočíselnosti je to (1799 + 0,5) sekundy. U SNST₉₁₁₅ to bude 24*60*2879/2880, tj. (1439 + 0,5) sekundy. Jedná se o neceločíselný posun obratu v CET, který tu reprezentuje UTC (atomový čas).

U základních rovnic pro SNST se sčítají dva stejné půlroky a dochází k eliminaci dokonce i neceločíselného P v rámci roku:

A₀ [js] = (A₀ – P) [s] 
A₀ [ps] = (A₀ + P) [s]

V případě posunu obratu je situace složitější. Při posunu obratu směrem doleva v prvním jarním půlroku P´ js odebereme a ve druhém podzimním půlroku stejný počet P´ ps přidáme:

(A₀ – P´) [js] = (A₀ – P₁) [s] = (A₀ – P – ∆P₁) [s], kde P₁ = P + ∆P₁
(A₀ + P´) [ps] = (A₀ + P₂) [s] = (A₀ + P + ∆P₂) [s], kde P₂ = P + ∆P₂

Celkový sumární počet js a ps zůstane zachován. Na pravé straně se tím změní posun obratu v sekundách. Předpokládáme, že u první rovnice o ∆P₁ a u druhé rovnice o ∆P₂.

Parametr P jako člen rovnice odkazuje na původní konstrukci časového systému (před posunem obratu). Bilanční rovnice pro bod obratu jsou v tomto případě jiné než u základních rovnic pro konstrukci časového systému, ale zrychlení a zpomalení hodin chceme u časového systému zachovat. Hodiny půjdou stejně rychle nebo stejně pomalu jako předchozí, protože to musí být „stejné hodiny“ jen s posunutým obratem.

Zrychlení a zpomalení hodin u SNST
k [js] = (k – 1) [s] nebo jinak (ekvivalentně) A₀ [js] = (A₀ – P) [s] 
k [ps] = (k + 1) [s] nebo jinak (ekvivalentně) A₀ [ps] = (A₀ + P) [s]

V platnosti zůstává i vztah pro původní P jako počet k-cyklů tvořících půlrok: A₀ = P*k. Po dosazení vztahů pro zrychlení a zpomalení hodin do bilančních rovnic pro js a ps (nebo po přímém odečtení ekvivalentních vztahů vpravo) dostaneme:

js: P´[js] = ∆P₁ [s]
ps: P´[ps] = ∆P₂ [s]

Jarní a podzimní půlrok už nemají stejný počet administrativních sekund, symetrie SNST je částečně narušena.

Při posouvání obratu jedním nebo druhým směrem se vzhledem k nahrazení krátkých jednotek času dlouhými jedná o „operaci“ kompenzovanou u variabilních jednotek (jejich celkový počet se zachovává), ale „nekompenzovanou“ u CET jednotek (∆P₁ ≠ ∆P₂). Zákon, pravidlo zachování počtu CET jednotek času při takto formulovaných rovnicích už neplatí a časový interval je proto delší nebo kratší o rozdíl (∆P₂ – ∆P₁).

Je to vidět z rovnice: (A₀ – P´) [js] + (A₀ + P´) [ps] = (A₀ – P – ∆P₁) [s] + (A₀ + P + ∆P₂) [s] = (2*A₀ + (∆P₂ – ∆P₁)) [s].

6.8.2 Výsledky výpočtů pro vložení nebo odebrání 1 sekundy

Výpočty byly provedené na základě hodnot z kapitol 4.1 a 4.2.

SNST₇₃ a běžný rok

←

Letní obrat dle CET: 183. den v 10:17:00 (+0,5 s), od začátku roku je to 15 761 820,5 s.
Letní obrat dle SNST₇₃: 183. den v 11:30:00, od začátku roku je to 15 766 200 js.
Zimní obrat dle CET: 00:00:01, to je 31 536 001 s.
Zimní obrat dle SNST₇₃: 1. den roku v 00:00:00.
Prvý půlrok má 15 766 200 js, druhý půlrok má 15 769 800 ps.
SNST symetrie je částečně narušena. Sluneční rok zachovává 31 536 000 ss.

→

Letní obrat dle CET: 183. den v 11:16:59 (+0,5 s), od začátku roku je to 15 765 419,5 s.
Letní obrat dle SNST₇₃: 183. den v 12:30:00, od začátku roku je to 15 769 800 js.
Zimní obrat dle CET: 23:59:59, to je 31 535 999 s a 31.12.
Zimní obrat dle SNST₇₃: 1. den roku v 00:00:00.
Prvý půlrok má 15 769 800 js, druhý půlrok má 15 766 200 ps.
SNST symetrie je částečně narušena. Sluneční rok zachovává 31 536 000 ss.

SNST₉₁₁₅ a běžný rok

←

Letní obrat dle CET: 183. den v 10:04:45 (+0,5 s), od začátku roku je to 15 761 085,5 s.
Letní obrat dle SNST₉₁₁₅: 183. den v 11:36:00, od začátku roku je to 15 766 560 js.
Zimní obrat dle CET: 00:00:01, to je 31 536 001 s.
Zimní obrat dle SNST₉₁₁₅: 1. den roku v 00:00:00.
Prvý půlrok má 15 766 560 js, druhý půlrok má 15 769 440 ps.
SNST symetrie je částečně narušena. Sluneční rok zachovává 31 536 000 ss.

→

Letní obrat dle CET: 183. den v 10:52:44 (+0,5 s), od začátku roku je to 15 763 964,5 s.
Letní obrat dle SNST₉₁₁₅: 183. den v 12:24:00, od začátku roku je to 15 769 440 js.
Zimní obrat dle CET: 23:59:59, to je 31 535 999 s a 31.12.
Zimní obrat dle SNST₉₁₁₅: 1. den roku v 00:00:00.
Prvý půlrok má 15 769 440 js, druhý půlrok má 15 766 560 ps.
SNST symetrie je částečně narušena. Sluneční rok zachovává 31 536 000 ss.

SNST₇₃₁₂ a přestupný rok

←

Letní obrat dle CET: 183. den v 22:16:48 (+0,5 s), od začátku roku je to 15 805 008,5 s.
Letní obrat dle SNST₇₃₁₂: 183. den v 23:30:00, od začátku roku je to 15 809 400 js.
Zimní obrat dle CET: 00:00:01, to je 31 622 401 s.
Zimní obrat dle SNST₇₃₁₂: 1. den roku v 00:00:00.
Prvý půlrok má 15 809 400 js, druhý půlrok má 15 813 000 ps.
SNST symetrie je částečně narušena. Sluneční přestupný rok zachovává 31 622 400 ss.

→

Letní obrat dle CET: 183. den v 23:16:47 (+0,5 s), od začátku roku je to 15 808 607,5 s.
Letní obrat dle SNST₇₃₁₂: 184. den v 00:30:00, od začátku roku je to 15 813 000 js.
Zimní obrat dle CET: 23:59:59, to je 31 622 399 s a 31.12.
Zimní obrat dle SNST₇₃₁₂: 1. den roku v 00:00:00.
Prvý půlrok má 15 813 000 js, druhý půlrok má 15 809 400 ps.
SNST symetrie je částečně narušena. Sluneční přestupný rok zachovává 31 622 400 ss.

SNST₉₁₃₀ a přestupný rok

←

Letní obrat dle CET: 183. den v 22:04:30 (+0,5 s), od začátku roku je to 15 804 270,5 s.
Letní obrat dle SNST₉₁₃₀: 183. den v 23:36:00, od začátku roku je to 15 809 760 js.
Zimní obrat dle CET: 00:00:01, to je 31 622 401 s.
Zimní obrat dle SNST₉₁₃₀: 1. den roku v 00:00:00.
Prvý půlrok má 15 809 760 js, druhý půlrok má 15 812 640 ps.
SNST symetrie je částečně narušena. Sluneční přestupný rok zachovává 31 622 400 ss.

→

Letní obrat dle CET: 183. den v 22:52:29 (+0,5 s), od začátku roku je to 15 807 149,5 s.
Letní obrat dle SNST₉₁₃₀: 184. den v 00:24:00, od začátku roku je to 15 812 640 js.
Zimní obrat dle CET: 23:59:59, to je 31 622 399 s a 31.12.
Zimní obrat dle SNST₉₁₃₀: 1. den roku v 00:00:00.
Prvý půlrok má 15 812 640 js, druhý půlrok má 15 809 760 ps.
SNST symetrie je částečně narušena. Sluneční přestupný rok zachovává 31 622 400 ss.

6.8.3 Jiné (menší) vložené intervaly a celočíselnost

Vkládání malých časových intervalů už bylo posáno v kapitole 6.5. Variabilní mapování umožňuje vkládání extremně malých časových intervalů řádu 10^-4 s. Pro lepší manipulaci a přehlednost je ale možné „celočíselnost“ svázat například s desetinou sekundy.

Pokud posun obratu u SNST₇₃ o 30 jm doleva znamená vložení 1 s do ročního cyklu, pak 3 jm vloží do ročního intervalu 0,1 s. U SNST₉₁₁₅ 24 jm znamená 1 s, takže posun o 2,4 jm vloží 0,1 s.  

Posun obratu o 3 jm doleva u SNST₇₃ znamená, že se obrat v CET posune o 3*60*3599/3600 = 179,95 s doleva. U SNST₉₁₁₅ to bude 2,4*60*2879/2880, tj. 143,95 s. Jedná se o neceločíselný posun obratu v CET, který tu reprezentuje UTC (atomový čas). Posun obratu bude z hlediska celočíselnosti obsahovat vždy ½*zlomku intervalu posunu (pokud ten tvoří zlomek), v tomto případě ½*0,1 = 0,05. Je to vidět z následujících rovnic:

Posun obratu o 1 jednotku doleva znamená vložení intervalu: 1 ps – 1 js = 2*∆t, kde ∆t = 1s – 1 js
Posun obratu o n jednotek doleva znamená vložení intervalu: n*(1 ps – 1 js) = n*2*∆t
Posun obratu bude: n*js = n*(1 – ∆t) = n – n*∆t

Pokud označíme n*2*∆t jako x a bude se jednat o zlomek, například 0,1 s, tak posun obratu bude obsahovat zlomek ½*x, tj. 0,05 s.

6.8.4 Výsledky výpočtů pro vložení nebo odebrání 0,1 s

Výpočty byly provedené na základě hodnot z kapitol 4.1 a 4.2.

SNST₇₃ a běžný rok

←

Letní obrat dle CET: 183. den v 10:44:00 (+0,05 s), od začátku roku je to 15 763 440,05 s.
Letní obrat dle SNST₇₃: 183. den v 11:57:00, od začátku roku je to 15 767 820 js.
Zimní obrat dle CET: 00:00:00 (+0,1 s), to je 31 536 000,1 s.
Zimní obrat dle SNST₇₃: 1. den roku v 00:00:00.
Prvý půlrok má 15 767 820 js, druhý půlrok má 15 768 180 ps.
SNST symetrie je částečně narušena. Sluneční rok zachovává 31 536 000 ss.

→

Letní obrat dle CET: 183. den v 10:49:59 (+0,95 s), od začátku roku je to 15 763 799,95 s.
Letní obrat dle SNST₇₃: 183. den v 12:03:00, od začátku roku je to 15 768 180 js.
Zimní obrat dle CET: je 23:59:59 (+0,9 s), to je 31 535 999.9 s a 31.12.
Zimní obrat dle SNST₇₃: 1. den roku v 00:00:00.
Prvý půlrok má 15 768 180 js, druhý půlrok má 15 767 820 ps.
SNST symetrie je částečně narušena. Sluneční rok zachovává 31 536 000 ss.

SNST₉₁₁₅ a běžný rok

←

Letní obrat dle CET: 183. den v 10:26:21 (+0,05 s), od začátku roku je to 15 762 381,05 s.
Letní obrat dle SNST₉₁₁₅: 183. den v 11:57:36, od začátku roku je to 15 767 856 js.
Zimní obrat dle CET: 00:00:00 (+0,1 s), to je 31 536 000,1 s.
Zimní obrat dle SNST₉₁₁₅: 1. den roku v 00:00:00.
Prvý půlrok má 15 767 856 js, druhý půlrok má 15 768 144 ps.
SNST symetrie je částečně narušena. Sluneční rok zachovává 31 536 000 ss.

→

Letní obrat dle CET: 183. den v 10:31:08 (+0,95 s), od začátku roku je to 15 762 668,95 s.
Letní obrat dle SNST₉₁₁₅: 183. den v 12:02:24, od začátku roku je to 15 768 144 js.
Zimní obrat dle CET: 23:59:59 (+0,9 s), to je 31 535 999,9 s a 31.12.
Zimní obrat dle SNST₉₁₁₅: 1. den roku v 00:00:00.
Prvý půlrok má 15 768 144 js, druhý půlrok má 15 767 856 ps.
SNST symetrie je částečně narušena. Sluneční rok zachovává 31 536 000 ss.

SNST₇₃₁₂ a přestupný rok

←

Letní obrat dle CET: 183. den v 22:43:48 (+0,05 s), od začátku roku je to 15 806 628,05 s.
Letní obrat dle SNST₇₃₁₂: 183. den v 23:57:00, od začátku roku je to 15 811 020 js.
Zimní obrat dle CET: 00:00:00 (+0,1 s), to je 31 622 400,1 s.
Zimní obrat dle SNST₇₃₁₂: 1. den roku v 00:00:00.
Prvý půlrok má 15 811 020 js, druhý půlrok má 15 811 380 ps.
SNST symetrie je částečně narušena. Sluneční přestupný rok zachovává 31 622 400 ss.

→

Letní obrat dle CET: 183. den v 22:49:47 (+0,95 s), od začátku roku je to 15 806 987,95 s.
Letní obrat dle SNST₇₃₁₂: 184. den v 00:03:00, od začátku roku je to 15 811 380 js.
Zimní obrat dle CET: je 23:59:59 (+0,9 s), to je 31 622 399,9 s a 31.12.
Zimní obrat dle SNST₇₃₁₂: 1. den roku v 00:00:00.
Prvý půlrok má 15 811 380 js, druhý půlrok má 15 811 020 ps.
SNST symetrie je částečně narušena. Sluneční přestupný rok zachovává 31 622 400 ss.

SNST₉₁₃₀ a přestupný rok

←

Letní obrat dle CET: 183. den v 22:26:06 (+0,05 s), od začátku roku je to 15 805 566,05 s.
Letní obrat dle SNST₉₁₃₀: 183. den v 23:57:36, od začátku roku je to 15 811 056 js.
Zimní obrat dle CET: 00:00:00 (+0,1 s), to je 31 622 400,1 s.
Zimní obrat dle SNST₉₁₃₀: 1. den roku v 00:00:00.
Prvý půlrok má 15 811 056 js, druhý půlrok má 15 811 344 ps.
SNST symetrie je částečně narušena. Sluneční přestupný rok zachovává 31 622 400 ss.

→

Letní obrat dle CET: 183. den v 22:30:53 (+0,95 s), od začátku roku je to 15 805 853,95 s.
Letní obrat dle SNST₉₁₃₀: 184. den v 00:02:24, od začátku roku je to 15 811 344 js.
Zimní obrat dle CET: 23:59:59 (+0,9 s), to je 31 622 399,9 s a 31.12.
Zimní obrat dle SNST₉₁₃₀: 1. den roku v 00:00:00.
Prvý půlrok má 15 811 344 js, druhý půlrok má 15 811 056 ps.
SNST symetrie je částečně narušena. Sluneční přestupný rok zachovává 31 622 400 ss.

Po vložení malého časového intervalu do dříve navržených uzavřených cyklů se začátek dalšího roku (nový časový cyklus SNST) už nebude krýt se začátkem strojového cyklu (CET), ale bude posunut. Pravidelný posun obratu bude znamenat pravidelné posouvání začátku SNST vůči začátku CET.

Autor teorie i článku: Miloš Antes